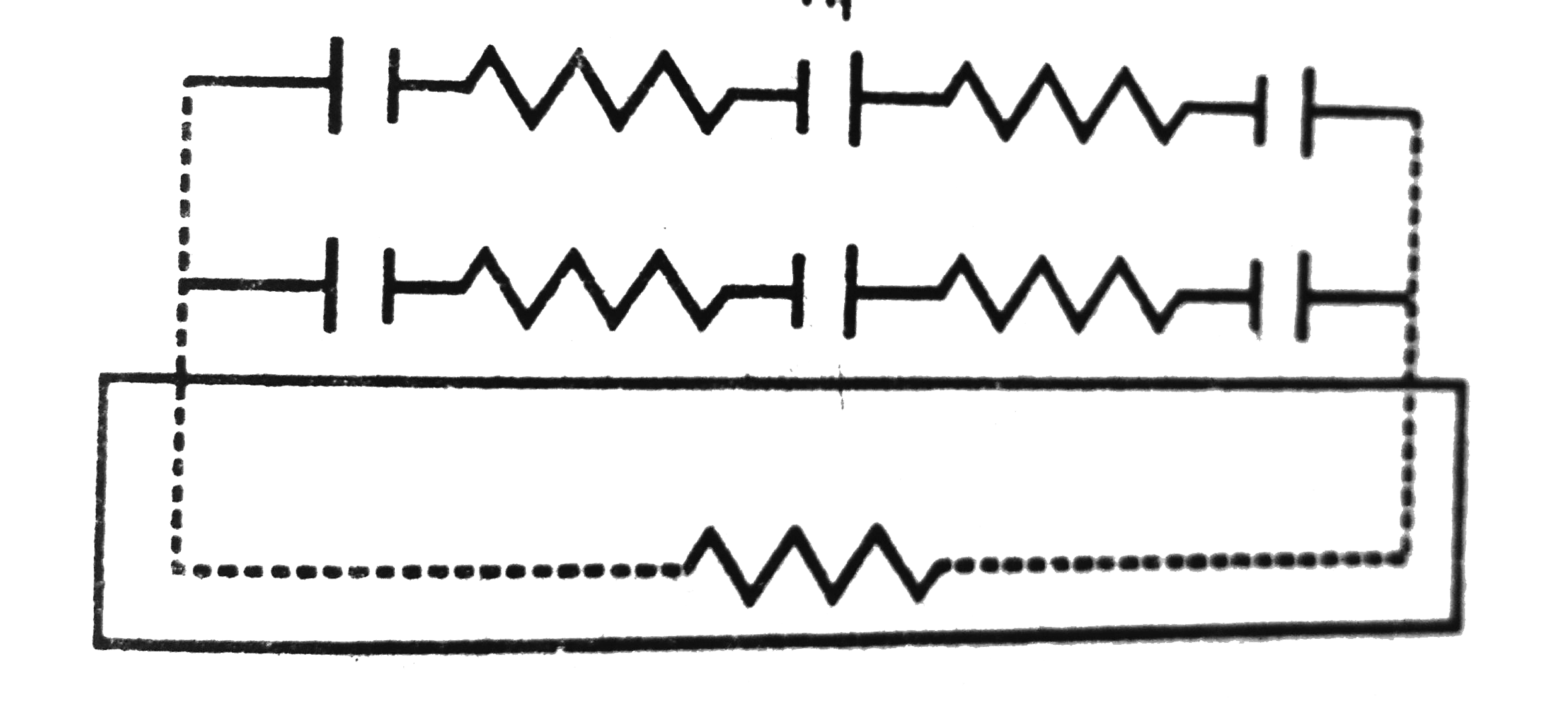
Consider $N = n_{1} n_{2}$ indentical cells, each of emf $(ε)$ and internal resistance r. Suppose $n_{1} c e l l s a r e j o \in e d \in s e r i e s \to f or n a l \in e and n_{2} s u c h a r e c o \cap e c t e d \in p a r a l \leq l . T h e c o m b \in a t i o n d r i v e s a c u r r e n t \in a n e x t e r n a l r e s i s tan c e R . (a) f \in d t h e c u r r e n t \in t h e e x t e r n a l r e s i s tan c e, (b) A s \sum \in g t ˆ$ n_(1) $and n_{2} c a n b e c o n t \in u o u s l y v a r i e d, f \in d t h e r e l a t i o n b e t w e e n$ n_(1) ,n_(2) R and r for which the current in R in maximum.

Text Solution

Verified by Experts

Total e.m.f. = $n_{1}$ E in one row
Total e.m.f. in all rows = $n_{1} E$
Total resistance in one row = $n_{1}$ r/ $n_{2}$
Net resistance = $R + (n_{1}) \frac{r}{n_{2}}$
$S o, C u r r e n t = R + ((n_{1}) \frac{r}{n_{2}})$
$(b) L = ((n_{1}) (n_{2}) \frac{E}{n_{2}} R + n_{2} r)$
For, L = max
$(n_{1}) r + (n_{2}) R = min i μ m$
$\Rightarrow {((\sqrt{n_{1}} r) - (\sqrt{n_{2}} R))}^{2} + 2 ((\sqrt{n_{1}} R (n_{2}) R)) = min .$
It is minimum when,
$(\sqrt{n_{1}} r) = (\sqrt{n_{2}} R)$
$n_{1} r = n_{2} R$
L is maximum when,
$n_{1} r = n_{2} R$ .

Updated on:21/07/2023

Four cell each of emf 2 V and internal resistance 1 ohm are connected n parallel with an external resistance of 6 ohm. The current in the external resistance is
A0.32 A
B0.16 A
C0.2 A
D0.6 A
n identical cells, each of emf e volt and internal resistance $r Ω$ are connected in a row m. Such rows are connected in parallel. This battery sends current through an external resistance R. The current will be maximum if

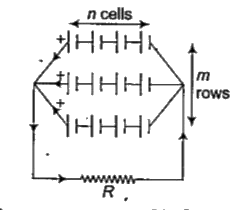Anr=mR
BnR=mr
Cnm=rR
DnmR=r
n identical cells, each of emf e volt and internal resistance $r Ω$ are connected in a row m. Such rows are connected in parallel. This battery sends current through an external resistance R. The current will be maximum if

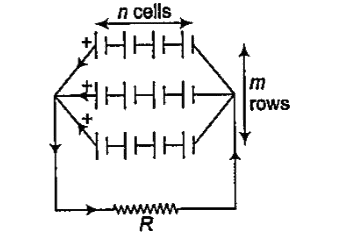Anr = mR
BnR = mr
Cnm = rR
DnmR = r