Shows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.

(a)The force on the wire due to the magnetic field is
→F=i→l×→B
or, F=ilB.
it acts towards right in the given figure. If the wire dose not slide on the rails, the force of freiction by the rails should be equal to F. If μ0 mg thus, μ0mg=ilB or, μ0=ilBmg (b) If the friction coefficient is μ=μ02=ilB2mg,thewirewillsl→wardsright.Theictionalforcebytherailsisf=mumg= (ilB)/(2)→wards≤ft.Therestant–––––forceisilB - (ilB)/(2)= (ilB)/(2)→wardsright.theae≤rationwillbea = (ilB)/(2) = (ilB)/(2)→wardsright.theae≤rationwillbea = (ilB)/(2m). The wire will slide towards right with this acceleration.
Topper's Solved these Questions
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Short Answer
10 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Objective 1
10 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- LIGHT WAVESBOOK - HC VERMACHAPTER - LIGHT WAVESEXERCISE - Exercises
41 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Exercises
61 Videos
Similar Questions
Figure shows a wire of resistance R sliding on two parallel, conducting fixed thick rails placed at a separation l. A magnetic fild B exist in a direction perpendicular to the plane of the rails. The wire is moving with a constant velocity v. Find current through the wire
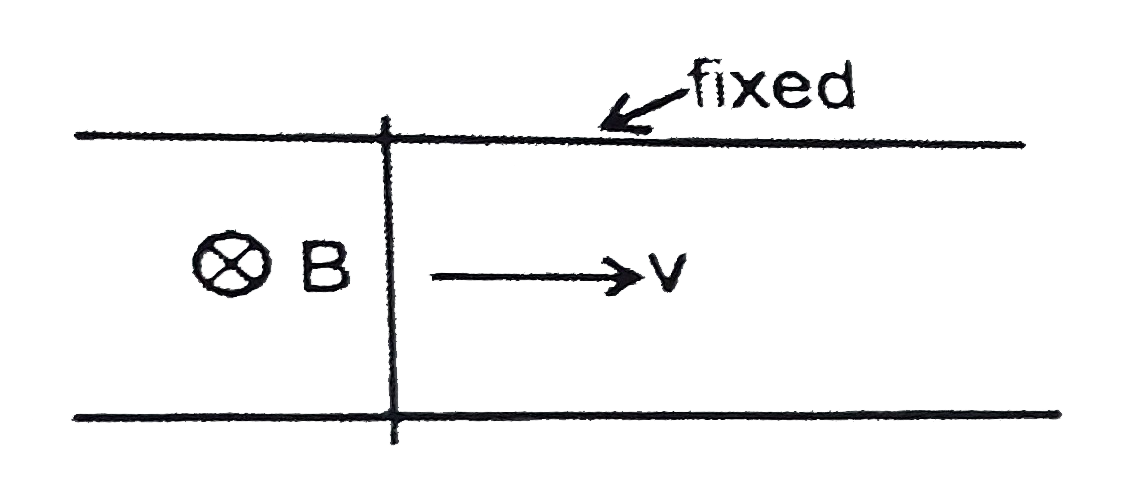
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View Solution
Knowledge Check
Figure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
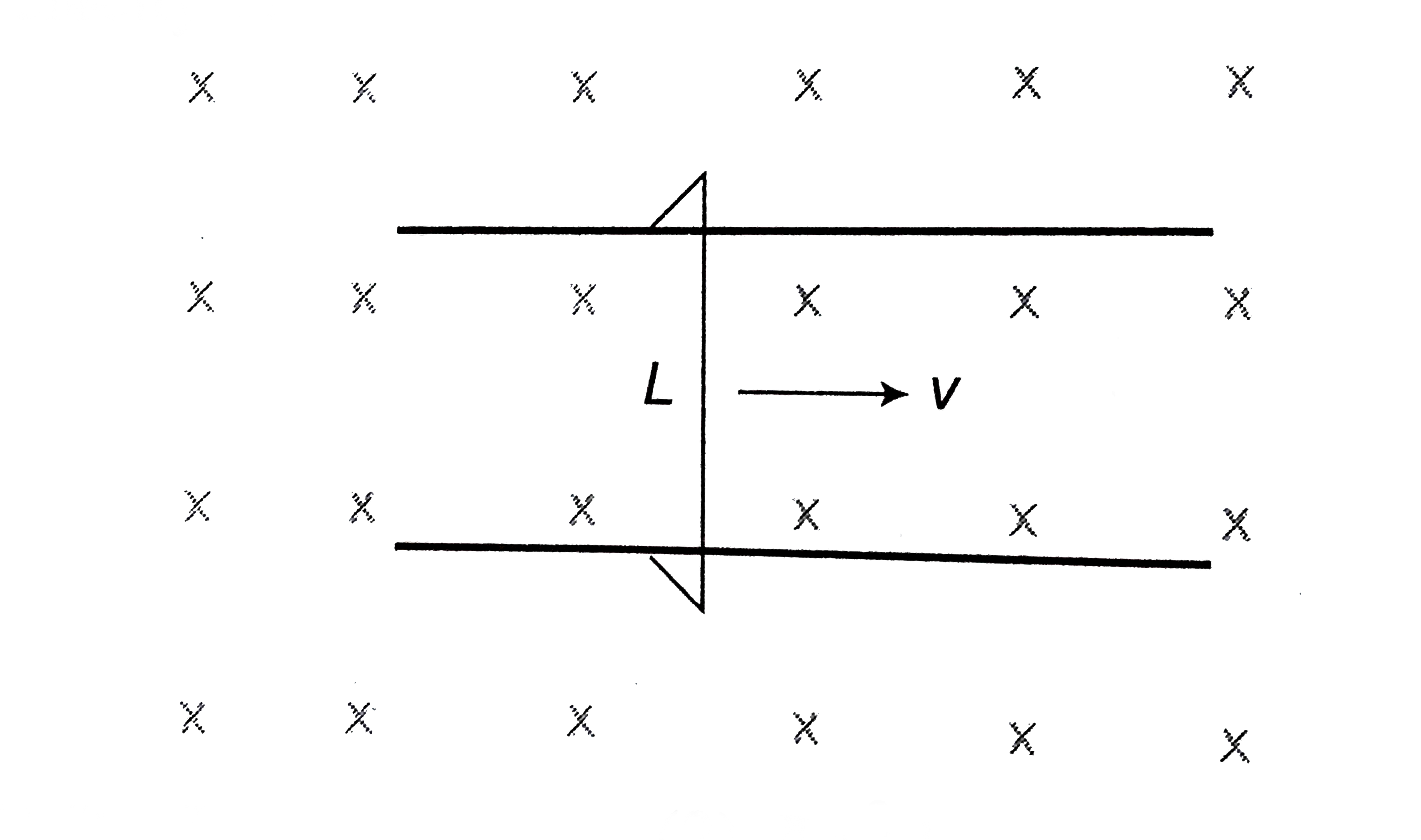 ABvLBBv2LCzeroDB2v2L/R
ABvLBBv2LCzeroDB2v2L/RA pair of long, smooth, parallel, horizontal, conducting rails are joined to a cell at one end. There are no external electric or magnetic fields. A metal rod is placed on the rails. The rod will
Aremain stationaryBmove towards the cellCmove away from the cellDoscillateA wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as
 Aa=C2B2l−FmBa=Fm+CBlCa=FC2B2lmDa=Fm+C2B2l
Aa=C2B2l−FmBa=Fm+CBlCa=FC2B2lmDa=Fm+C2B2l
A copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is μs What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
View SolutionTwo long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.

A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The current in the wire MN is
View SolutionTwo long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.

A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The force required to pull the ring with uniform velocity v is
View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
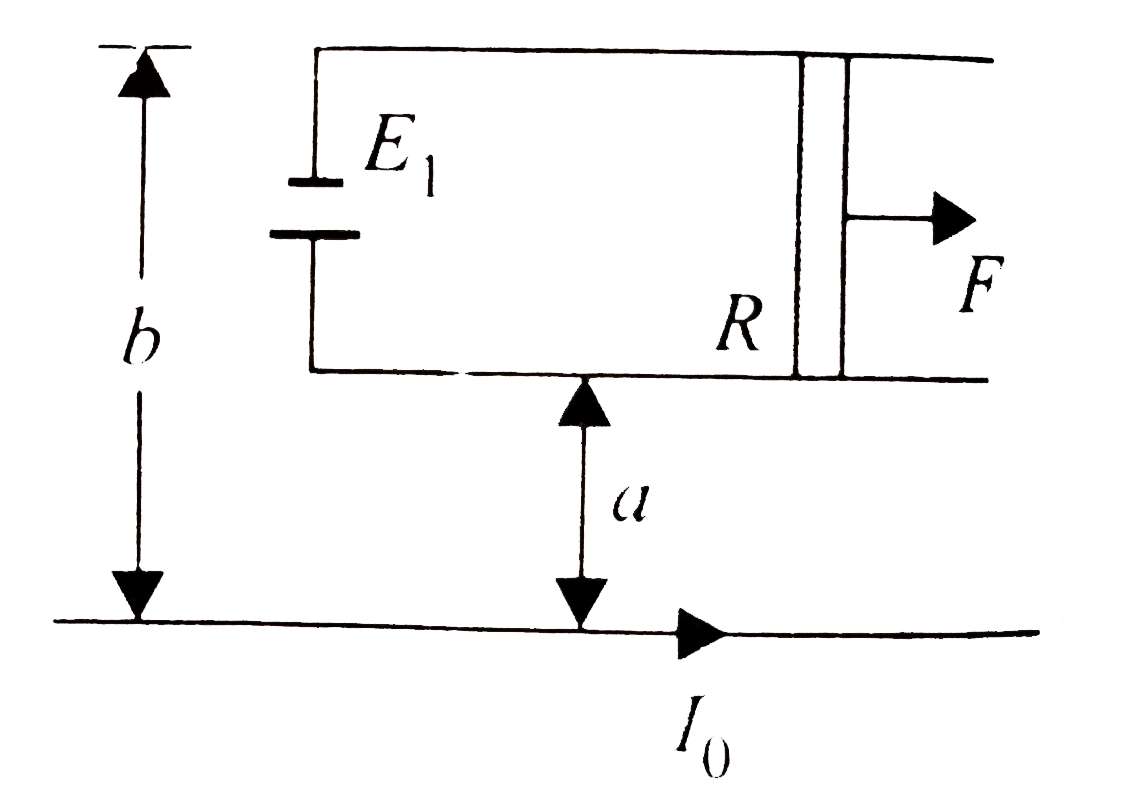
Find the value of current in the circuit if the rod slides with constant velocity v0
View SolutionA conductor bar with mass m and length L slides over horizontal rails that are connected to a voltage source. The voltage source maintains a constant current I in the rails and bar, and constant, uniform, vertical magnetic field →B fills the region between the rails (as shown in Fig.)

If the bar has mass m, find the distance d that the bar must move along the rails from rest to attain speed v.
View Solution
