Two long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.

A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The force required to pull the ring with uniform velocity v is
4B2vd3πλ
3B2vd4πλ
2B2vd3πλ
4B2vdπλ
The correct Answer is:D
When ring moves to the right, emf is induced in each of the two semi-circles. During an elemental time interval dt, displacment of the ring is v dt.
Consider tow semi-circular separately.
During this interval, left semi-circle cuts flux area shown as shaded part in fig. This area is d (v dt). Therefore, flux cut by semi-circle during this interval is,
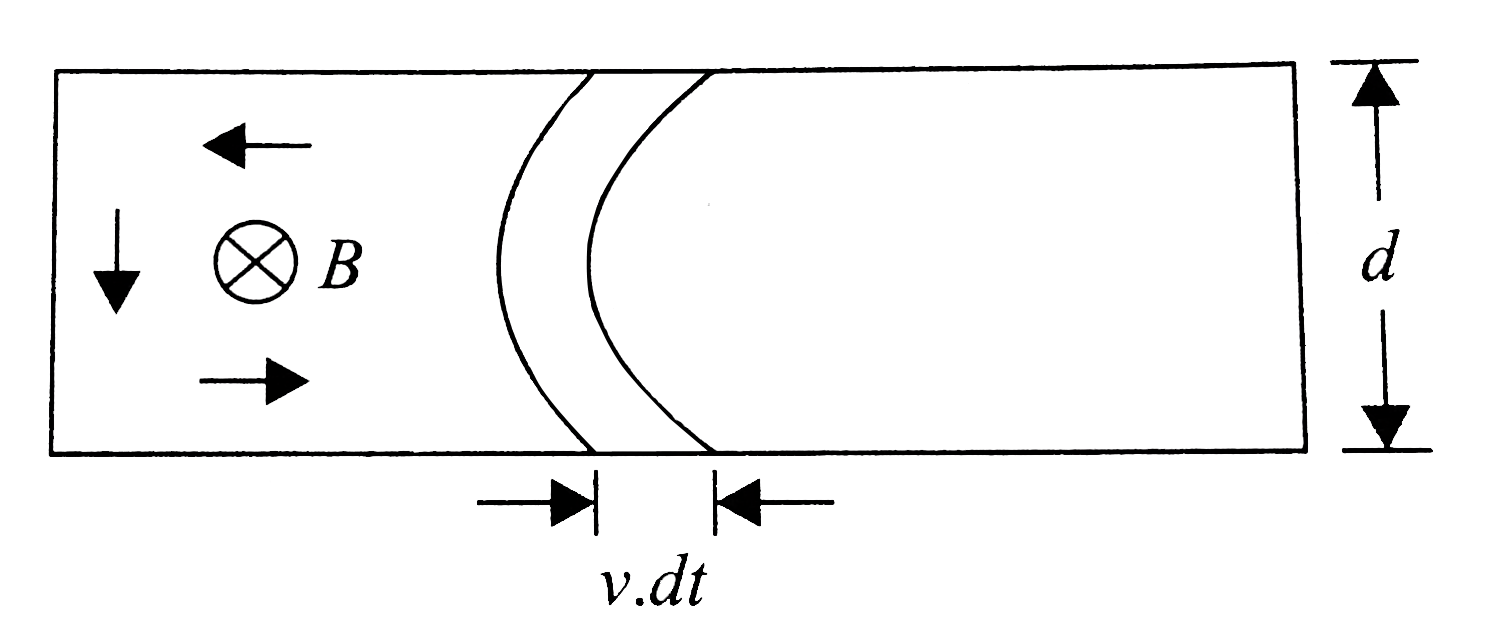
dϕ=Bd(vdt)
Hence, emf induced in it is e=dϕdt=Bvd
This emf tries to force an anticlockwise current in the circuit as shown in fig.
Similarly, emf induced in right semi-circle is also equal to e=Bvd and it also tries to force current in the same direction as shown in fig.
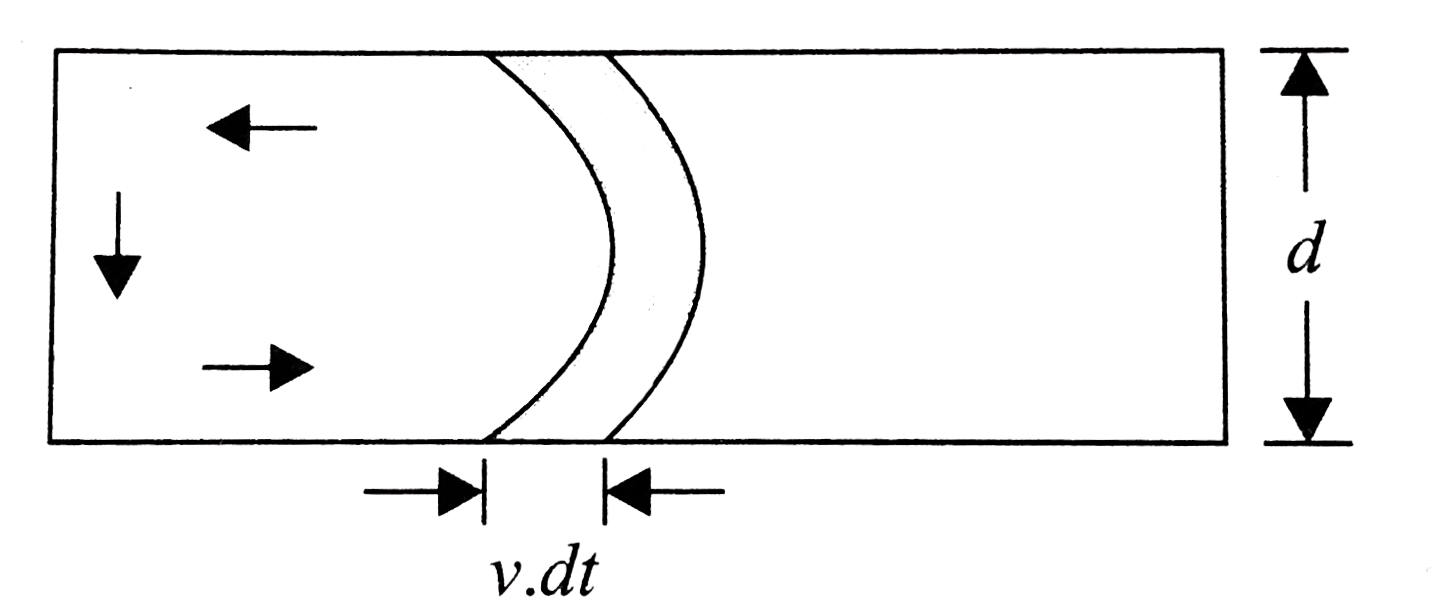
Hence , these tow semi-circles are two identicla electrical sources connected in parallel with each other. EMF of each source is e=Bvd and internal resistance is, r=(πd/2)λ.
∴ Equivalent internal resistance of parallel combination of two source is
r2=14πdλ
Since, rails have negligible resistance, therefore, equivalent resistance of the circuit is,
R=r2=14πλd
Hence induced current through rails is
l=eR
But current through each semi-circle is equal to I/2.
Force required to maintain velocity of ring at constant = Retarding force acting on ring due to induced current = 2 X Retarding force on each semi-circle. ltbr> 2×B12d=Bld=4B2vdπλ.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- Moving charges and magnetismBOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20 Videos
Similar Questions
Shows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.

View SolutionTwo parallel fixed conducting rails are l distance apart. They are connected by a conducting wire xy. A uniform magnetic field B is applied normal to its plane. Two other rods PQ and RT(RS = ST) are moved with a constant velocity v. Resistance/ length of these two rods are λ no other wire has resistance. Then :

View Solution
Knowledge Check
Two long parallel conducting horizontal rails are connected by a conducting wire at one end. A uniform magnetic field B (directed vertically downwards) exists in the region of space.

A light uniform ring of diameter d which is practically equal to separation between the rails is placed over the rails as shown in Fig. If resistance of ring be (λ) per unit length
The current in the wire MN isA2Bv3πλ from M to NBBv3πλ from M to NC2Bv3πλ from N to MDNone of theseTwo long parallel conducting wires carry current I in same direction, placed at distance b. Force per unit length of wire is
Aμ0I2πbBμ0I22πb2Cμ0I22πbDμ0I2πb2A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
AIt is rotated about it axisBit is translatedCit is rotated about a diameterDit is deformed
A long conducting wire AH is moved over a conducting triangular wire CDE with a constant velocity v in a uniform magnetic field →B directed into the plane of the paper. Resistance per unit length of each wire is ρ. Then
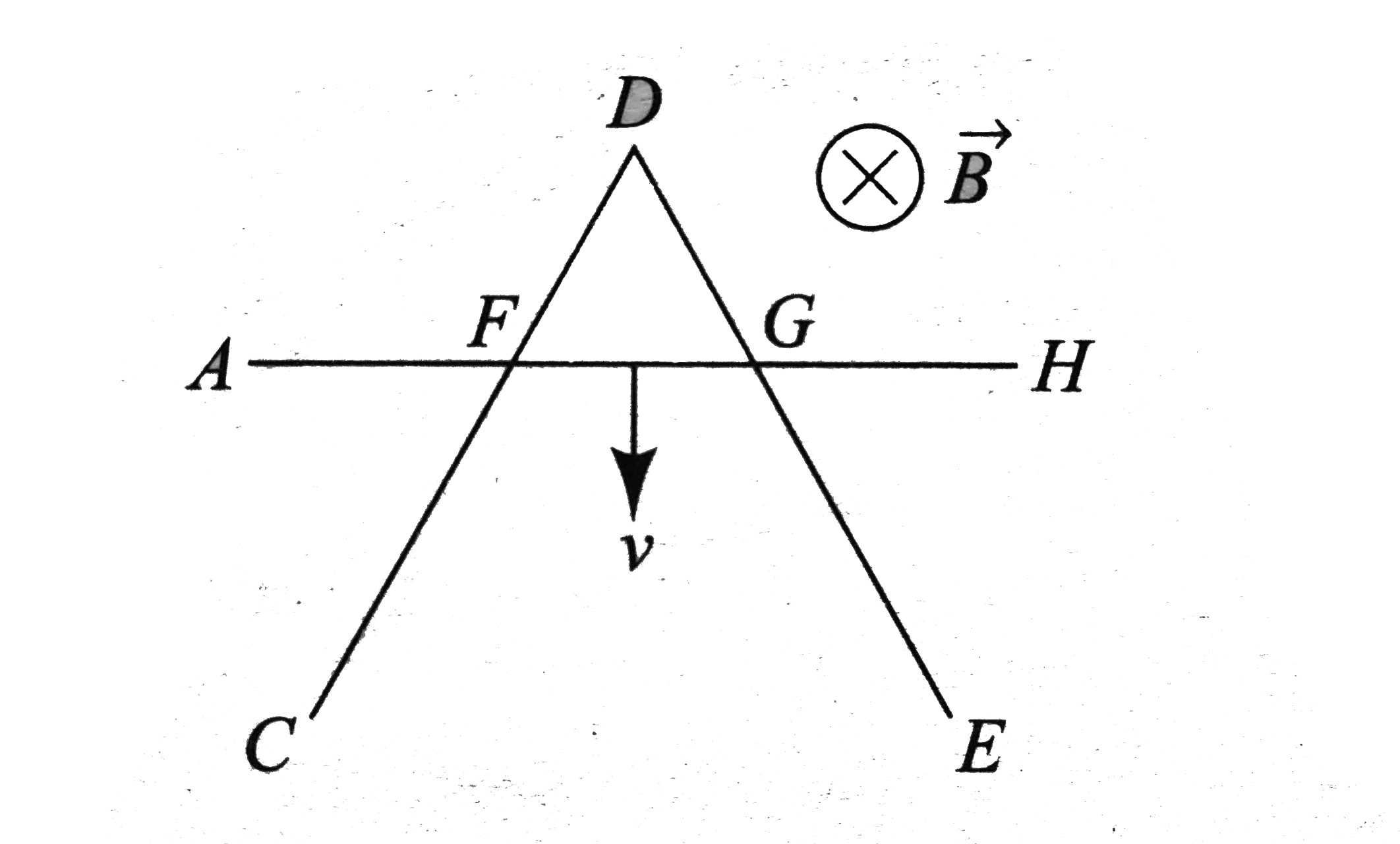
View SolutionA pair of long, smooth, parallel, horizontal, conducting rails are joined to a cell at one end. There are no external electric or magnetic fields. A metal rod is placed on the rails. The rod will
View SolutionTwo parallel resistanceless rails are connected by an inductor of inductance L at one end as shows in Fig. A magnetic field B exists in the space which is perendicular to the plane of the rails. Now a conductor of length l and mass m is placed transverse on the rail and given an inpulse J toward the rightward direction. Then choose the correct option (S).
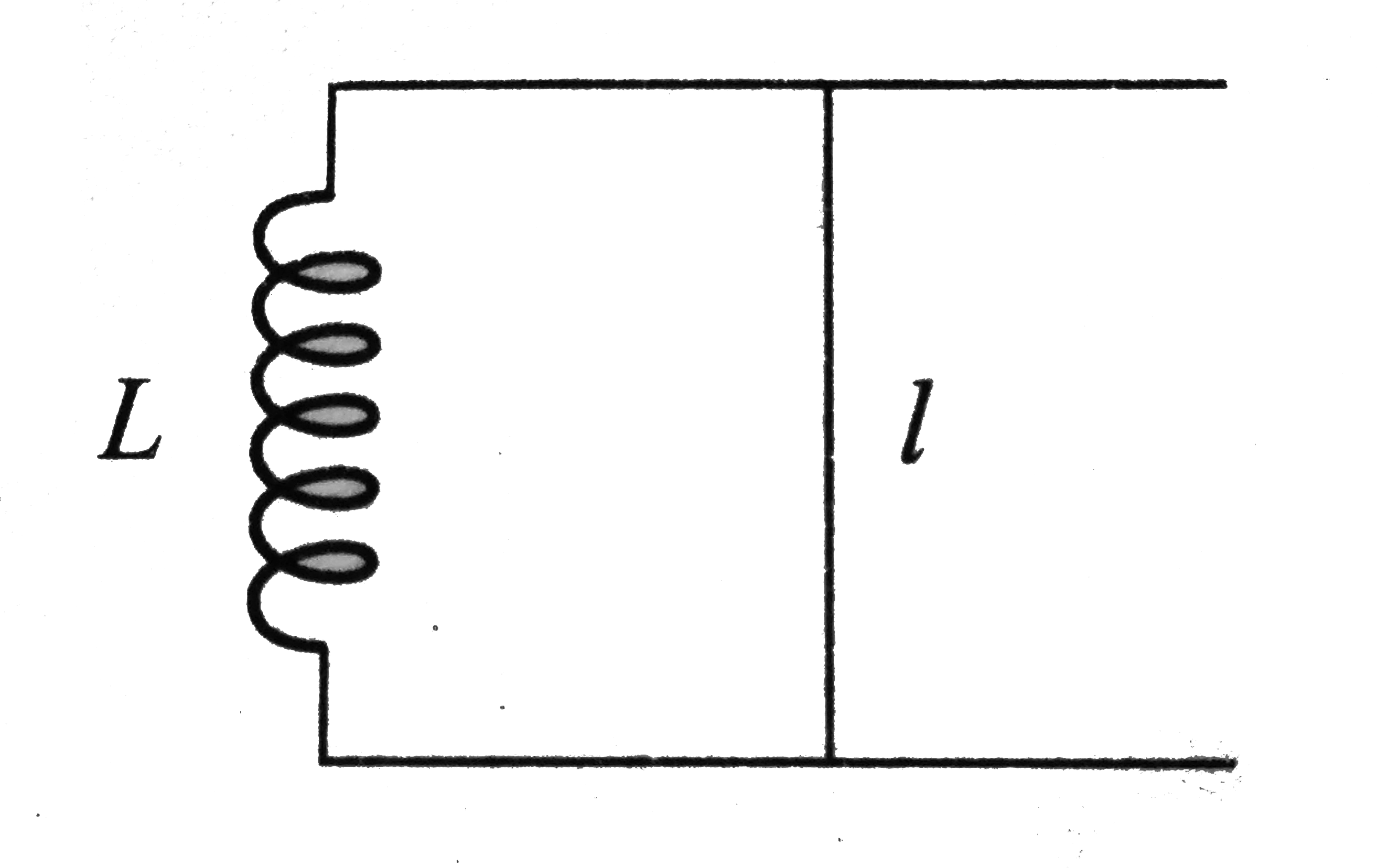
View SolutionTwo parallel resistanceless rails are connected by an inductor or inductance L at one end as shown in figure. A magnetic field B exists in the space which is perpendicular to the plane of the rails. Now a conductor of length l and mass m is placed transverse on the rail and given an impulse J towards the rightward direction. Then select the corrent option(s).
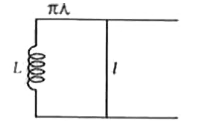
View SolutionA pair of parallel conducting rails lie at right angle to a uniform magnetic field of 2.0T as shown in the fig. two resistor 10Ω and 5Ω are to slide without friction along the rail. The distance between the conducting rails is 0.1m. Then

View Solution
