Suppose that the radius of cross section of the wire used in the previons problem is r. Find the increase in the radius of the loop if the magnetic field is switched off. The young modulus of the material of the wire is Y.
Wthe the magnetic field is swiched the tension increase . The lenth of wire .
Y=(TA)/(ΔlL)
orAL=TITA=(iaB)/(Yπr2
2π×Δr=(iaB2πa)/(Yπr2) .
Topper's Solved these Questions
Similar Questions
Suppose that the radius of cross-section of the wire used in the previous problem is 2.the decreases in the radius of the loop is ia2BNπY if the magnetic field is swithed off.The Young's modulus of the material of the wire is Y.Then find value of N.
View SolutionA wire of length l and cross-sectional are A is suspended at one of its ends from a ceiling. What will be its strain energy due to its own weight, if the density and Young's modulus of the material of the wire be d and Y?
View Solution
Knowledge Check
As temperture increases the Young's modulus of the material of a wire
AincreasesBdecreasesCremains the sameDbecomes infiniteIn the experiment to determine Young's modulus of the material of a wire under tension
used in the arrangement as shown. The percentage error in the measurement
of length is a in the measurement of the radius of the wire is b and in the
measurement of the change in length of the wire is c. Percentage error in the measurement
of Young's modulus for a given load is
 Aa−2b+cBa−2b−cCa+2b+cDa+2b
Aa−2b+cBa−2b−cCa+2b+cDa+2bA thin wire of cross section a is made to from a flexible circular loop of radius R. If the loop spins with angular speed ω, the (Assume ρ = density and y = Young's modulus fo wire)
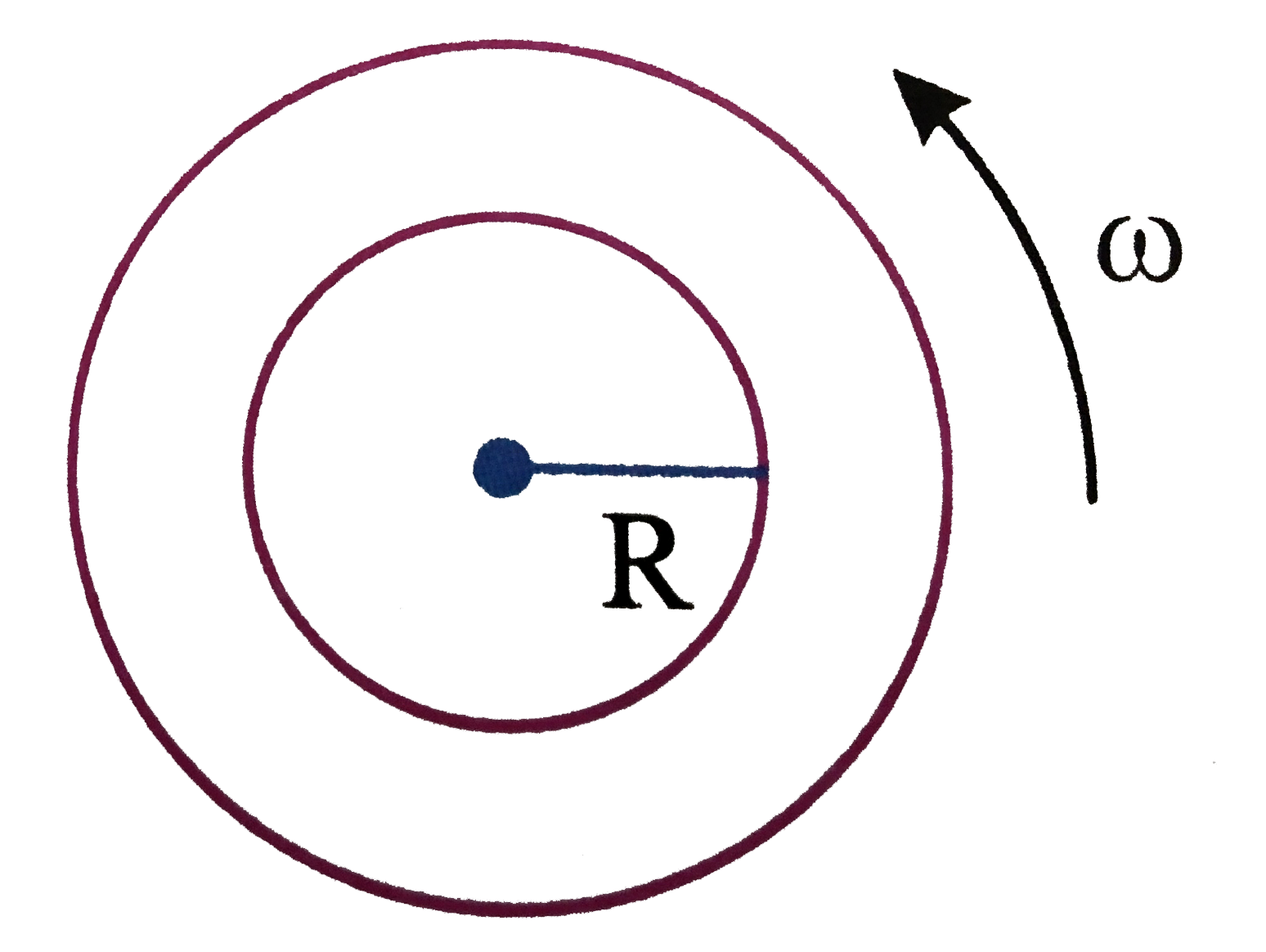
Stress in the wire isAρR2ω2BρRωCR2ω2ρDR2ω22ρ
A force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionA bar of mass m and length l is hanging from point A as shown in figure. Find the increase in its length due to its own weight. The young's modulus of elasicity of the wire is Y and area of cross-section of the wire is A.

View SolutionA thin wire of cross section a is made to from a flexible circular loop of radius R. If the loop spins with angular speed ω, the (Assume ρ = density and y = Young's modulus fo wire)

Tension in the wire is
View SolutionA wire carrying current i is shaped as shown. Section AB is a quarter circle of radius r. The magnetic field is directed
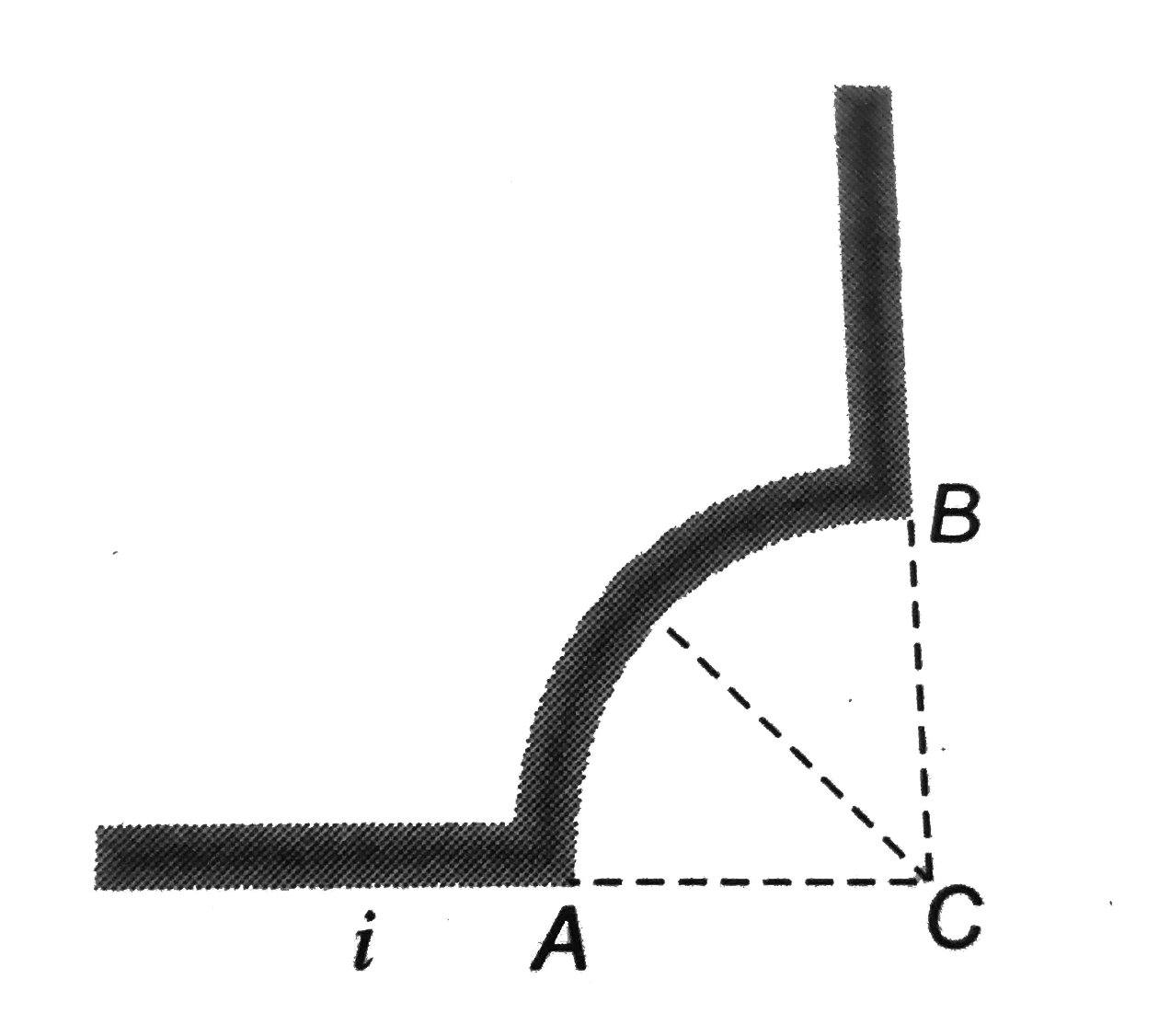
View SolutionThe correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
View Solution
