Consider the situation of the previous problem. A particle having charge q and mass m is projected from the point Q in a direction going into the plane of the diagram. It is found to describe a circle of radius r between the two plates. Find the speed of the charged particle.
Given charge =q
and mass= m radiu = r
We know that,
Radius descirbed by a charged particle in
a magnetic field
r=mvqB
⇒v=Bqrm=μokqrm
[using Ampere's circuital law]
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
There is one long solenoid with turns per unit length. The radius of the solenoid is R and current flowing through it is I. There is a charged particle having charge q and mass m projected from a point on axis of the solenoid, and in a direction perpendicular to the axis. Find the maximum possible speed with which the charged particle can be projected so as not to strike the solenoid.
View SolutionConsider the situation described in the previous example. A particle of mass m having a charge q is placed at a distance d from the metal sheet and is projected towards it. Find the maximum velocity of projection for which the particle does not hit the sheet.
View Solution
Knowledge Check
Two charged particles each having a charge +q and mass m are kept at a distance d. if they are in equilibrium under the gravitational force and the electric force between them, then the ratio qm or specific charge of each particle is
A√4πε0GB√4πε0GC4πε0GDG4πε0A charged particle of mass m is moving with a speed u in a circle of radius r. If the magnetic field induction at the centre is B, the charge on the particle is
A4πr2Bμ0uB2πr2Bμ0uCmuBrD2muBrA particle of mass m and positive charge q is projected with a speed of v0 in y–direction in the presence of electric and magnetic field are in x–direction. Find the instant of time at which the speed of particle becomes double the initial speed.
A√3mv0qEB√2mv0qECmv0qED√3mv02qE
A tightly-wound, long solenoid has n turns per unit length, a radius r and carries a current i. A particle having charge q and mass m is projected from a point on the axis in a direction perpendicular to the axis. What can be the maximum speed for which the particle does not strike the solenoid?
View Solution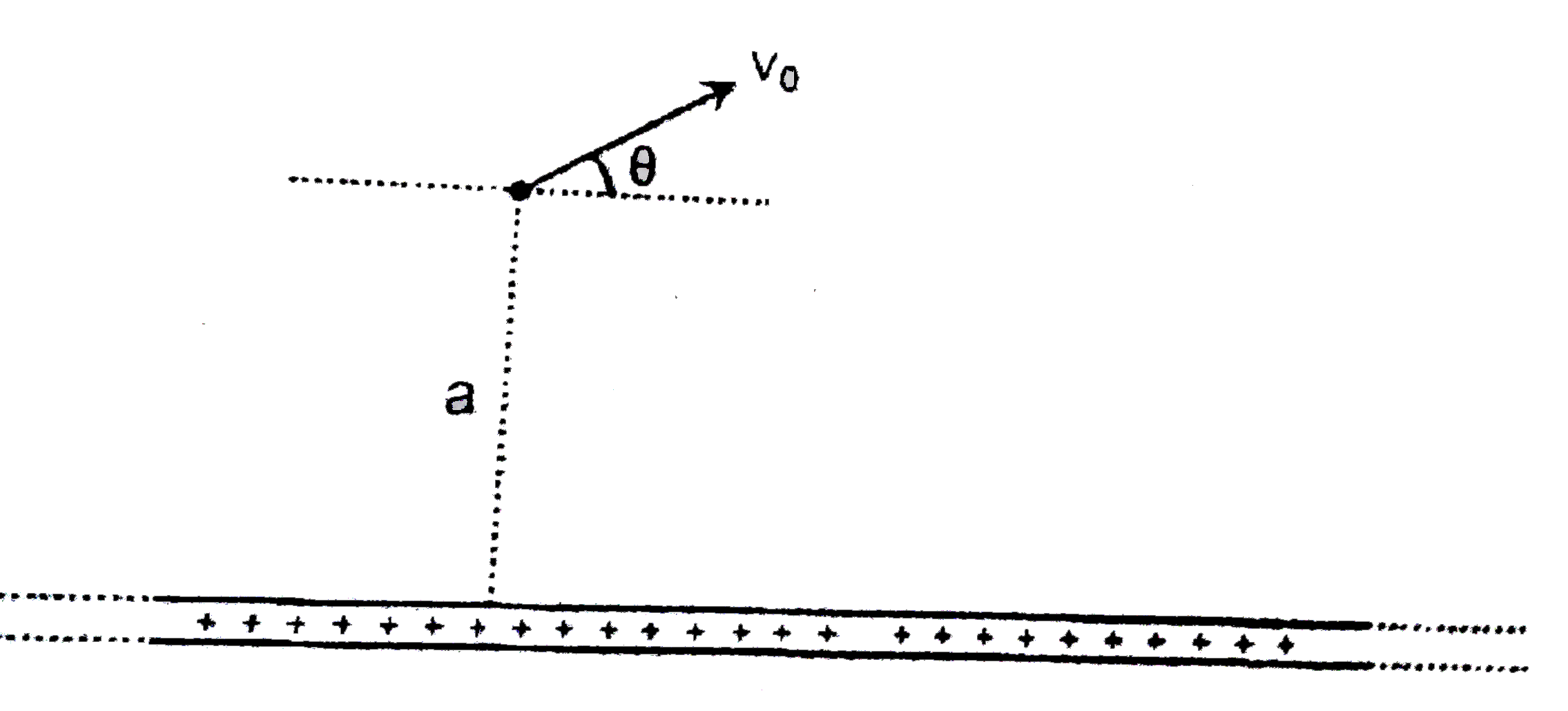
There is an infinite line of uniform linear density of charge +λ. A particle of charge −q & mass m is projected with initial velocity v0 at an angle θ with the line of charge from a distance a from it. The point charge moves in plane containing line charge and point of projection The speed of the particle of found to be minimum when it's distance from the line of charge is ae(nπmε200/qλ). The value of n is (ingnore gravity)
View SolutionFind the angular momentum of a particle of mass m describing a circle of radius r with angular speed ω.
View SolutionIn the fig shown XX represents a vertical plane perpendicular to the plane of the fig. To the right of this plane there is a uniform horizontal magnetic field B directed into the plane of the fig. A uniform electric field E exists horizontally perpendicular to the magnetic field in entire space. A charge particle having charge q and mass m is projected vertically upward from point O. It crosses the plane XX after time T. Find the speed of projection of the particle if it was observed to move uniformly after time T. It is given that qE = mg.
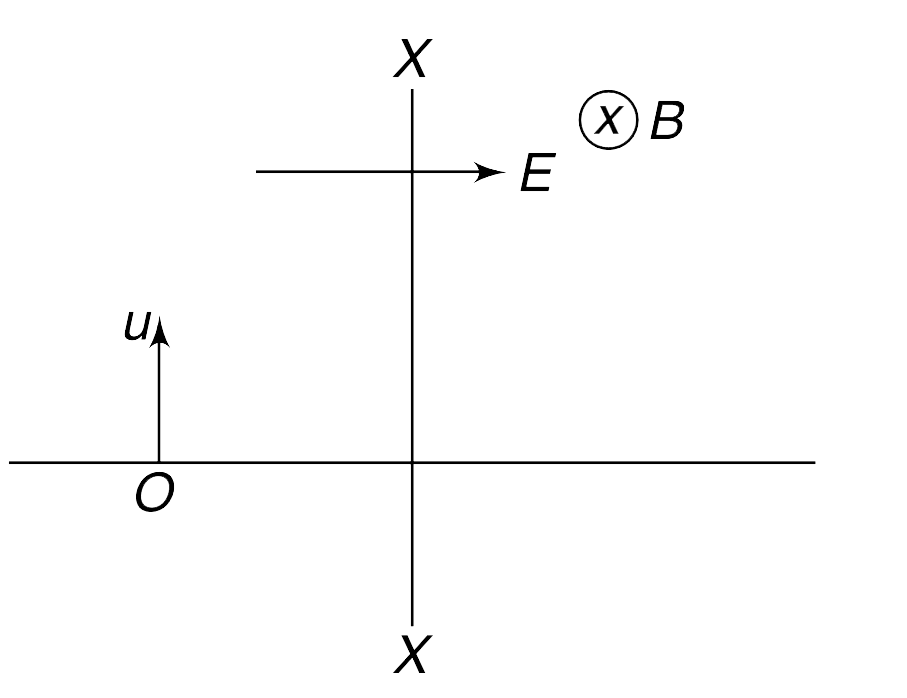
View SolutionA particle is having mass m & charge +q is projected horizontally from point O. Electric field is present and is directed vertically downward .
View Solution
