Twenty meters of wire is available for fencing a flower -bed in the form of a circular sector .Then the maximum area in square meters of the flower bed is
12.5
10
25
30
The correct Answer is:C
Let r be the radius and θ ( in radians ) be the sector angle of the circular sector. Further let A be the area of the sector . Then
A=12r2θ

If is given that perimeter of the sector of the of OAB is 20 meters
∴r+rθ=20⇒=20−2rr
From (i) and (ii) we obtain
A=12r2(20−2rr)≠10r−r2
⇒dAdr=10−2randd2Adr2=−2
For maximum and minimum values of A we must have
dAdr=0⇒10−2r−0⇒=5
Putting r=5 in (ii) we obtain θ=2
∴A=12×52×2=25m2
Topper's Solved these Questions
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMACHAPTER - MAXIMA AND MINIMA EXERCISE - Section I - Solved Mcqs
72 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMACHAPTER - MAXIMA AND MINIMA EXERCISE - Section II - Assertion Reason Type
7 Videos
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMACHAPTER - MATHEMATICAL REASONING EXERCISE - Chapter Test
20 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - OBJECTIVE RD SHARMACHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test
21 Videos
Similar Questions
Knowledge Check
Find the volume of a cube whose surface area is 54 square meter
A27m3B9m3C163D81m3
Find the area of the flower bed (with semicircular ends).

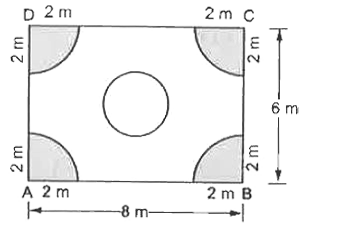
View SolutionIn each of the corners, there is a flower bed in the form of a quadrant of a circle of radius 2 m. Also, there is a flower bed in the form of a circle of radius 2 m in the middle of the plot. Find the area of the remaining plot.
View SolutionThere are two circular flower beds on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
View SolutionIn Figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawns and the flower beds.
View SolutionFind the area of the flower bed (with semi-circular ends) shown in figure

View SolutionEach side of a square park is 80 m. At each corner of the park there is a flower bed in the form of a quadrant of a circle of radius 14 m, as shown in the figure. Find the area of the remaining part of the park.
View SolutionThe cost of fencing a circular field at the rate of Rs 25 per meter is Rs 5,275 . Find the diameter of the field.
View Solution

