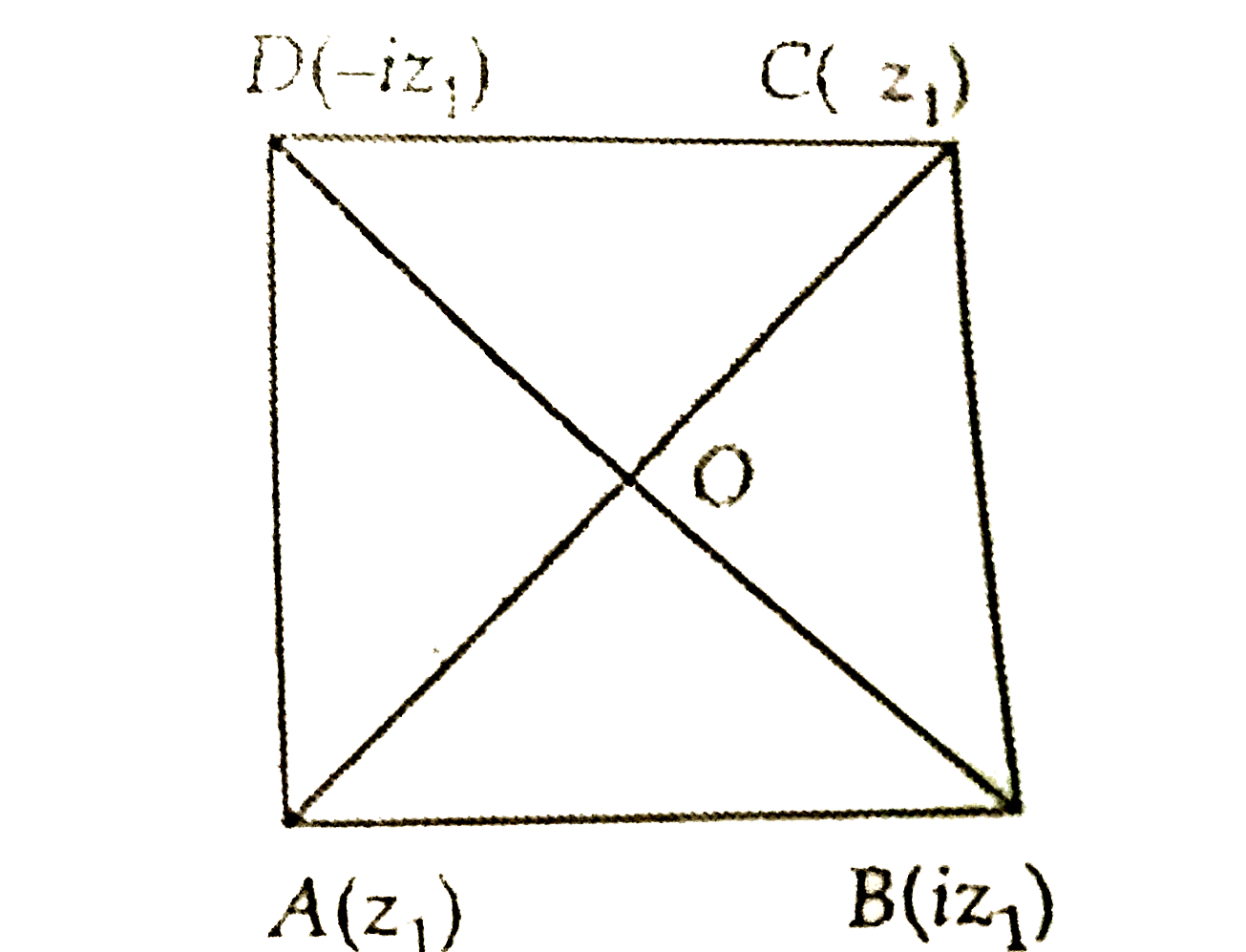
The center of a square ABCD is at the origin and point A is reprsented

The center of a square ABCD is at z=0. The affix of the vertex A is $z_{1}$ . Then, the affix of the centroid of the triangle ABC is
A $z_{1} (cos π \pm i sin π)$
B $\frac{z_{1}}{3} (cos π \pm sin π)$
C $z_{1} (cos (\frac{π}{2}) \pm sin (\frac{π}{2}))$
D $\frac{z_{1}}{3} (cos (\frac{π}{2}) \pm sin (\frac{π}{2}))$
The centre of a square ABCD is at z=0, A is $z_{1}$ . Then, the centroid of $△ A B C$ is (where, $i = \sqrt{- 1}$ )
A $z_{1} (cos π \pm i sin π)$
B $\frac{z_{1}}{3} (cos π \pm i sin π)$
C $z_{1} (cos (\frac{π}{2}) \pm i sin (\frac{π}{2}))$
D $\frac{z_{1}}{3} (cos (\frac{π}{2}) \pm i sin (\frac{π}{2}))$
The point of intersection of diagonals of a square ABCD is at the origin and one of its vertices is at a(4,2). What is the equation of the diagonal BD?
A $2 x + y = 0$
B $2 x - y = 0$
C $x + 2 y = 0$
D $x - 2 y = 0$

The center of a square ABCD is at the origin and point A is reprsented by $z_{1}$ . The centroid of $△ B C D$ is represented by