Let $O$ , $A$ , $B$ be three collinear points such that $O A . O B = 1$ . If $O$ and $B$ represent the complex numbers $O$ and $z$ , then $A$ represents

$\frac{1}{z}$

$¯ z$

$\frac{1}{¯ z}$

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Let OP.OQ=1 and let O,P and Q be three collinear points. If O and Q represent the complex numbers of origin and z respectively, then P represents
A $\frac{1}{z}$
B $¯ z$
C $\frac{1}{¯ z}$
D $- z$
Let A,B,C be three collinear points which are such that AB.AC=1 and the points are represented in the Argand plane by the complex numbers, 0, $z_{1}$ and $z_{2}$ respectively. Then,
A $z_{1} z_{2} = 1$
B $z_{1} {¯ z}_{2} = 1$
C $| z_{1} | | z_{2} | = 1$
D $z_{1} = {¯ z}_{2} ∣$
In a given parallelogram, if the points $P_{1}$ and $P_{2}$ represent two complex numbers $z_{1}$ and $z_{2}$ , then the point $P_{3}$ represents the number
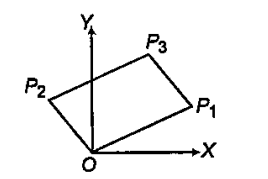A $z_{1} + z_{2}$
B $z_{1} - z_{2}$
C $z_{1} \times z_{2}$
D $z_{1} + z_{2}$