If z1 and z2 are lying on |z−3|≤4 and |z−1|=|z+1|=3 respecively. Then d=|z1−z2| satisfies.
A
0≤d<152
B
0<d≤152
C
0≤d≤172
D
0<d<172
Video Solution
Text Solution
The correct Answer is:C
P(z1) and Q(z2) are points on the circle |z−3|≤4 and the ellipse |z−1|=|z+1|=3 respectively. The center of the circle is at (3,0) and radius 4. The center of the ellipse is at the origin and foci at S(1,0) and S′(−1,0). The major axis ∀′ is of length 3. Therefore, OA= OA′=32.
Clearly, d=PQ. The minimum value of d is 0 when P and Q coincide with L or M.
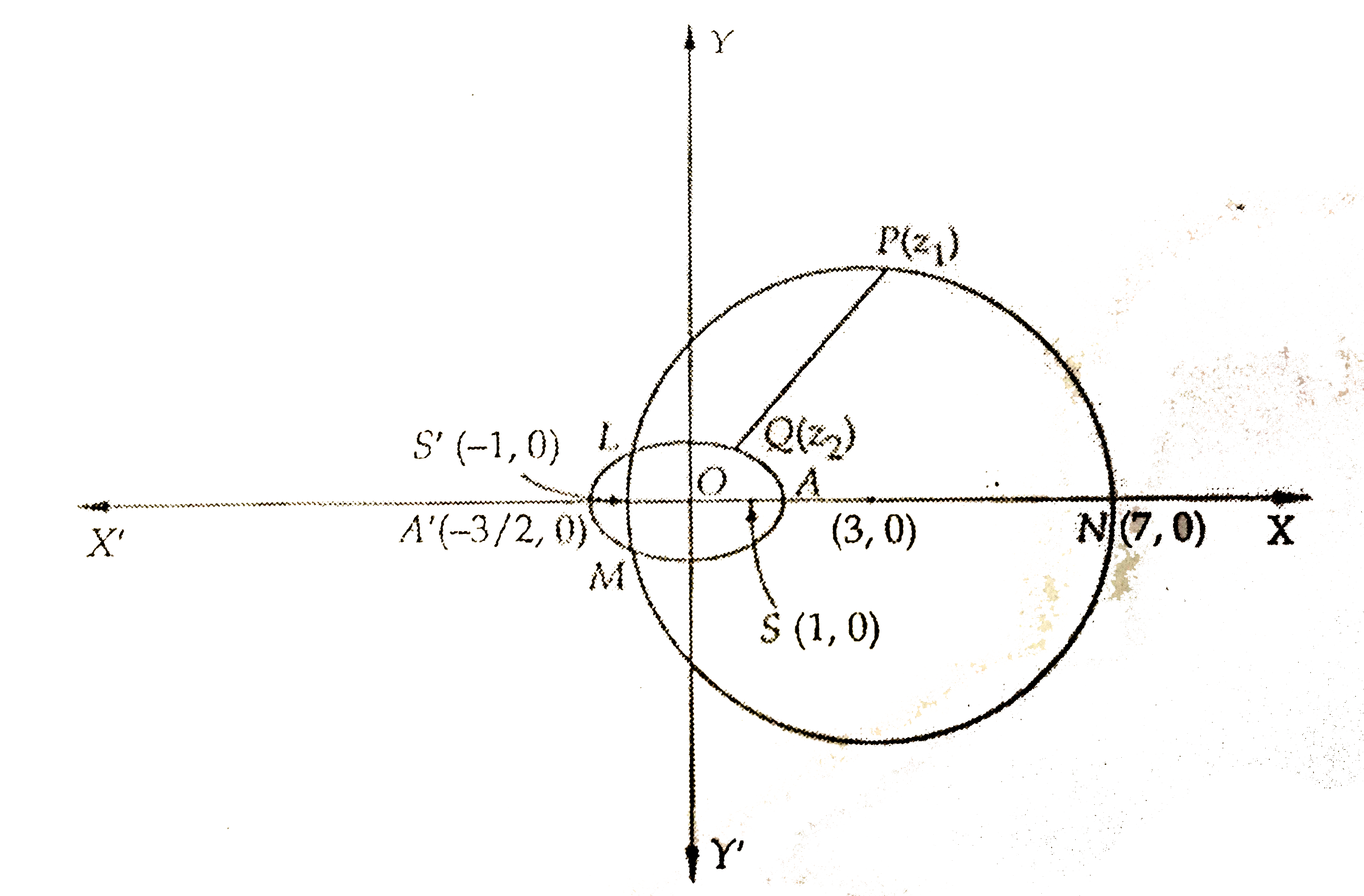
The maximum value of PQ is
A′N=OA′+ON=32+7=172
Hence, 0≤d≤172.
|
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Exercise
131 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
Similar Questions
Knowledge Check
For all complex numbers z1,z2 satisfying |z1|=12 and |z2−3−4i|=5, find the minimum value of |z1−z2|
A0B2C7D17If z1 and z2 satisfy the equation 2|z+3|=|Re(z)| and argz+31+i=π2, then arg z1+3z2+3 is equal to
A0B±π2C±πD±π4Let z1,z2,z3,z4 are distinct complex numbers satisfying |z|=1 and 4z3=3(z1+z2), then |z1−z2| is equal to
A1 or iBior−iC1 or iDior−1
If z1andz2 both satisfy the relation z+¯z=2|z−1|andarg(z1−z2)=π4, then Im(z1+z2) equals
View Solutionz1,z2 satisfy |z–8|=3andz1z2 is purely real and positive then |z1z2|=
View SolutionLet z1,z2 be two complex numbers satisfying the equations ∣∣∣z−4z−8∣∣∣=1and∣∣∣z−8iz−12∣∣∣=35, then √|z1−z2| is equal to __________
View SolutionFor all complex numbers z1,z2 satisfying |z1|=12 and |z2−3−4i|=5, find the minimum value of |z1−z2|
View SolutionIf z1,z2,z3 are three points lying on the circle |z|=2, then minimum value of |z1+z2|2+|z2+z3|2+|z3+z1|2=
View Solution
