The maximum area of the triangle formed by the complex coordinates z,z1,z2 which satisfy the relations |z−z1|=|z−z2| and ∣∣∣z−z1+z22∣∣∣≤r,where r>|z1−z2| is
A
12|z1−z2|2
B
12|z1−z2|r
C
12|z1−z2|2r2
D
12|z1−z2|r2
Video Solution
Text Solution
The correct Answer is:B
Let A(z), B(z1) and C(z2) be the points forming triangle ABC.
It is given that,
|z−z1|=|z−z2|
⇒ AB=AC
⇒ A lies on or the perpendicular bisector of BC.
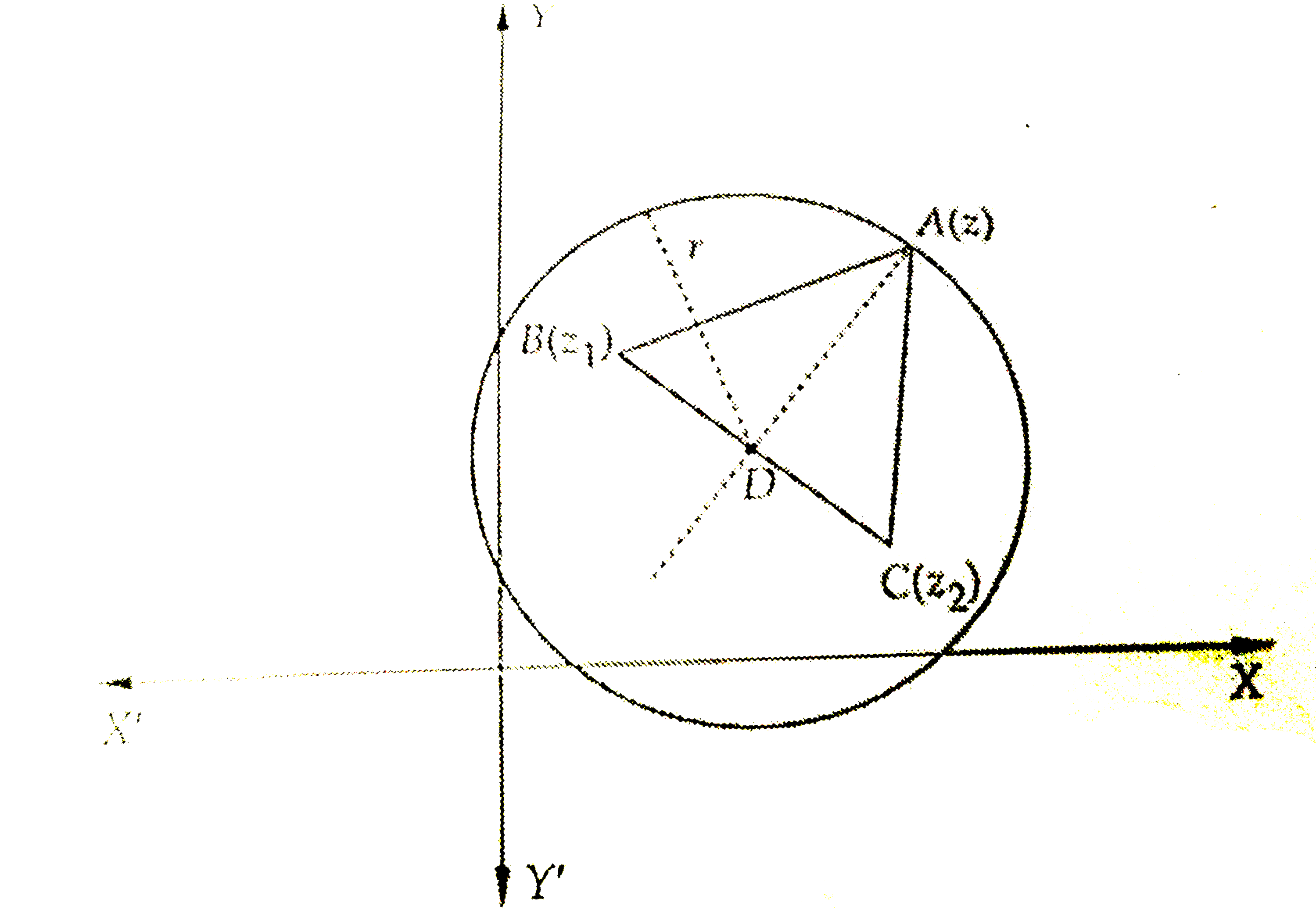
Also,
∣∣∣z−z1+z22∣∣∣≤r
⇒ A(z) lies on or interior of the circle having center at the mid-points of BC and radius r(>BC)
Now, Area of △ABC.
12(BC×AD)=12|z1−z2|∣∣∣z−z1+z22∣∣∣≤12|z1−z2|r.
Hence, the maximum area of △ABC is 12|z1−z2|r.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type15videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Exercise131videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test59videos
COMPLEX NUMBERS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test55videos
CIRCLES
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One
If z1≠−z2 and |z1+z2|=∣∣∣1z1+1z2∣∣∣ then :
Aat least one of z1,z2 is unimodularBboth z1,z2 are unimodularCz1.z2 is unimodularDz1−z2 is unimodular - Question 2 - Select One or More
Let two distinct complex numbers z1andz2 both satisfy the equation z+¯z=2|z−1|andarg(z1−z2)=π4, then
Az1andz2 lie on a parabolaBRe (z1+z2)=2Clm (z1+z2)=2Dno such z1andz2 exist - Question 3 - Select One
Consider the complex numbers z1 and z2 Satisfying the relation |z1+z2|2=|z1|+|z2|2
Complex number z1/z2 isApurely realBpurely imaginaryCzeroDnone of these
If z1andz2 both satisfy the relation z+¯z=2|z−1|andarg(z1−z2)=π4, then Im(z1+z2) equals
View SolutionFor any two complex numbers z1 and z2, prove that |z1+z2|≤|z1|+|z2|, |z1−z2|≤|z1|+|z2|, |z+1+z2|≥|z1|−|z2| and |z1−z2|≥|z1|−|z2|
View SolutionIf |z1|=1,|z2|=1 then prove that |z1+z2|2+|z1−z2|2 =4.
View SolutionConsider the complex numbers z1 and z2 Satisfying the relation |z1+z2|2=|z1|+|z2|2 Complex number z1¯z2 is
View SolutionIf z1,z2,z3 are vertices of a triangle such that |z1−z2|=|z1−z3|, then arg (2z1−z2−z3z3−z2) is :
View Solution
