If $| z - 1 | = 1$ and arg $(z) = θ$ , where $z \neq 0$ and $θ$ is acute, then $(1 - \frac{2}{z})$ is equal to

A

$tan θ$

B

$I tan θ$

C

$\frac{tan θ}{2}$

D

$I \frac{tan θ}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

We have,
$| z - 1 | = 1$
$\Rightarrow | z - 1 (1 + 0 i) | = 1$
$\Rightarrow$ z lies on the circle with center at (1,0) and radius 1.

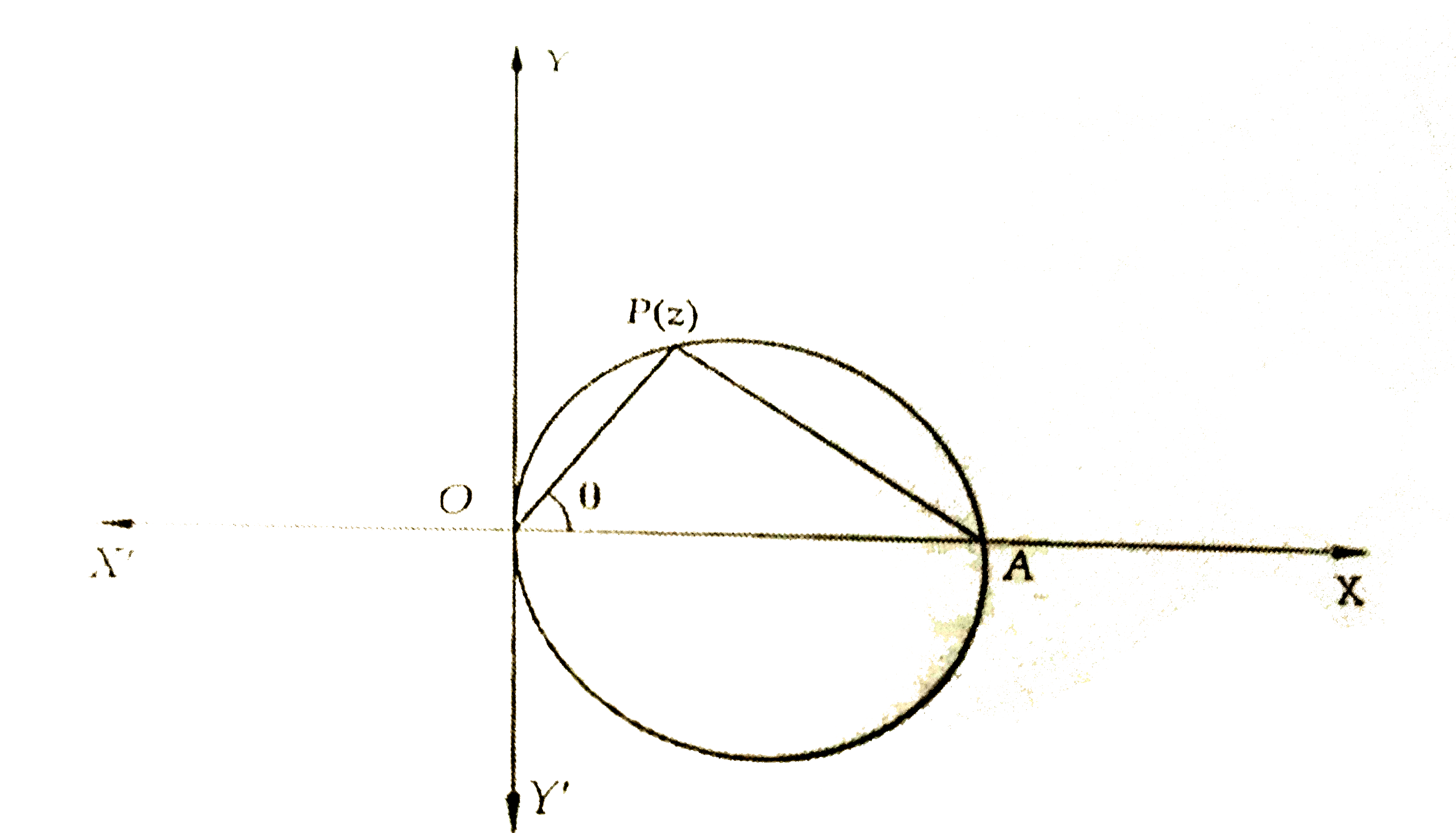
It is given that $θ$ is acute and P(z) is a point on the circle $| z - 1 | = 1$ such that arg (z) $= θ$ , i.e. $∠ A O P = θ$
Now, $a n l \geq O P A = \frac{π}{2}$
$\Rightarrow (2 - z) = \frac{P A}{P O} (0 - z) e^{i π / 2}$
$\Rightarrow \frac{z - 2}{z} = i tan θ [∴ tan θ = \frac{P A}{P} O)]$
$\Rightarrow \frac{z - 2}{z} = i tan θ$

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $| z - i | = 1$ and arg (z) $= θ$ where $0 < θ < \frac{π}{2}$ , then $cot θ - \frac{2}{z}$ equals
A $2 i$
B $- i$
C $i$
D $1 + i$
Question 2 - Select One
If $| z - 1 | = 1,$ then arg (z) is equal to
A $\frac{1}{2} a r g (z)$
B $\frac{1}{3} a r g (z + 1)$
C $\frac{1}{2} a r g (z - 1)$
DNone of these
Question 3 - Select One
If $a r g (z) = θ$ , arg( $¯ z$ ) is equal to
A $θ - π$
B $π - θ$
C $θ$
D $- θ$

OBJECTIVE RD SHARMA-COMPLEX NUMBERS -Section I - Solved Mcqs

Home
Ask Doubt
Profile