The stopping potential as a function of the frequency of the incident radiation is plotted for two different photoelectric surfaces A and B . The graphs show that work function of A is

greater than that of B
smaller than that of B
same as that of B
such that no comparison can be done from given graphs
The correct Answer is:B
Step by step video, text & image solution for The stopping potential as a function of the frequency of the incident radiation is plotted for two different photoelectric surfaces A and B . The graphs show that work function of A is by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MISCELLANEOUS (TOPICS OF GENERAL INTEREST)BOOK - OP TANDONCHAPTER - MISCELLANEOUS (TOPICS OF GENERAL INTEREST)EXERCISE - SET-V: Matching type Questions
37 Videos
- INTRODUCTION TO ORGANIC CHEMISTRY BOOK - OP TANDONCHAPTER - INTRODUCTION TO ORGANIC CHEMISTRY EXERCISE - SINGLE INTEGER ANSWER TYPE
4 Videos
- OXIDATION AND REDUCTION (REDOX REACTIONS)BOOK - OP TANDONCHAPTER - OXIDATION AND REDUCTION (REDOX REACTIONS)EXERCISE - SECTION V
3 Videos
Similar Questions
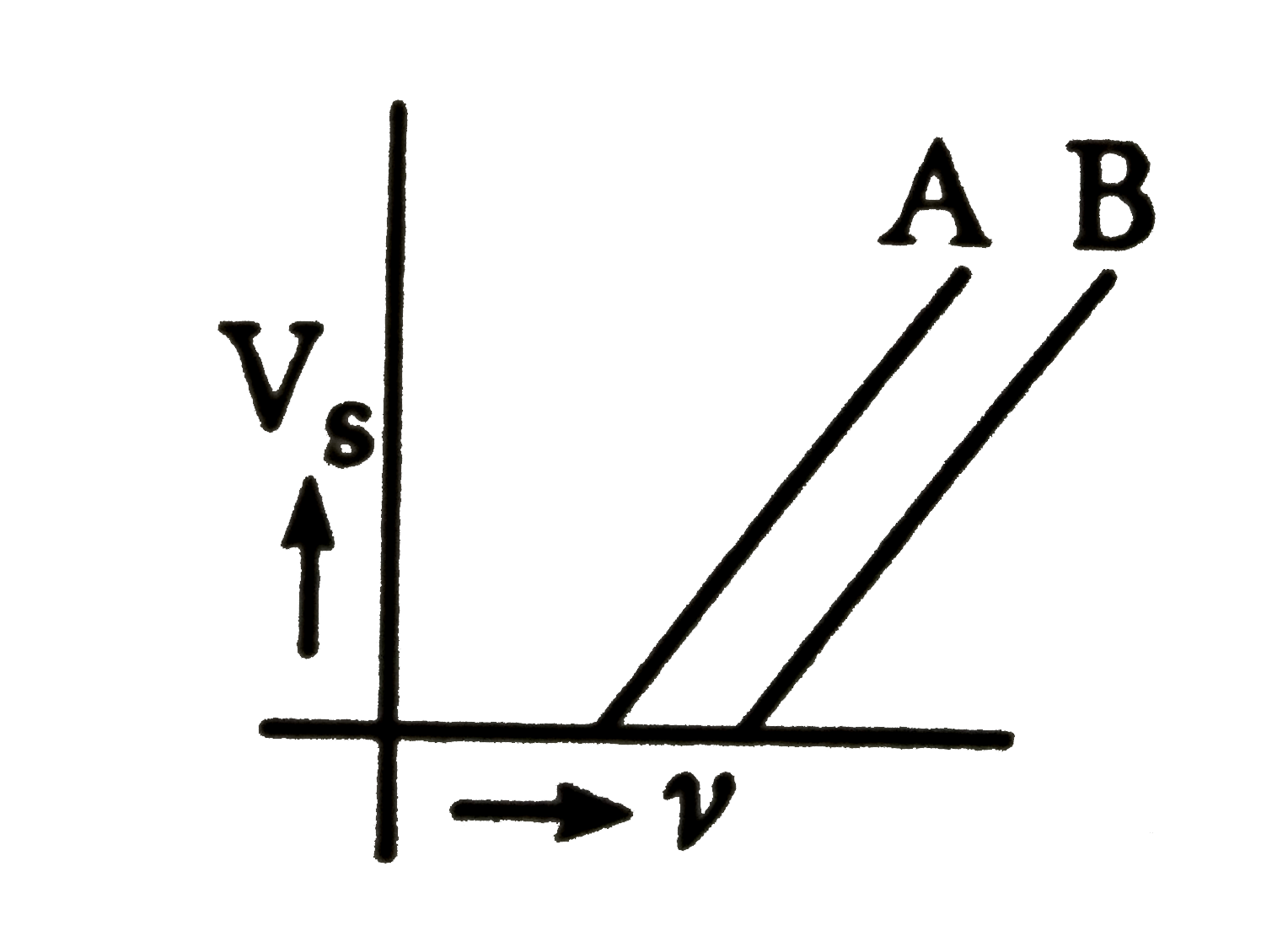
The stopping potential as a function of frequency of incident radiation is plotted for two different photoelectric surfaces A and B . The graphs as shown in figure shows that , the work function of A is
View SolutionThe following figure shows a graph for the stopping potential as a function of the frequency of incident light illuminating a metal surface. Find the photoelectric work function for this surface.
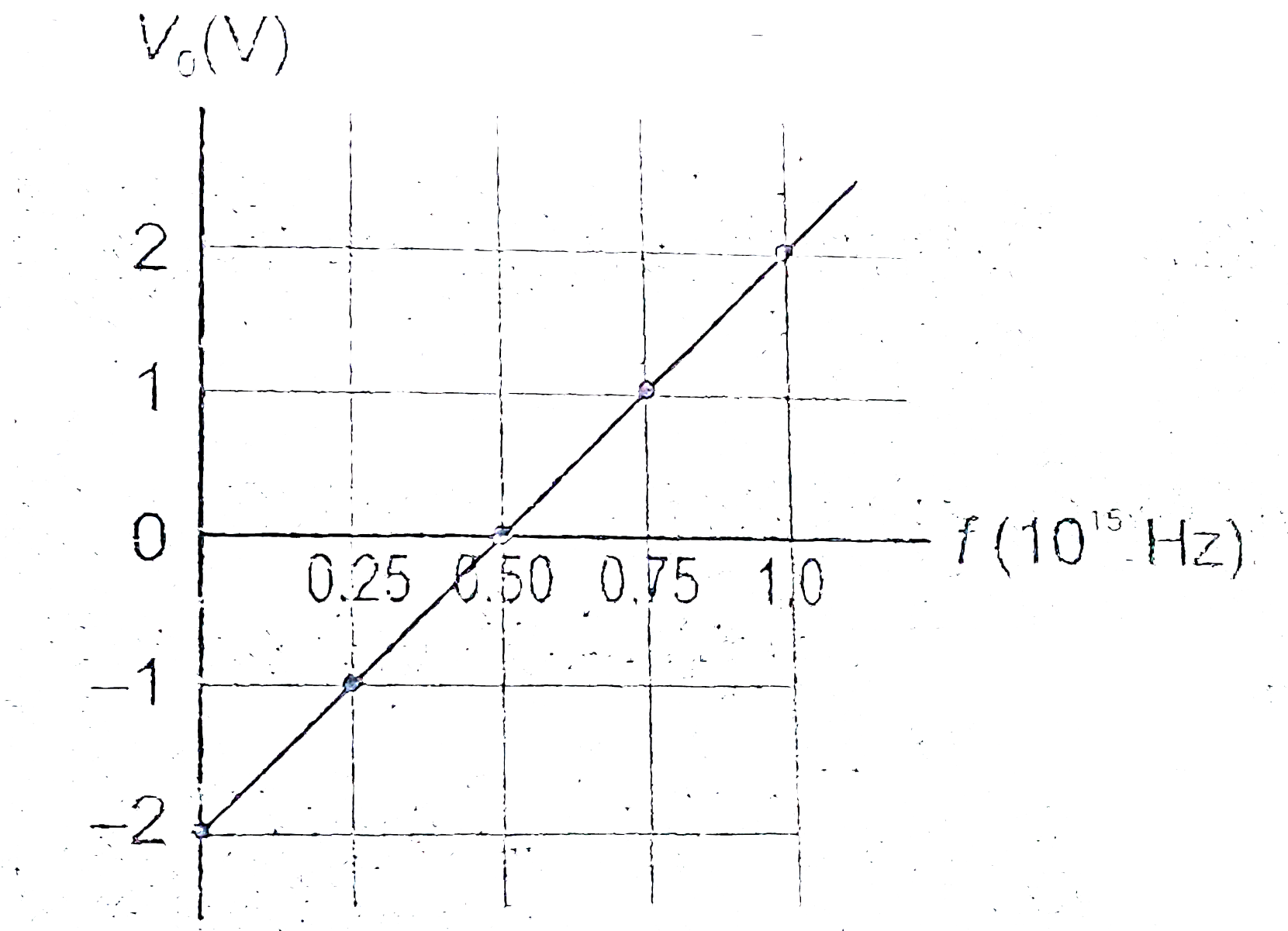
View Solution
Knowledge Check
The stopping potential as a function of the frequency of the incident radiation is plotted for two different photoelectric surfaces A and B . The graphs show that work function of A is
 AGreater than that of BBSmaller than that of BCSame as that of BDNo comparison can be done from given graphs
AGreater than that of BBSmaller than that of BCSame as that of BDNo comparison can be done from given graphsThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectroic effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejercted electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Aborbed energy - Work function
12mv2max=h(v)−h(vn)=hv[1λ−01λn]
Where vn and λ0 are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if V0 is the stopping potential eV0=h(v−v0)
The stopping potential as a function on electron frtequency is plotted for two photoelectric surface A abd B The graph show that the work function of A is
 AGreater than that of BBSmaller than that of BCSame as that of BDSuch that no comparison can be done from given graph
AGreater than that of BBSmaller than that of BCSame as that of BDSuch that no comparison can be done from given graphFigure show the variation of the stopping potential (V0) with the frequency (v) of the incident radiations for two different photosensitive matererial M1 and M2 What are the values of work functions for M1 and M2 respectively
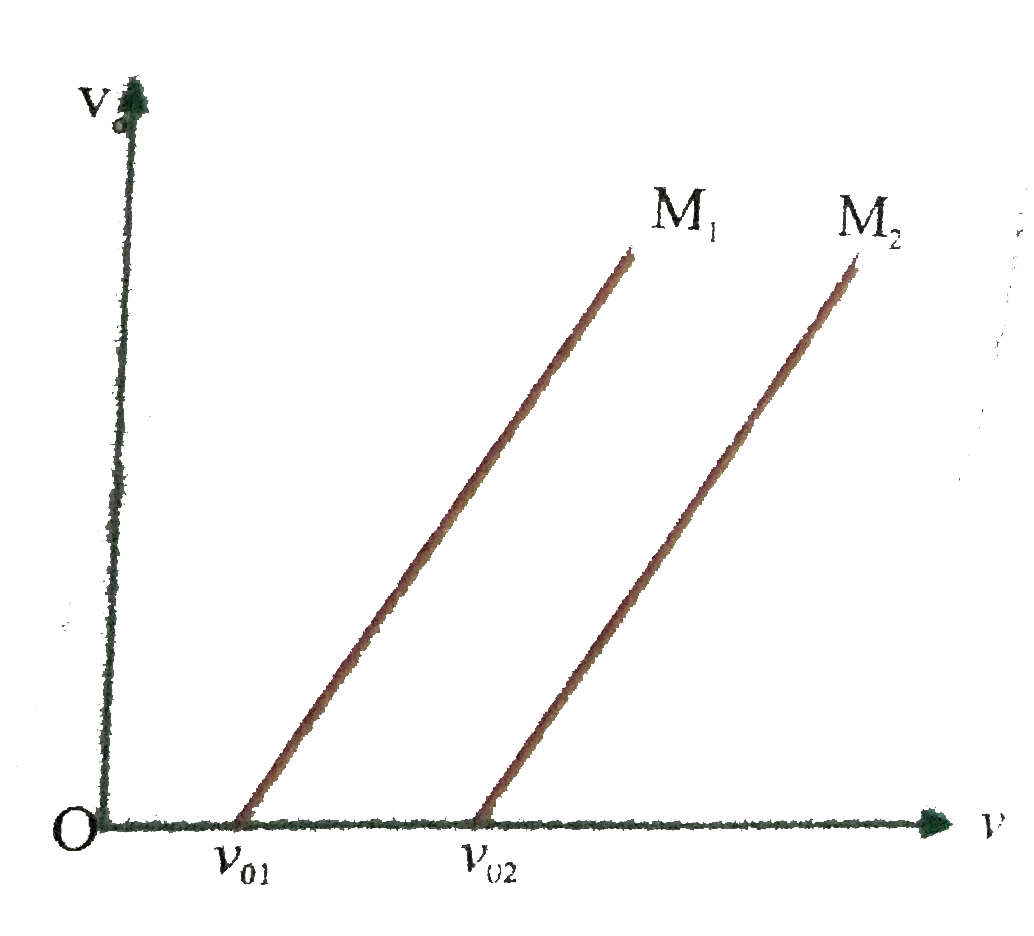 Ahv01,hv02Bhv02,hv01Chv01,hv01Dhv02,hv02
Ahv01,hv02Bhv02,hv01Chv01,hv01Dhv02,hv02
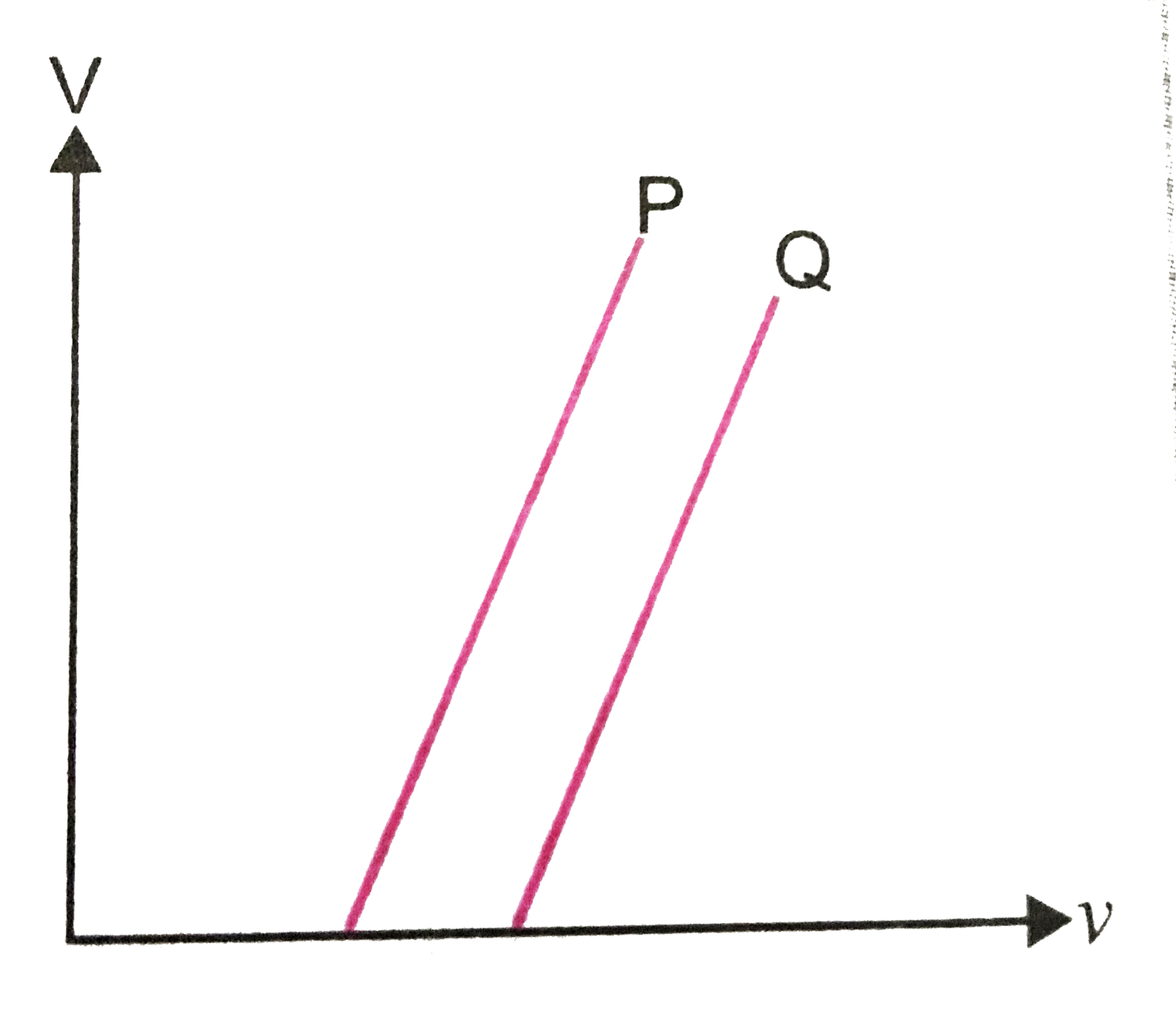
In a photoelectric effect experiment, the graph between the stopping potential (V) and frequency (v) of the incident radiations on two different metal plates P and Q are shown in plates, P and Q has greater value of work function ? (ii) What does the slope of the lines depict?
View SolutionAt frequencies of the incident radiation above the threshold frequency, the photoelectric current in a photoelectric
View SolutionWhat is the effect of decrease in frequency of incident radiation on the stopping potential in photoelectric emission?
View SolutionThe stopping potential (v0) varies linearly with the frequency (v)of the incident radiation for a given photosensitive surface with the slope remaining the same for different surface . Given reason.
View SolutionThe variation of the stopping potential (V0) with the frequency (v) of the light incident on two different photosensitive surfaces M1andM2 is shown in the figure. Identify the surfaces which has greater value of the work function.

View Solution
