van der Waal's gas equation can be reduced to virial eqation and virial equation (in terms of volume) isZ=A+BVm+CV2m+……..
where A =first virial coefficient, B=second virial coefficient ,C = third virial coefficient. The third virial coeffdient of Hg(g) is 625 (cm2/mol)2. What volume is available for movement of 10 moles He(g) atoms present in 50 L vessel?
49.75 L
49.25 L
25 L
50 L
The correct Answer is:a
To solve the problem, we need to determine the volume available for the movement of 10 moles of helium gas in a 50 L vessel, taking into account the third virial coefficient of mercury.
1. Identify the Given Data:
- Third virial coefficient (C) for Hg(g) = 625 cm³/mol².
- Number of moles of He (n) = 10 moles.
- Total volume of the vessel (V) = 50 L.
2. Convert Units:
- Since the third virial coefficient is given in cm³/mol², we need to convert the volume of the vessel from liters to cm³:
50L=50×1000cm3=50000cm3
3. Calculate the Second Virial Coefficient (B):
- The third virial coefficient (C) is related to the second virial coefficient (B) as follows:
C=B2
- Therefore, we can find B:
B=√C=√625cm3/mol2=25cm3/mol
4. Calculate the Real Volume Available (V_real):
- The real volume available for the gas can be calculated using the formula:
Vreal=Videal−nB
- Substituting the values:
Vreal=50000cm3−(10mol×25cm3/mol)
Vreal=50000cm3−250cm3=49750cm3
5. Convert Real Volume Back to Liters:
- Convert the real volume from cm³ back to liters:
Vreal=49750cm31000=49.75L
Final Answer:
The volume available for the movement of 10 moles of He(g) atoms present in a 50 L vessel is 49.75 L.
- Third virial coefficient (C) for Hg(g) = 625 cm³/mol².
- Number of moles of He (n) = 10 moles.
- Total volume of the vessel (V) = 50 L.
- Since the third virial coefficient is given in cm³/mol², we need to convert the volume of the vessel from liters to cm³:
50L=50×1000cm3=50000cm3
- The third virial coefficient (C) is related to the second virial coefficient (B) as follows:
C=B2
- Therefore, we can find B:
B=√C=√625cm3/mol2=25cm3/mol
- The real volume available for the gas can be calculated using the formula:
Vreal=Videal−nB
- Substituting the values:
Vreal=50000cm3−(10mol×25cm3/mol)
Vreal=50000cm3−250cm3=49750cm3
- Convert the real volume from cm³ back to liters:
Vreal=49750cm31000=49.75L
The volume available for the movement of 10 moles of He(g) atoms present in a 50 L vessel is 49.75 L.
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 14videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 26videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Subjective problems15videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems14videos
ELECTROCHEMISTRY
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems1videos
IONIC EEQUILIBRIUM
Similar Questions
Virial equation is: PVM=RT[A+BVM+CVM2+…], where A, B, C, …. are first second,third, … virial coefficent, respectively, For an ideal gas
View SolutionThe virial equation for 1mole of a real gas is written as :
PV=RT
[1+AV+BV2+CV3+ ........ To higher power of n]
Where A,B, and C are known as virial coefficients . If Vander wall's equation is written in virial form, then what will be value of B:View SolutionThe van der Waals' equation for one mole may be expressed as
V3M−(b+RTP)V2m+aVmP−abP=0
where Vm is the molar volume of the gas. Which of the followning is incorrect?View SolutionAt low pressure, the van der Waal's equation become :
(a)PVm=RT
(b)P(Vm−b)=RT
(c)(P+aV2M)Vm=RT
(d)P=RTVm+aV2mView SolutionThe van der Waal's equation of state for some gases can be expressed as :
(P+aV2)(V−b)=RT
Where P is the pressure , V is the molar volume , and T is the absolute temperature of the given sample of gas and a,b,andR are constants.
The dimensions of a areView SolutionThe Van der waal's equation for n moles of a real gas is given by (P+n2aV2)(V−nb)=nRT, where
P pressure of gas, V= volume of gas, T= temperature of gas
R= molar gas constant, a & b= Van der waal's constant
Which of the following have the same dimensions as those of nRT.View SolutionUsing van der Waals equation (P+aV2)(V−b)=RT, answer the following questions:
The term that accounts for effective volume in the van der Waals equation for non-ideal gas isView SolutionThe van der wasl's equation of a gas is (P+aT2V)Vc=(RT+b). Where a, b, c and R are constant. If the isotherm is represented by P=AVm−BVn, where A and B depends on temperature:
View Solutionvan der Waal's equation for calculating the pressure of a non ideal gas is
(P+an2V2)(V−nb)=nRT
van der Waal's suggested that the pressure exerted by an ideal gas , Pideal, is related to the experiventally measured pressure, Pideal by the equation
Pideal=Preal↑observed pressure+an2V2↑currection term
Constant 'a' is measure of intermolecular interaction between gaseous molecules that gives rise to nonideal behavior. It depends upon how frequently any two molecules approach each other closely. Another correction concerns the volume occupied by the gas molecules. In the ideal gas equation, V represents the volume of the container. However, each molecule does occupy a finite, although small, intrinsic volume, so the effective volume of the gas vecomes (V-nb), where n is the number of moles of the gas and b is a constant. The term nb represents the volume occupied by gas particles present in n moles of the gas .
Having taken into account the corrections for pressure and volume, we can rewrite the ideal gas equation as follows :
(P+an2V2)corrected pressure(V−nb)corrected volume=nRT
AT relatively high pressures, the van der Waals' equation of state reduces toView SolutionAt a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
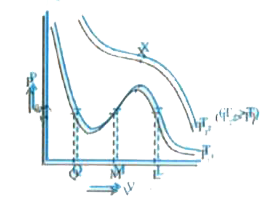
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given asView Solution
