A 3kg block of wood is on a level surface where μs=0.25 and μs=0.2A force of 7N is being applied horizontal to the block Mark the correct statement(s) regarding this situation.
If the block is initially at rest , it will remain at rest and friction force will be about ?7N
If the block is initially moving than it will continue its motion forever if the force applies is in the direction of the motion of the block
If the block is initially moving and the direction of applied force is mass as that of motion of block , than block moves with an acceleration of 1/3ms−2 along its initial direction of motion
If the block is initially moving and direction of applied force to that of initial motion of the blockthan the block decelerates comes to a stop and starts moving in the opposite direction.
The correct Answer is:a,b,c
To solve the problem, we need to analyze the situation involving a 3 kg block of wood on a level surface with given coefficients of static and kinetic friction. We will determine the correct statements regarding the block's motion under the influence of an applied force of 7 N.
1. Identify the Forces Acting on the Block:
- The weight of the block (W) can be calculated using the formula:
W=m⋅g
where m=3kg and g=9.8m/s2.
W=3kg×9.8m/s2=29.4N
- The normal force (N) acting on the block is equal to its weight since the surface is level:
N=W=29.4N
2. Calculate Maximum Static Friction (F_s_max):
- The maximum static friction can be calculated using the coefficient of static friction (μs=0.25):
Fsmax=μs⋅N=0.25×29.4N=7.35N
3. Calculate Kinetic Friction (F_k):
- The kinetic friction can be calculated using the coefficient of kinetic friction (μk=0.2):
Fk=μk⋅N=0.2×29.4N=5.88N
4. Analyze the Applied Force:
- An applied force of 7 N is acting on the block. Since 7N<7.35N, the block will remain at rest because the applied force does not exceed the maximum static friction.
5. Evaluate the Statements:
- Statement A: If the block is initially at rest, it will remain at rest. This statement is true because the applied force (7 N) is less than the maximum static friction (7.35 N).
- Statement B: If the block is initially moving, it will continue its motion forever if the force applied is in the direction of motion. This statement is true because once in motion, the applied force (7 N) exceeds the kinetic friction (5.88 N), allowing continuous motion.
- Statement C: If the block is initially moving in the direction of the applied force, it will move with an acceleration of 13m/s2. This statement is true because the net force when moving is 7N−5.88N=1.12N, leading to an acceleration of:
a=Fnetm=1.12N3kg≈0.373m/s2
- Statement D: If the block is initially moving in the direction of the applied force, it will decelerate and stop, then move in the opposite direction. This statement is false because the block will not reverse direction unless the applied force is less than the opposing friction force.
Conclusion:
The correct statements are A, B, and C.
- The weight of the block (W) can be calculated using the formula:
W=m⋅g
where m=3kg and g=9.8m/s2.
W=3kg×9.8m/s2=29.4N
- The normal force (N) acting on the block is equal to its weight since the surface is level:
N=W=29.4N
- The maximum static friction can be calculated using the coefficient of static friction (μs=0.25):
Fsmax=μs⋅N=0.25×29.4N=7.35N
- The kinetic friction can be calculated using the coefficient of kinetic friction (μk=0.2):
Fk=μk⋅N=0.2×29.4N=5.88N
- An applied force of 7 N is acting on the block. Since 7N<7.35N, the block will remain at rest because the applied force does not exceed the maximum static friction.
- Statement A: If the block is initially at rest, it will remain at rest. This statement is true because the applied force (7 N) is less than the maximum static friction (7.35 N).
- Statement B: If the block is initially moving, it will continue its motion forever if the force applied is in the direction of motion. This statement is true because once in motion, the applied force (7 N) exceeds the kinetic friction (5.88 N), allowing continuous motion.
- Statement C: If the block is initially moving in the direction of the applied force, it will move with an acceleration of 13m/s2. This statement is true because the net force when moving is 7N−5.88N=1.12N, leading to an acceleration of:
a=Fnetm=1.12N3kg≈0.373m/s2
- Statement D: If the block is initially moving in the direction of the applied force, it will decelerate and stop, then move in the opposite direction. This statement is false because the block will not reverse direction unless the applied force is less than the opposing friction force.
The correct statements are A, B, and C.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A block of mass √3kg is kept on a frictional surface with μ=12√3. The minimum force to be applied as shown to move the block is

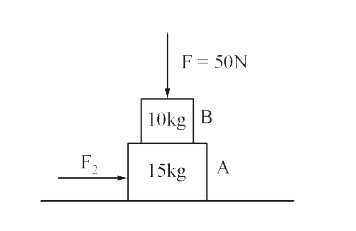
View SolutionBlock B is kept on Block A and a force F = 50 N pushes B down as shown in figure. Block A is kept on a rough surface with μs=0.2 and μk=0.1 . What is the maximum force F2 which can be applied so that the system remains at rest?
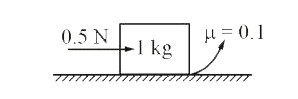
View SolutionA block of mass 1 kg in kept on a rough horizontal surface with μs=0.1 . A force of 0.5 N is applied as shown in the figure. What is the frictional force applied by ground on the block?
View SolutionA block of mass 5 kg is kept on a rough horizontal surface. The coefficient of friction for the contact force block and surface are μs=0⋅1andμk=0⋅9 respectively . A horizontal force F given by F 0⋅5t is applied at t = 0 . Here t represent time in seconds . Determine the force of friction and acceleration of the block at
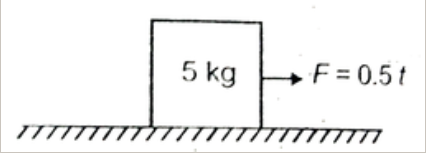
(i) t = 1s (ii) t= 10 s (iii) t = 12 s
View SolutionIn Fig the block are at rest a force of 10N act on the block of 4kg mass .The coefficient of staic friction and the coefficient of kinetic friction are μs=0.2andμs=0.15 for both the surface in contact The magnitudeof frcition force acting between the surface of contact between the 2kg and 4kg block in this situation is

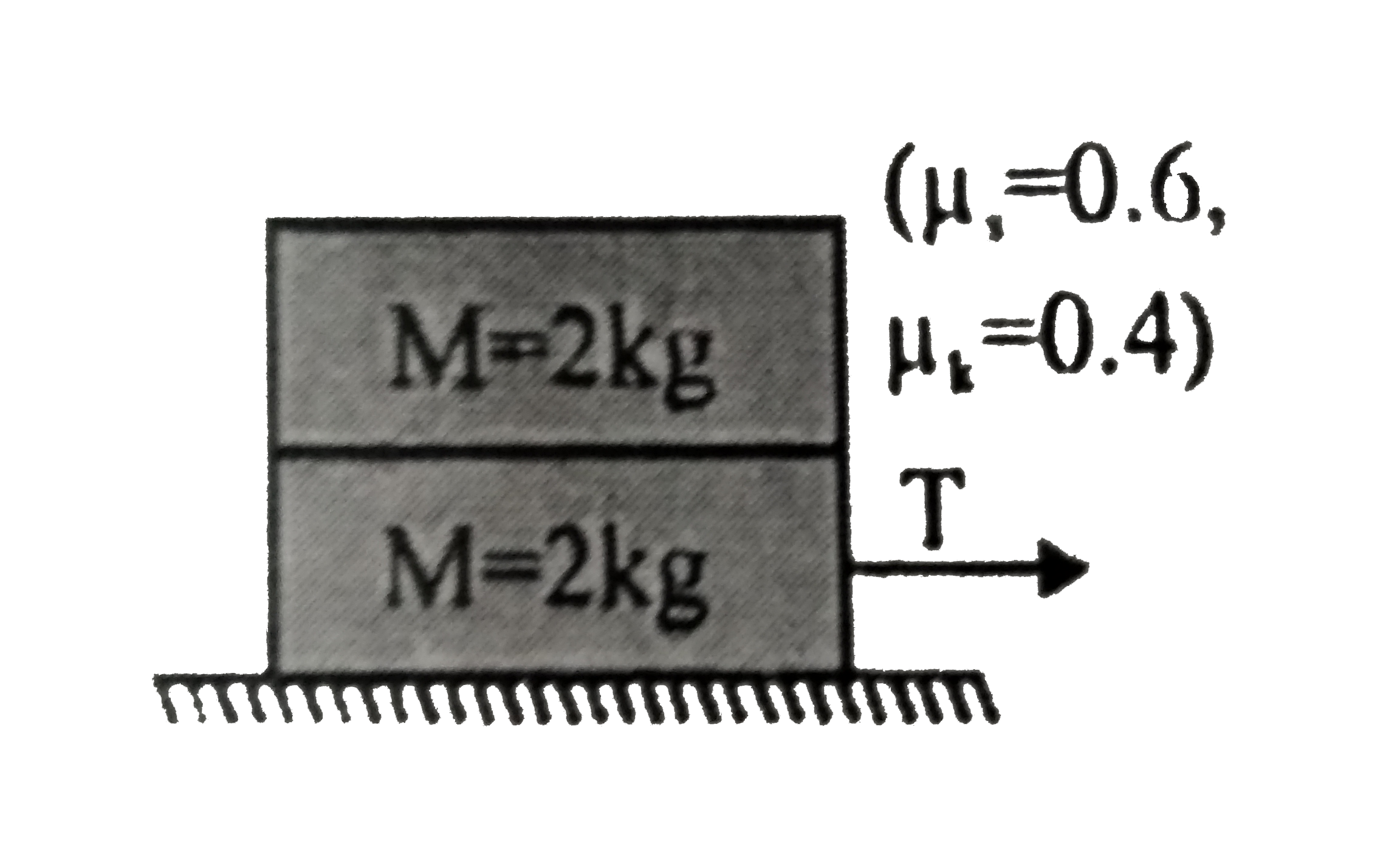
View SolutionThe coefficient of static and kinetic friction between the two blocks and also between the lower block and the ground are μs=0.6andμk=0.4 Find the value of tension T applied on the lower block at which the upper block begins to slip relative to lower block.
View SolutionA block of mass 1 kg is placed on a surface for which μs=0.2&μk=0.15, an external force F is applied on the block as shown in the figure, using g=10m/sec2, find:
(a) The force of friction on block
(b) Its acceleration
(i) When F=1 N
(ii) When F=2 N
(iii) When F=2.5 N

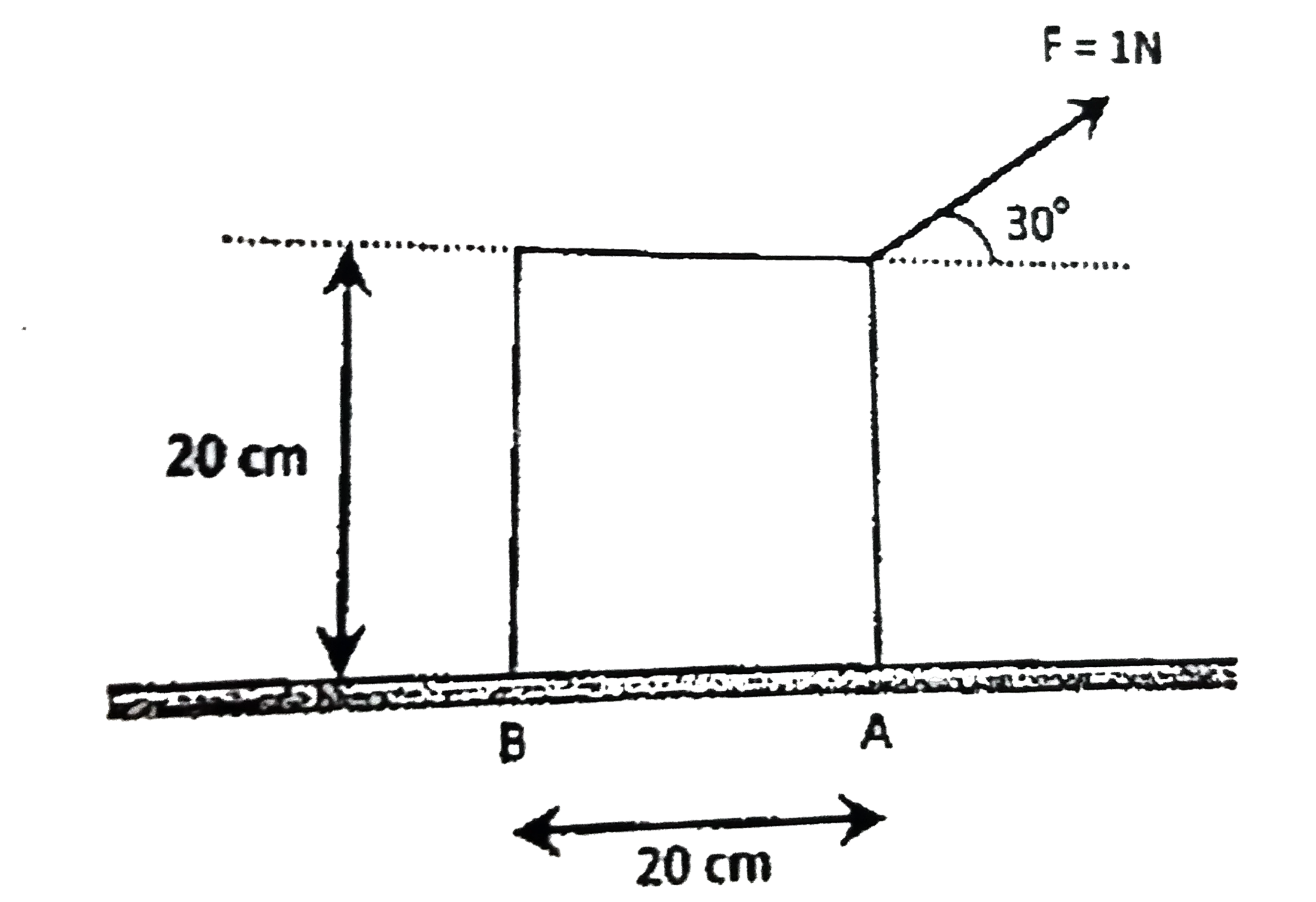
View SolutionA block of mass √3/10kg is placed on a rough horizontal surface as shown in the figure. A force of 1N is applied at one end of the block and the block remains stationary. The normal force exerted by the sruface on the block acts(g=10m/s2)
View SolutionA block of mass 2 kg rests on a horizontal surface. If a horizontal force of 5 N is applied on the block, the frictional force on it is (take,uk=0.4,μs=0.5)
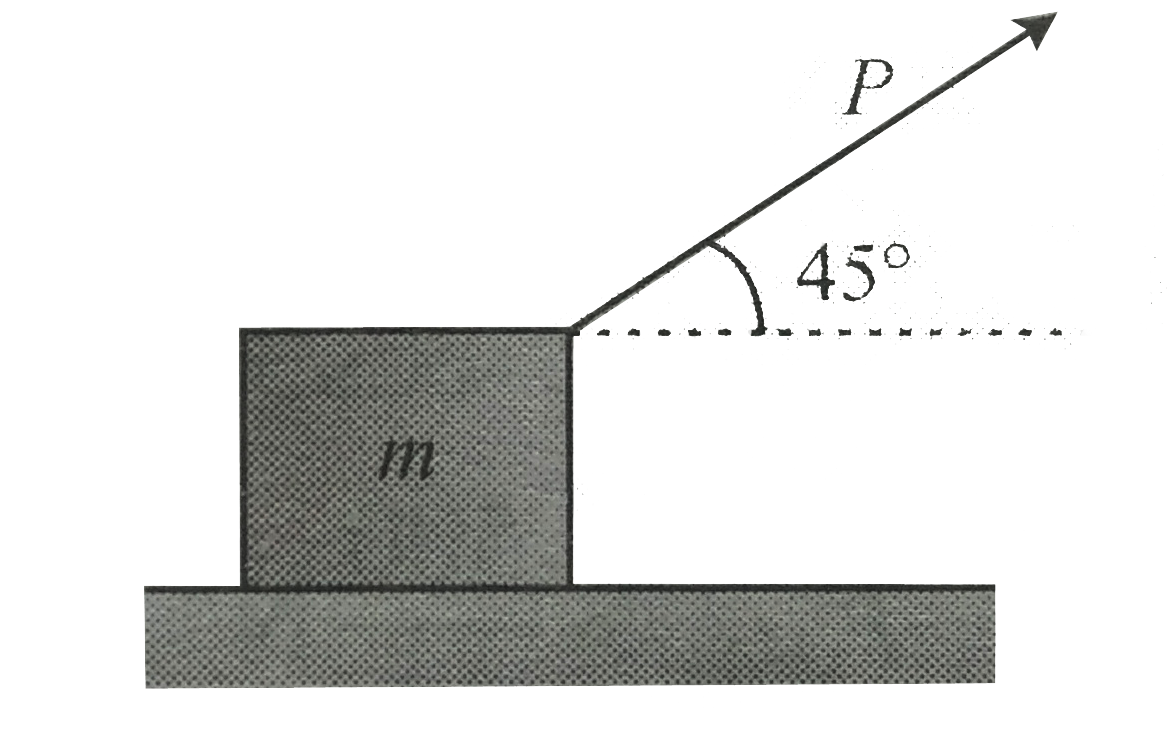
View SolutionFind the least pulling force which acting at an angle of 45∘ with the horizontal will slide a body weighing 5kg along a rough horizontal surface . The coefficient of friction μs=μk=1/3 If a force of doude this is applied along the same direction , find the resulting acceleration of the block
View Solution
