A battery with negligible internal resistance, a resistor, and a inductor with negligible resistance are all connected in series with an open switch. The switch is suddenly closed
(a) How long after closing the switch will the current through the inductor reach one-half of its maximum value?
(b) How long after closing the switch will the energy stored in the inductor reach one-half of its maximum value?
The correct Answer is:C
To solve the problem step by step, we will address both parts (a) and (b) separately.
Part (a): Time for Current to Reach One-Half of Its Maximum Value
1. Identify the Maximum Current (I₀):
The maximum current in the circuit can be calculated using Ohm's Law:
I0=VR
where V=35.0V and R=50.0Ω.
I0=35.050.0=0.7A
2. Determine the Time Constant (τ):
The time constant for an RL circuit is given by:
τ=LR
where L=1.25mH=1.25×10−3H and R=50.0Ω.
τ=1.25×10−350.0=2.5×10−5s
3. Find Time for Current to Reach Half of Maximum Value:
The current through the inductor at time t is given by:
I(t)=I0(1−e−tτ)
To find the time when the current reaches half of its maximum value:
I02=I0(1−e−tτ)
Dividing both sides by I0:
12=1−e−tτ
Rearranging gives:
e−tτ=12
Taking the natural logarithm:
−tτ=ln(12)
Thus:
t=−τln(12)=τln(2)
4. Calculate Time:
Substituting the value of τ:
t=(2.5×10−5)ln(2)≈2.5×10−5×0.693≈1.73×10−5s
Part (b): Time for Energy to Reach One-Half of Its Maximum Value
1. Determine Maximum Energy (U₀):
The energy stored in the inductor is given by:
U=12LI2
The maximum energy when the current is at its maximum I0:
U0=12LI20
2. Find Current for Half Maximum Energy:
For the energy to be half of its maximum:
U02=12LI2
This implies:
I=I0√2
3. Use Current Equation:
We know:
I(t)=I0(1−e−tτ)
Setting I(t)=I0√2:
I0√2=I0(1−e−tτ)
Dividing by I0:
1√2=1−e−tτ
Rearranging gives:
e−tτ=1−1√2=√2−1√2
Taking the natural logarithm:
−tτ=ln(√2−1√2)
Thus:
t=−τln(√2−1√2)
4. Calculate Time:
Substituting the value of τ:
t=(2.5×10−5)ln(√2−1√2)
Approximating:
t≈30.7×10−6s
Final Answers:
(a) The time for the current to reach one-half of its maximum value is approximately 1.73×10−5s.
(b) The time for the energy stored in the inductor to reach one-half of its maximum value is approximately 30.7×10−6s.
The maximum current in the circuit can be calculated using Ohm's Law:
I0=VR
where V=35.0V and R=50.0Ω.
I0=35.050.0=0.7A
The time constant for an RL circuit is given by:
τ=LR
where L=1.25mH=1.25×10−3H and R=50.0Ω.
τ=1.25×10−350.0=2.5×10−5s
The current through the inductor at time t is given by:
I(t)=I0(1−e−tτ)
To find the time when the current reaches half of its maximum value:
I02=I0(1−e−tτ)
Dividing both sides by I0:
12=1−e−tτ
Rearranging gives:
e−tτ=12
Taking the natural logarithm:
−tτ=ln(12)
Thus:
t=−τln(12)=τln(2)
Substituting the value of τ:
t=(2.5×10−5)ln(2)≈2.5×10−5×0.693≈1.73×10−5s
The energy stored in the inductor is given by:
U=12LI2
The maximum energy when the current is at its maximum I0:
U0=12LI20
For the energy to be half of its maximum:
U02=12LI2
This implies:
I=I0√2
We know:
I(t)=I0(1−e−tτ)
Setting I(t)=I0√2:
I0√2=I0(1−e−tτ)
Dividing by I0:
1√2=1−e−tτ
Rearranging gives:
e−tτ=1−1√2=√2−1√2
Taking the natural logarithm:
−tτ=ln(√2−1√2)
Thus:
t=−τln(√2−1√2)
Substituting the value of τ:
t=(2.5×10−5)ln(√2−1√2)
Approximating:
t≈30.7×10−6s
(a) The time for the current to reach one-half of its maximum value is approximately 1.73×10−5s.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Single Correct
37 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 More Than One Correct
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions
3 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A simple LR circuit is connected to a battery at time t=0. The energy stored in the inductor reaches half its maximum value at time
View SolutionRefer to Fig. 7.49.
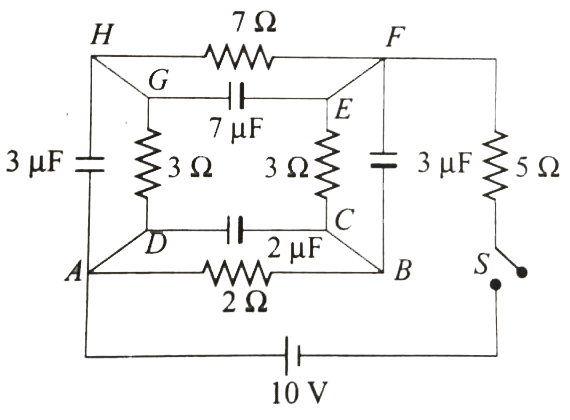
At t=0 , the switch is closed . Just after closing the switch, find the current through the 5Ω resistor.
View SolutionIn the circuit shown in figure the switch S is closed at t = 0. A long time after closing the switch
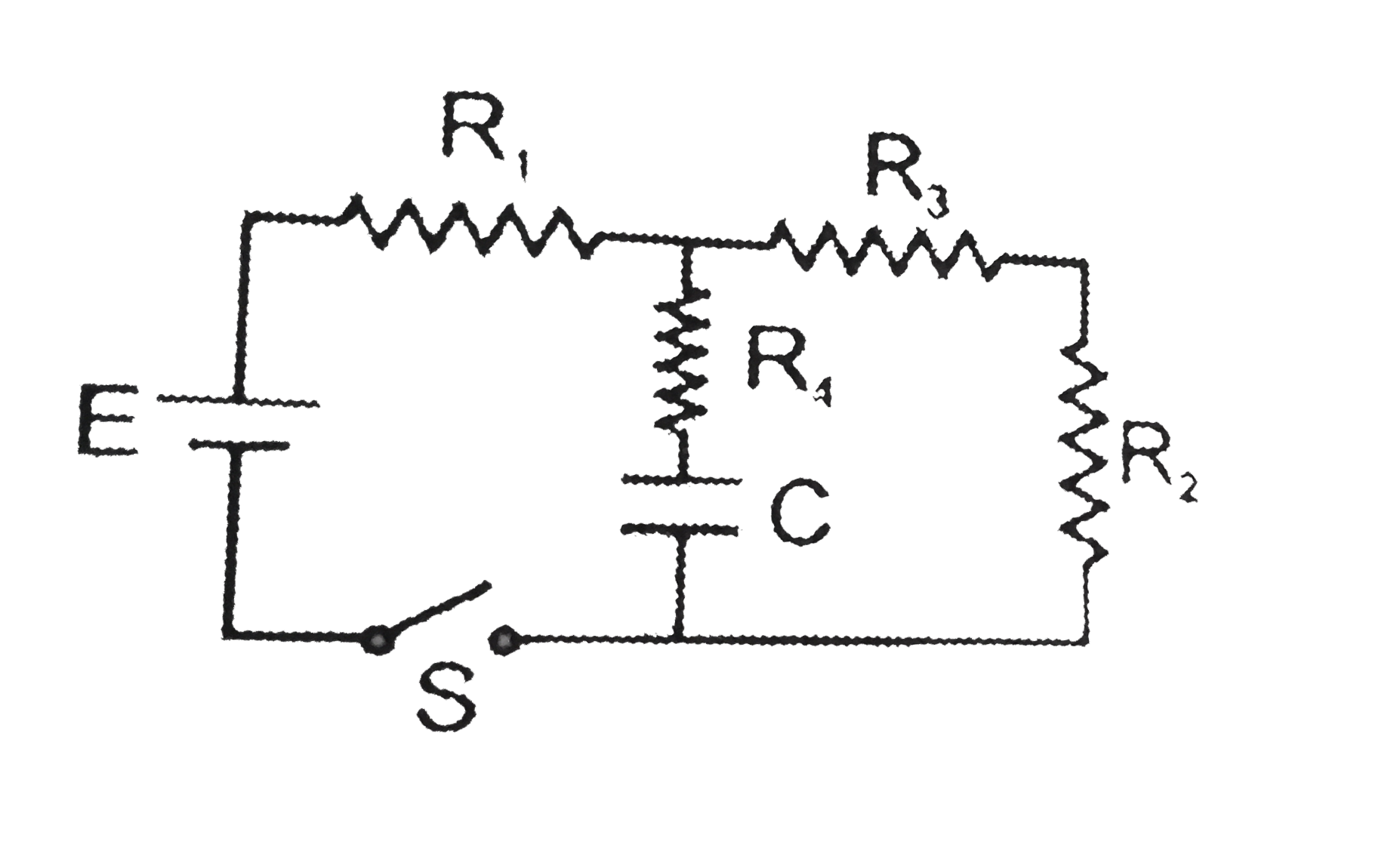
View SolutionRefer to Fig. 7.49.
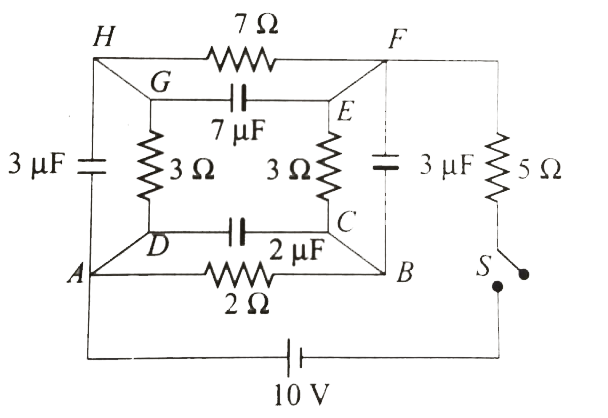
Long time after closing the switch , find the current through the 5Ω resistor.
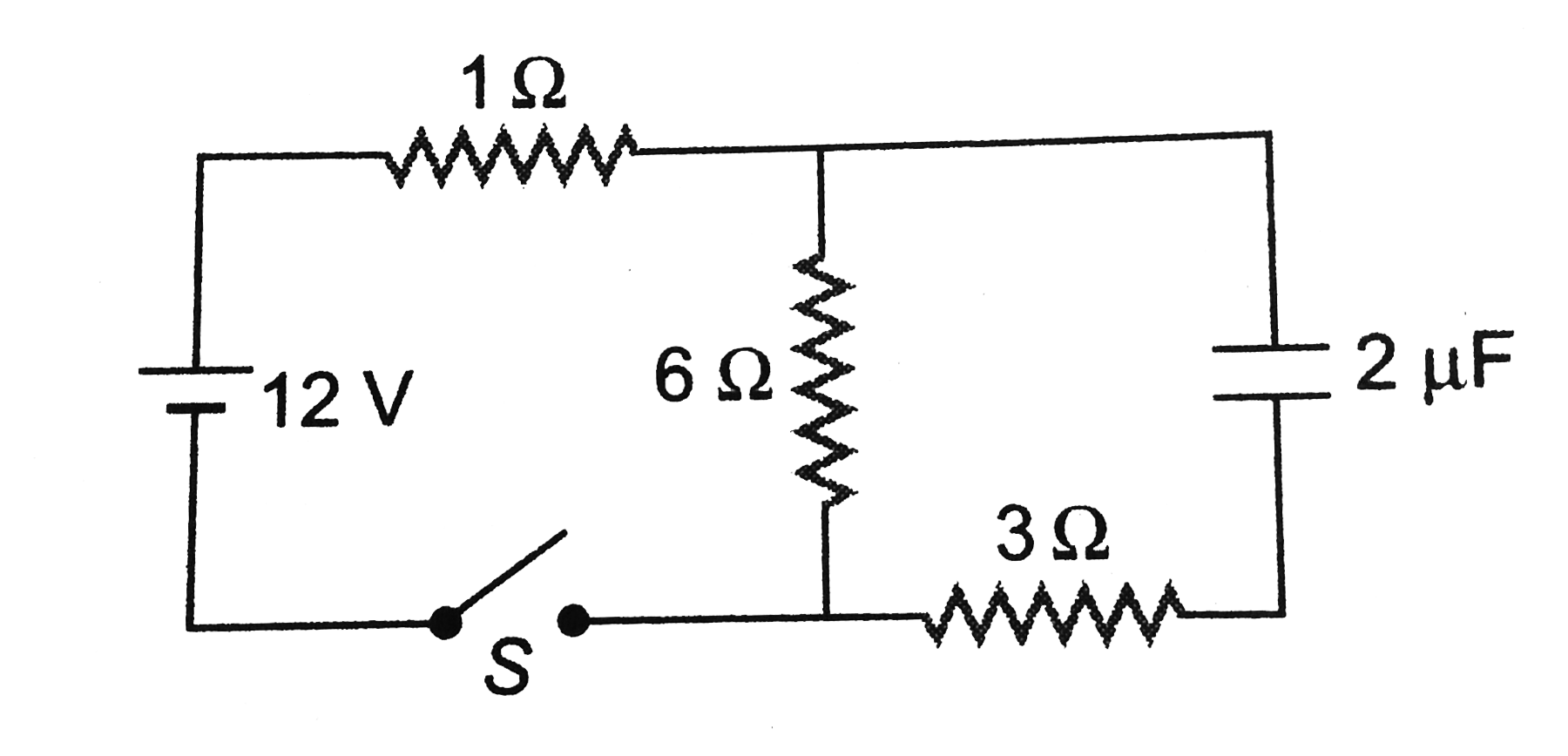
View SolutionWhen the switch is closed, the initial current through the 1Ω resistor is
View SolutionFind current through the battery
(a) just after the switch is closed
(b) long after the switch has been closed
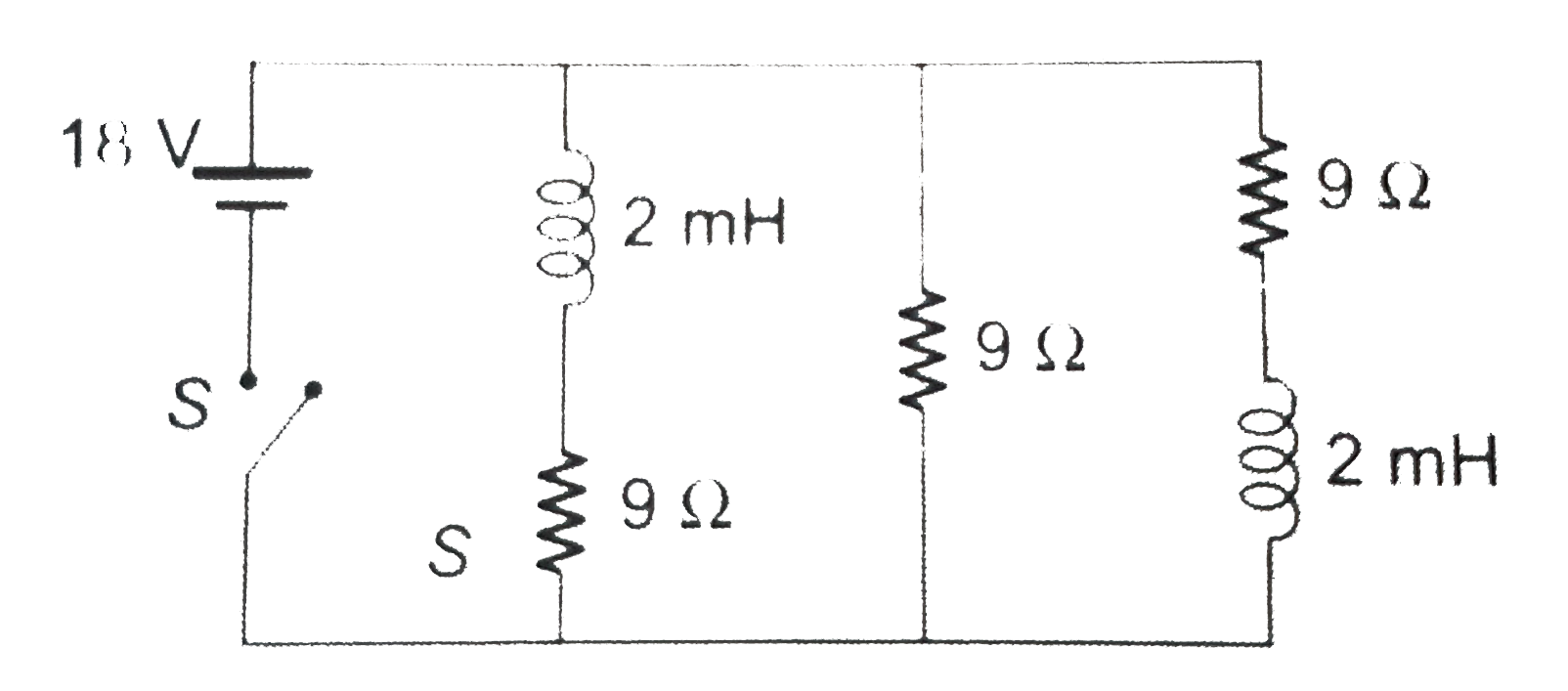
View SolutionAn inductor L and a resistance R are connected in series with a battery of emf E and a switch. Initially the switch is open. The switch is closed at an instant t = 0. Select the correct alternatives
View SolutionFind the current through the battery
(i) just after the switch is closed.
(ii) long after the switch has been closed.
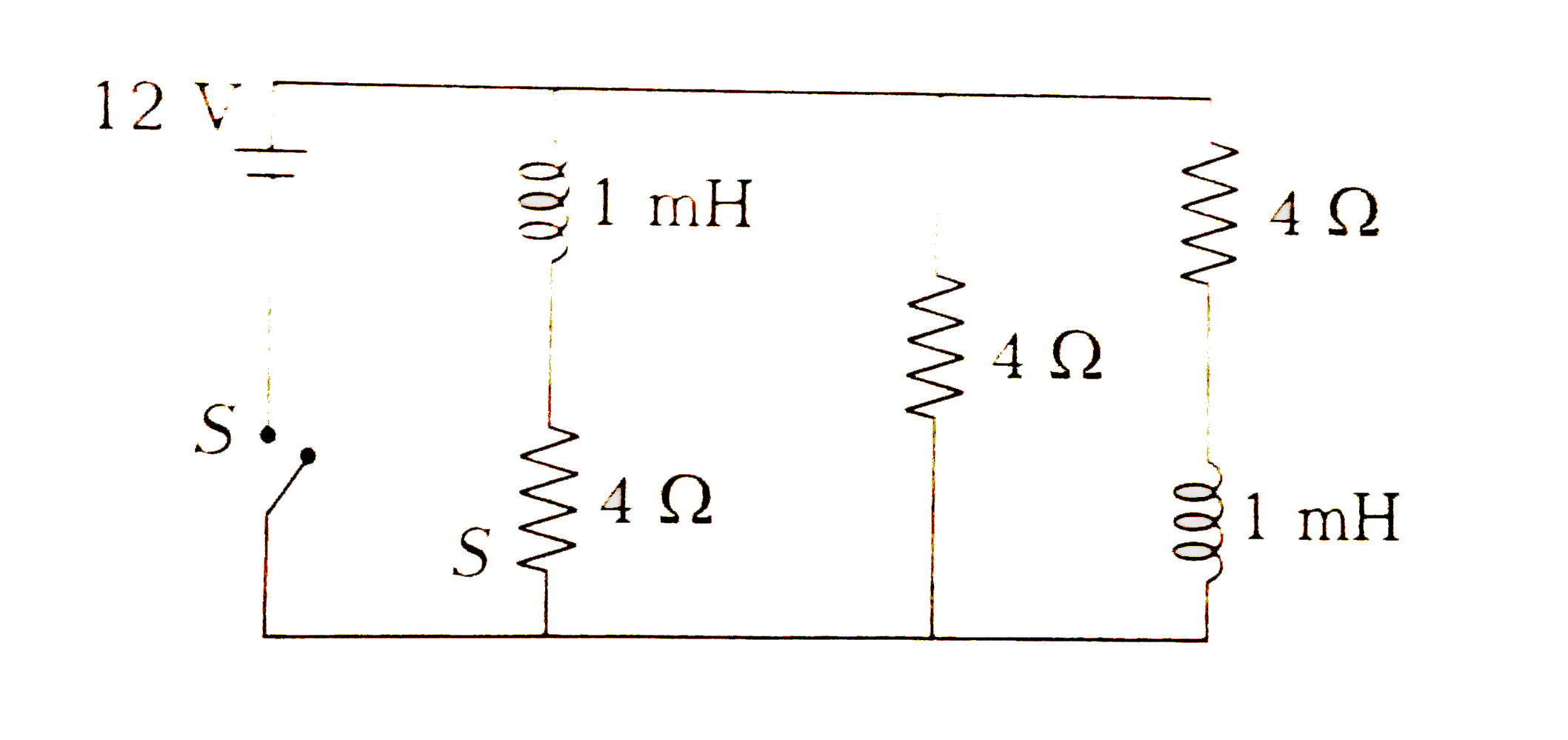
View Solutionshows three resistances are
connected with switch S initially the switch is open. When
the switch S is closed find the current passed through it.
View SolutionAssertion In the figure, just after closing the switch the potential drop across inductor is maximum.
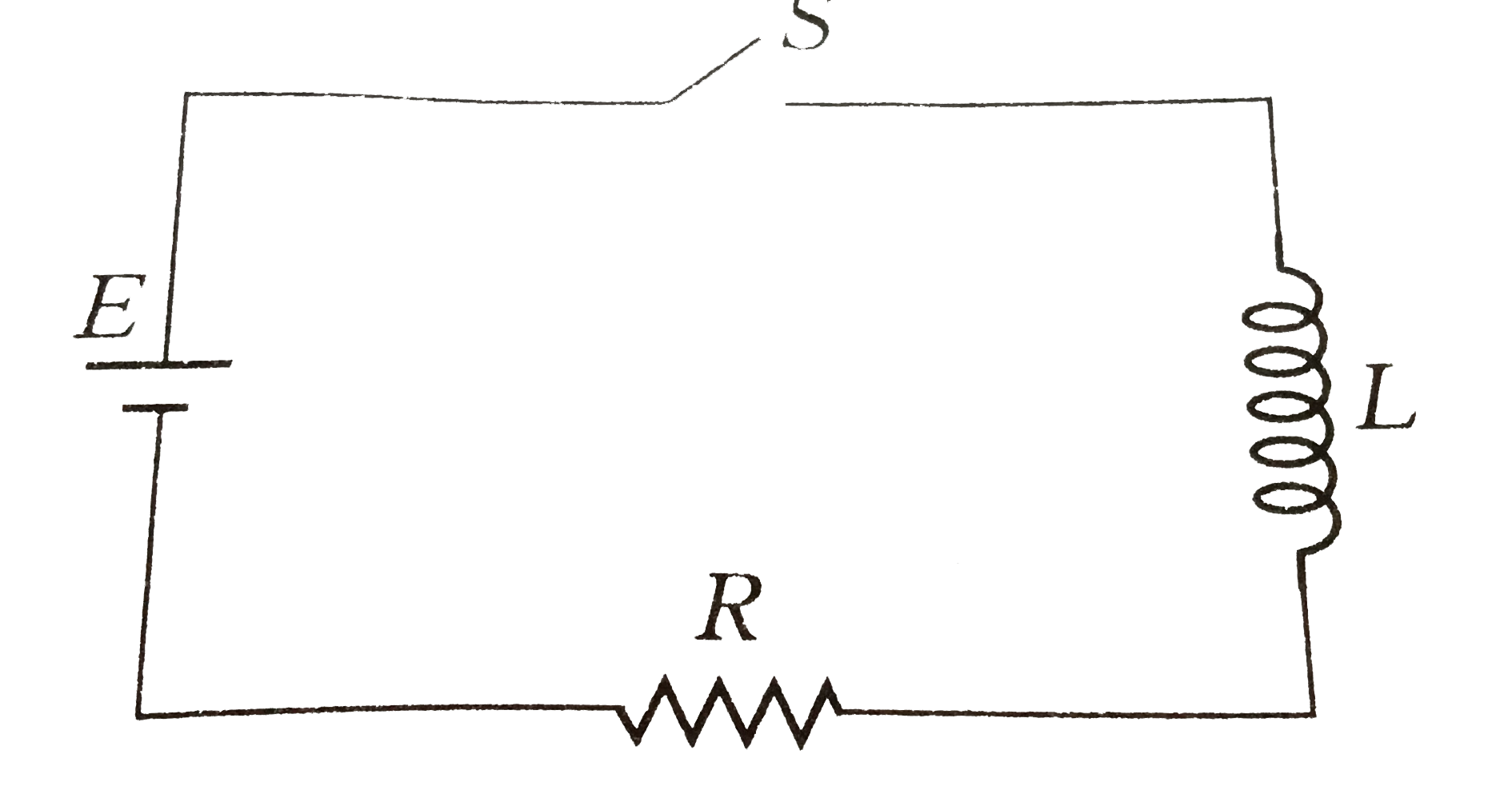
Reason The rate of change of current just after closing the switch is maximum.
View Solution
