A ball strikes a smooth horizontal floor at an angle with the normal to the surface and after rebounding from the floor , ball moves at an angle with the normal . Find the relation between and if coefficient of elasticity is e .
To find the relation between the angles of incidence (α) and reflection (β) of a ball rebounding off a smooth horizontal floor with a coefficient of restitution (e), we can follow these steps:
1. Understanding the Problem:
- A ball strikes the floor at an angle α with the normal (the line perpendicular to the surface).
- After rebounding, it moves at an angle β with the normal.
- The coefficient of restitution (e) relates the velocities before and after the collision.
2. Components of Velocity:
- Let the initial velocity of the ball be u.
- The vertical component of the velocity before the impact is usinα.
- The horizontal component of the velocity before the impact is ucosα.
- After rebounding, the vertical component of the velocity is vsinβ and the horizontal component is vcosβ.
3. Applying the Conservation of Momentum:
- Since the floor is smooth, the horizontal momentum is conserved. Therefore, the horizontal components of the velocities before and after the collision are equal:
ucosα=vcosβ
- This gives us our first equation.
4. Using the Coefficient of Restitution:
- The coefficient of restitution (e) is defined as the ratio of the relative speed after the collision to the relative speed before the collision along the normal direction:
e=Velocity of separationVelocity of approach=vsinβusinα
- Rearranging this gives:
vsinβ=e⋅usinα
5. Combining the Equations:
- From the first equation, we can express v in terms of u:
v=ucosαcosβ
- Substitute this expression for v into the equation for the coefficient of restitution:
ucosαcosβsinβ=e⋅usinα
- Cancel u from both sides (assuming u≠0):
cosαsinβcosβ=esinα
6. Rearranging to Find Relation:
- Rearranging gives:
tanβ=esinαcosα
- This simplifies to:
tanβ=etanα
Final Relation:
Thus, the relation between the angles α and β is:
tanβ=etanα
- A ball strikes the floor at an angle α with the normal (the line perpendicular to the surface).
- After rebounding, it moves at an angle β with the normal.
- The coefficient of restitution (e) relates the velocities before and after the collision.
- Let the initial velocity of the ball be u.
- The vertical component of the velocity before the impact is usinα.
- The horizontal component of the velocity before the impact is ucosα.
- After rebounding, the vertical component of the velocity is vsinβ and the horizontal component is vcosβ.
- Since the floor is smooth, the horizontal momentum is conserved. Therefore, the horizontal components of the velocities before and after the collision are equal:
ucosα=vcosβ
- This gives us our first equation.
- The coefficient of restitution (e) is defined as the ratio of the relative speed after the collision to the relative speed before the collision along the normal direction:
e=Velocity of separationVelocity of approach=vsinβusinα
- Rearranging this gives:
vsinβ=e⋅usinα
- From the first equation, we can express v in terms of u:
v=ucosαcosβ
- Substitute this expression for v into the equation for the coefficient of restitution:
ucosαcosβsinβ=e⋅usinα
- Cancel u from both sides (assuming u≠0):
cosαsinβcosβ=esinα
- Rearranging gives:
tanβ=esinαcosα
- This simplifies to:
tanβ=etanα
Thus, the relation between the angles α and β is:
tanβ=etanα
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:NCERT FILE (NCERT Textbook Exercise)
Explore 23 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:NCERT FILE (NCERT Additional Exercise)
Explore 7 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Conceptual Questions
Explore 20 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
A particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown

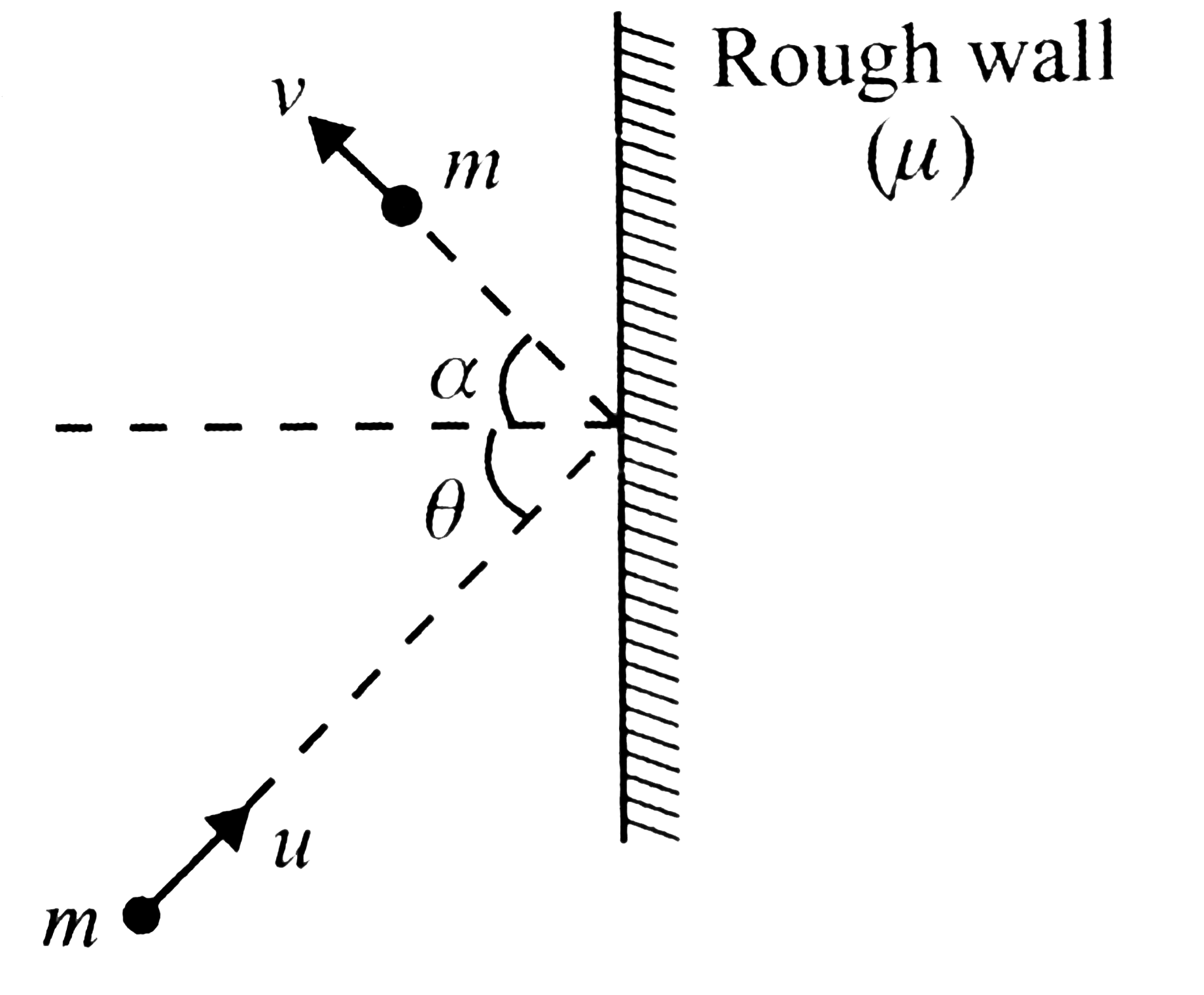
View SolutionA small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
View Solution
Knowledge Check
A ball moving with velocity u strikes a smooth horizontal floor at an angle α with the normal to the surface at the point of contact . After collision , ball moves with velocity v at an angle β with the normal . Assume e as the coefficient of restitution .
Atanα=etanβBImpulse applied by the surface on the ball is mu(1+e)cosCv=u√(sin2α+e2cos2α)Dv=tanαA ball strikes a smooth horizontal floor obliquely and rebounds inelastically.
AThe kinetic energy of the ball just after hitting the floor is equal to the potential energy of the ball at its maximum height alter rebound.BTotal energy of the ball is not conserved.CThe angle of rebound with the vertical is greater than the angle of incidence.DNone of the above.A ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
A(θ+β)<90∘ if the wall is smoothBif the wall is rough , coefficient of restitution =tanβ/cosθCif the wall is rough, coefficient of restition
<tanβ/cotθDnone of these
A body projected at an angle α to the horizontal lands at the same point after hitting a verticle wall. This time it makes an angle β with the horizontal. Show that etanβ=tanα where e is the coefficient of restitution between the body and the wall.
View SolutionA particle is thrown with speed u at an angle α with horizontal from the ground. After how much time, the velocity of particle will make an angle β with horizontal.
View SolutionA ball strickes a horizontal floor at an angle θ=45∘ with the normal to floor. The coefficient of restitution between the ball and the floor is e=1/2. The function of its kinetic energy lost in the collision is.
View SolutionA ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is

View SolutionA particle strikes a horizontal smooth floor with a velocity u making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. The coefficient of restitution between the particle and the floor is e.
View Solution
