A bead of mass m is fitted on to a rod and can move on it without friction. At the initial moment the bead is in the middle of the rod. The rod moves translationally in a horizontal plane with an acceleration a in a direction forming an angle α with the rod. Find the acceleration of the bead relative to the rod.

g sin α
(g+a0)sinα
gsinα+a0cosα
gsinα−a0cosα
The correct Answer is:D

mg sin α - ma0cosα=ma
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:More than one correct
Explore 18 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Assertion - Reason
Explore 12 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Problem For Practice
Explore 23 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Comprehension type Queston
Explore 14 Videos
Similar Questions
A uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
( c) Find normal contact force due to hinge when rod has rotated through angle θ as shown in Fig.
View SolutionIn the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
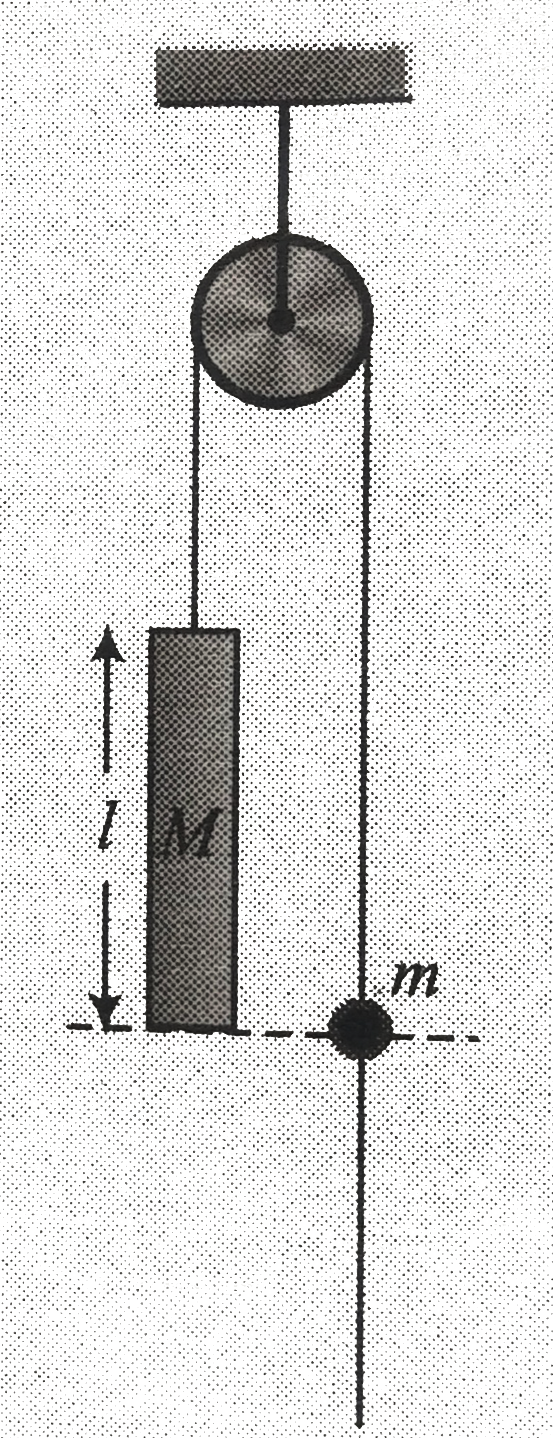
View Solution
Knowledge Check
A bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
zAgsinαB(g+a0)sinαCgsinα+a0cosαDgsinα−a0cosαA bead of mass m moves on a rod without friction. Initially the bead is at the middle of the rod and the rod moves translationally in a vertical plane with an acceleration a0 in a direction forming angle θ with the horizontal as shown in the given figure. The acceleration of bead with respect to rod is
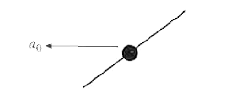 AgsinθB(g+a0)sinθCgsinθ+a0cosθDgsinθ−a0cosθ
AgsinθB(g+a0)sinθCgsinθ+a0cosθDgsinθ−a0cosθA rod touches a disc kept on a smooth horizontal plane. If the rod moves with an acceleration a, the disc rolls on the rod without acceleration a, the disc rools on therod without slidding. Then , the acceleration of the disc w.r.t the rod is
 Aa3B√3a2CzeroDa/2
Aa3B√3a2CzeroDa/2
A long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping is
View SolutionA rod of mass 'm and length L is attached to a L shaped plank at 'A'. rod can move freely about A. A string is tied between rod and plank as shown in figure. Whole system is moving with a constant acceleration g in x-direction

If string is cut at any instant then the angular acceleration of rod (with respect to the plank) at that instant is
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
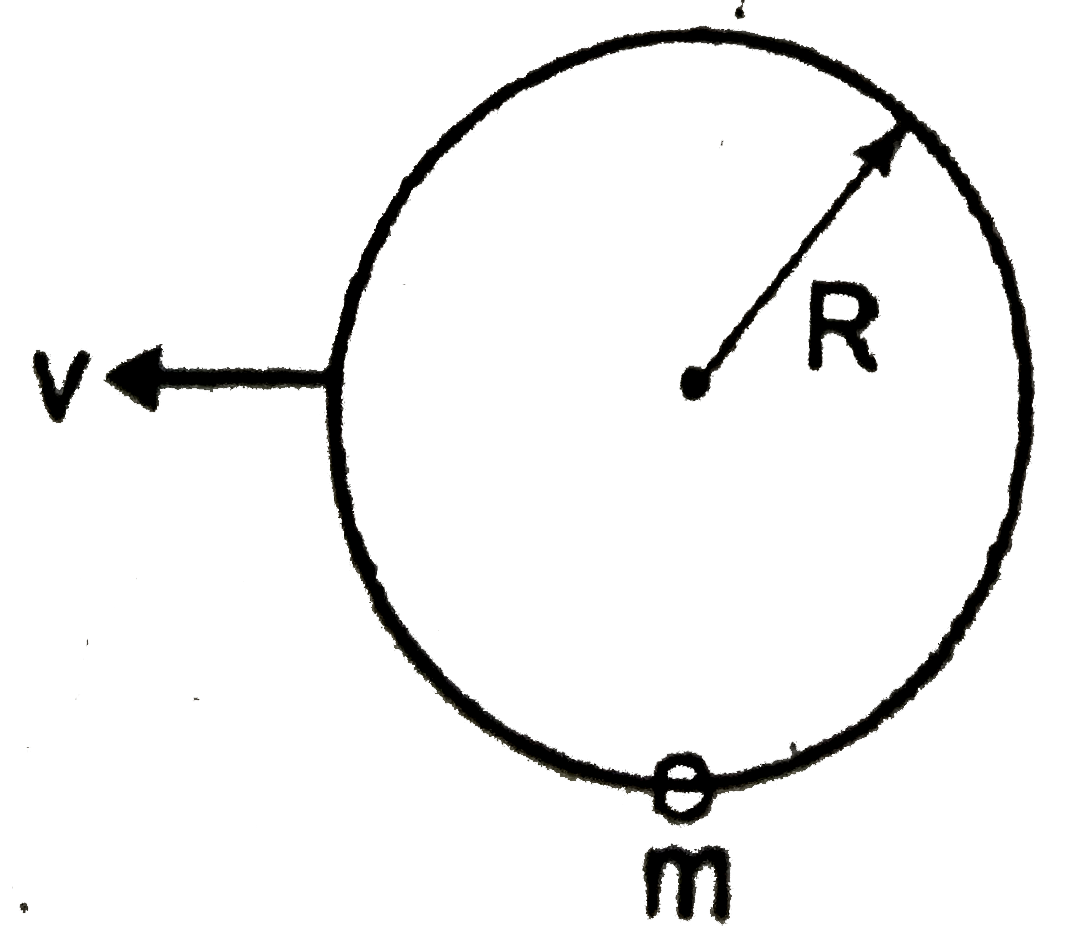
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of level arm I. One force is of magnitude F and acts at one extreme end. The length of the rod is
View Solution