A block A kept on an inclined surface just begins to slide if the inclination is 300. The block is replaced by another block B and it is found that it just begins to slide if the inclination is 400
mass of A > mass of B
mass of A < mass of B
mass of A=mass of B
all the three are possible.
The correct Answer is:D
To solve the problem, we need to analyze the situation using the principles of friction and the forces acting on the blocks on an inclined plane.
1. Understanding the Problem:
- Block A begins to slide at an angle of inclination of 30∘.
- Block B begins to slide at an angle of inclination of 40∘.
- We need to determine the relationship between the masses of blocks A and B.
2. Identifying the Forces:
- When a block is on an inclined surface, the forces acting on it include gravitational force and frictional force.
- The component of gravitational force acting down the incline is given by mgsinθ, and the frictional force opposing this motion is given by f=μN, where N is the normal force.
3. Calculating the Normal Force:
- The normal force N on an inclined plane is given by N=mgcosθ.
- Thus, the frictional force can be expressed as f=μmgcosθ.
4. Setting Up the Condition for Sliding:
- A block will begin to slide when the gravitational component down the incline equals the maximum static frictional force:
mgsinθ=μmgcosθ
- This simplifies to:
tanθ=μ
5. Applying the Condition for Both Blocks:
- For block A at 30∘:
tan30∘=μA⇒μA=1√3≈0.577
- For block B at 40∘:
tan40∘=μB⇒μB≈0.839
6. Comparing the Coefficients of Friction:
- Since μB>μA, this indicates that block B has a greater coefficient of friction than block A.
7. Conclusion on Mass Relationship:
- The angle of inclination at which a block begins to slide is independent of its mass. Therefore, we cannot determine the mass relationship based solely on the angles at which the blocks slide.
- Thus, all three options regarding the mass of A and B are possible:
- Mass of A is greater than mass of B.
- Mass of A is less than mass of B.
- Mass of A equals mass of B.
8. Final Answer:
- The correct option is that all three conditions regarding the masses are possible.
- Block A begins to slide at an angle of inclination of 30∘.
- Block B begins to slide at an angle of inclination of 40∘.
- We need to determine the relationship between the masses of blocks A and B.
- When a block is on an inclined surface, the forces acting on it include gravitational force and frictional force.
- The component of gravitational force acting down the incline is given by mgsinθ, and the frictional force opposing this motion is given by f=μN, where N is the normal force.
- The normal force N on an inclined plane is given by N=mgcosθ.
- Thus, the frictional force can be expressed as f=μmgcosθ.
- A block will begin to slide when the gravitational component down the incline equals the maximum static frictional force:
mgsinθ=μmgcosθ
- This simplifies to:
tanθ=μ
- For block A at 30∘:
tan30∘=μA⇒μA=1√3≈0.577
- For block B at 40∘:
tan40∘=μB⇒μB≈0.839
- Since μB>μA, this indicates that block B has a greater coefficient of friction than block A.
- The angle of inclination at which a block begins to slide is independent of its mass. Therefore, we cannot determine the mass relationship based solely on the angles at which the blocks slide.
- Thus, all three options regarding the mass of A and B are possible:
- Mass of A is greater than mass of B.
- Mass of A is less than mass of B.
- Mass of A equals mass of B.
- The correct option is that all three conditions regarding the masses are possible.
Topper's Solved these Questions
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Objective -2
5 Videos
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Exercises
31 Videos
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - worked out Examples
10 Videos
- FLUID MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions
90 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers
18 Videos
Similar Questions
A block is kept on a frictionless inclined surface with angle of inclination α. The incline is given an acceleration 'a' to keep the block stationary. Then a is equal to
View SolutionA block of mass 5 kg is at rest on a rough inclined surface. If angle of inclination of plane is 60∘, then force applied by it on block is
View SolutionA wooden block is placed on an inclined plane. The block just begins to slide down when the angle of the inclination is increased to 45°. What is the coefficient of the friction?
View SolutionA block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
View SolutionThe time taken for an ice block to slide down on inclined surface of inclination 60∘ is 1-2 times the time taken by the same ice block to slide down a frictionless inclined plane of the same inclination. Calculate the coefficient of friction between ice and the inclined plane ?
View SolutionA block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is

View SolutionFigure shown two blocks in contact sliding down an inclined surface of inclination 30∘. The friction coefficient between block of mass 2kgand the incline is μ1=0.20 and that between the block of mass 4kg and the incline is μ2=0.30 .Find the acceleration of 2.0kg block g=10ms−2

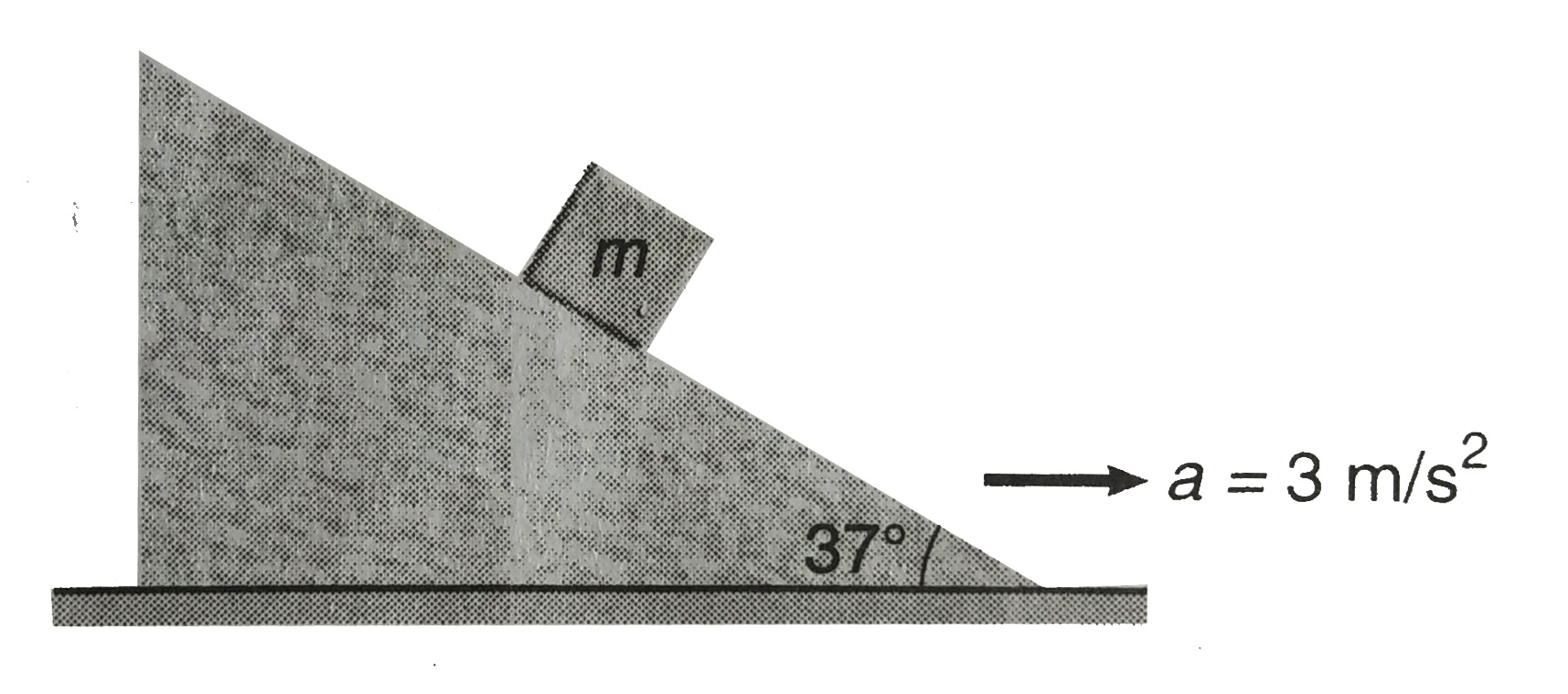
View SolutionA block is placed on an inclined plane as shown in figure. What must be the friction force between block and inclined if the block is not to slide along the inclined when the incline is accelerating to the right at 3m/s2(sin37∘=35)? (Takeg=10m/s2)
View SolutionA block is kept on a inclined plane of inclination θ of length l. The velocity of particle at the bottom of inclined is (the coefficient of friction is μ
View SolutionA block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friciton is μ)
View Solution
