The time taken for an ice block to slide down on inclined surface of inclination 60∘ is 1-2 times the time taken by the same ice block to slide down a frictionless inclined plane of the same inclination. Calculate the coefficient of friction between ice and the inclined plane ?
To solve the problem of finding the coefficient of friction between the ice block and the inclined plane, we can follow these steps:
1. Identify the Given Information:
- Inclination angle, θ=60∘
- The time taken for the ice block to slide down the inclined surface with friction is t=12T (where T is the time taken on a frictionless plane).
2. Free Body Diagram Analysis:
- For the frictionless inclined plane:
- The only force acting along the incline is the component of gravitational force: Fgravity=mgsinθ.
- The acceleration a2 of the block down the frictionless incline is given by:
a2=gsinθ
- For the inclined plane with friction:
- The forces acting are the gravitational component down the incline and the frictional force opposing the motion.
- The net force is:
Fnet=mgsinθ−Fr
- Where Fr=μmgcosθ (frictional force).
- The acceleration a1 of the block down the incline with friction is given by:
a1=gsinθ−μgcosθ
3. Using the Kinematic Equation:
- For the frictionless incline:
s=12a2T2⇒s=12(gsinθ)T2
- For the inclined plane with friction:
s=12a1t2⇒s=12(gsinθ−μgcosθ)(T2)2
s=12(gsinθ−μgcosθ)T24=18(gsinθ−μgcosθ)T2
4. Equating the Distances:
- Since both expressions for s represent the same distance:
12(gsinθ)T2=18(gsinθ−μgcosθ)T2
- Cancel T2 from both sides (assuming T≠0):
4gsinθ=gsinθ−μgcosθ
5. Rearranging the Equation:
- Rearranging gives:
4gsinθ−gsinθ=−μgcosθ
3gsinθ=−μgcosθ
- Dividing by g (assuming g≠0):
3sinθ=−μcosθ
- Rearranging gives:
μ=−3sinθcosθ
6. Calculating the Coefficient of Friction:
- Substitute θ=60∘:
μ=−3sin60∘cos60∘=−3⋅√3212=−3√3
- Since the coefficient of friction cannot be negative, we take the positive value:
μ=3√32
Final Answer:
The coefficient of friction between the ice and the inclined plane is μ=3√32.
- Inclination angle, θ=60∘
- The time taken for the ice block to slide down the inclined surface with friction is t=12T (where T is the time taken on a frictionless plane).
- For the frictionless inclined plane:
- The only force acting along the incline is the component of gravitational force: Fgravity=mgsinθ.
- The acceleration a2 of the block down the frictionless incline is given by:
a2=gsinθ
- The forces acting are the gravitational component down the incline and the frictional force opposing the motion.
- The net force is:
Fnet=mgsinθ−Fr
- Where Fr=μmgcosθ (frictional force).
- The acceleration a1 of the block down the incline with friction is given by:
a1=gsinθ−μgcosθ
- For the frictionless incline:
s=12a2T2⇒s=12(gsinθ)T2
- For the inclined plane with friction:
s=12a1t2⇒s=12(gsinθ−μgcosθ)(T2)2
s=12(gsinθ−μgcosθ)T24=18(gsinθ−μgcosθ)T2
- Since both expressions for s represent the same distance:
12(gsinθ)T2=18(gsinθ−μgcosθ)T2
- Cancel T2 from both sides (assuming T≠0):
4gsinθ=gsinθ−μgcosθ
- Rearranging gives:
4gsinθ−gsinθ=−μgcosθ
3gsinθ=−μgcosθ
- Dividing by g (assuming g≠0):
3sinθ=−μcosθ
- Rearranging gives:
μ=−3sinθcosθ
- Substitute θ=60∘:
μ=−3sin60∘cos60∘=−3⋅√3212=−3√3
- Since the coefficient of friction cannot be negative, we take the positive value:
μ=3√32
The coefficient of friction between the ice and the inclined plane is μ=3√32.
Topper's Solved these Questions
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Additional solved examples
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Conceptual short answer questions with answer
9 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- GRAVITATIONBOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP
2 Videos
Similar Questions
Knowledge Check
Starting from rest, a body slides down a 45∘ inclined plane in twice the time it itakes to slide the same distance in the absence of friction.
They the coefficient of friction between the body and the inclined plane isA1/4B2/3C3/4D√3/2
A piece of ice slides down a 45∘ incline in twice the time it takes to slide down a frictionless 45∘ incline . What is the coefficient of friction between the ice and the incline ? .
View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination θ and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
View SolutionStarting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View SolutionTwo identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
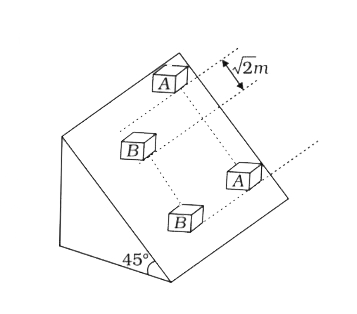
View SolutionA given object taken n time more time to slide down 45∘ rough inclined plane as it taken to slide down a perfectly smooth 45∘ incline The coefficient of kintic friction between the object and the incline is .
View Solution

