A block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
4cm
5cm
10 cm
16 cm
The correct Answer is:B
To solve the problem, we need to find the maximum amplitude of the plank in which the block does not slip over it, given the coefficient of friction, angular frequency, and gravitational acceleration.
1. Identify Given Values:
- Coefficient of friction (μ) = 1/2
- Angular frequency (ω) = 10 rad/s
- Gravitational acceleration (g) = 10 m/s²
2. Understand the Condition for No Slipping:
- For the block to not slip over the plank, the maximum static friction must be equal to the pseudo force acting on the block due to the acceleration of the plank.
3. Calculate Maximum Acceleration of the Plank:
- The maximum acceleration (a_max) of the plank during SHM can be calculated using the formula:
amax=ω2A
- Here, A is the maximum amplitude we need to find.
4. Set Up the Equation for No Slipping:
- The force of friction (F_friction) that prevents slipping is given by:
Ffriction=μN
- The normal force (N) acting on the block is equal to its weight (mg):
N=mg
- Therefore, the friction force can be expressed as:
Ffriction=μmg
5. Relate Friction Force to Pseudo Force:
- The pseudo force acting on the block due to the acceleration of the plank is:
Fpseudo=mamax
- For no slipping, we set the friction force equal to the pseudo force:
μmg=mamax
6. Cancel Mass (m) from Both Sides:
- We can cancel mass (m) from both sides of the equation:
μg=amax
7. Substitute Values:
- Substitute the known values into the equation:
12⋅10=amax
- This gives:
amax=5 m/s2
8. Relate Maximum Acceleration to Amplitude:
- Now, we can relate this back to the maximum amplitude:
amax=ω2A
- Rearranging gives:
A=amaxω2
9. Calculate Maximum Amplitude:
- Substitute the values of amax and ω:
A=5102=5100=0.05 m
- Converting to centimeters:
A=5 cm
Final Answer:
The maximum amplitude of the plank in which the block does not slip over it is 5 cm.
- Coefficient of friction (μ) = 1/2
- Angular frequency (ω) = 10 rad/s
- Gravitational acceleration (g) = 10 m/s²
- For the block to not slip over the plank, the maximum static friction must be equal to the pseudo force acting on the block due to the acceleration of the plank.
- The maximum acceleration (a_max) of the plank during SHM can be calculated using the formula:
amax=ω2A
- Here, A is the maximum amplitude we need to find.
- The force of friction (F_friction) that prevents slipping is given by:
Ffriction=μN
- The normal force (N) acting on the block is equal to its weight (mg):
N=mg
- Therefore, the friction force can be expressed as:
Ffriction=μmg
- The pseudo force acting on the block due to the acceleration of the plank is:
Fpseudo=mamax
- For no slipping, we set the friction force equal to the pseudo force:
μmg=mamax
- We can cancel mass (m) from both sides of the equation:
μg=amax
- Substitute the known values into the equation:
12⋅10=amax
- This gives:
amax=5 m/s2
- Now, we can relate this back to the maximum amplitude:
amax=ω2A
- Rearranging gives:
A=amaxω2
- Substitute the values of amax and ω:
A=5102=5100=0.05 m
- Converting to centimeters:
A=5 cm
The maximum amplitude of the plank in which the block does not slip over it is 5 cm.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Only one question is correct
48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
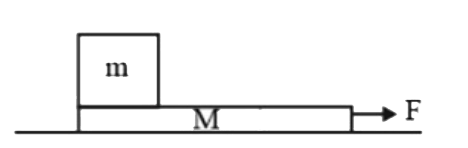
A bolck of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface g=10ms−1
View SolutionA block is placed over a plank. The coefficient of friction between the block and the plank is μ=0.2. Initially both are at rest, suddenly the plank starts moving with acceleration a0=4m/s2. The displacement of the block in 1 is (g=10m/s2)
View SolutionA block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
View SolutionA block of mass M=4kg of height and breath b is placed on a rough plank of same mass M. A light inextensible string is connected to the upper end of the block and passed through a light smooth pulley as shown in figure. A mass m=1kg is hung to the other end of the string.
a. What should be the minimum value of coefficient of friction between the block and the plank so that, there is no slipping between the block and the wedge?
b. Find the minimum value of b/h so that the block does not topple over the plank, friction is absent between the plank and the ground.

View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA block of mass m kept on rough horizontal turn table at a distance x from the centre. If the coefficient of friction between the table and block is μ then maximum speed of point P on turn table so that the block does not slip is

View SolutionA small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
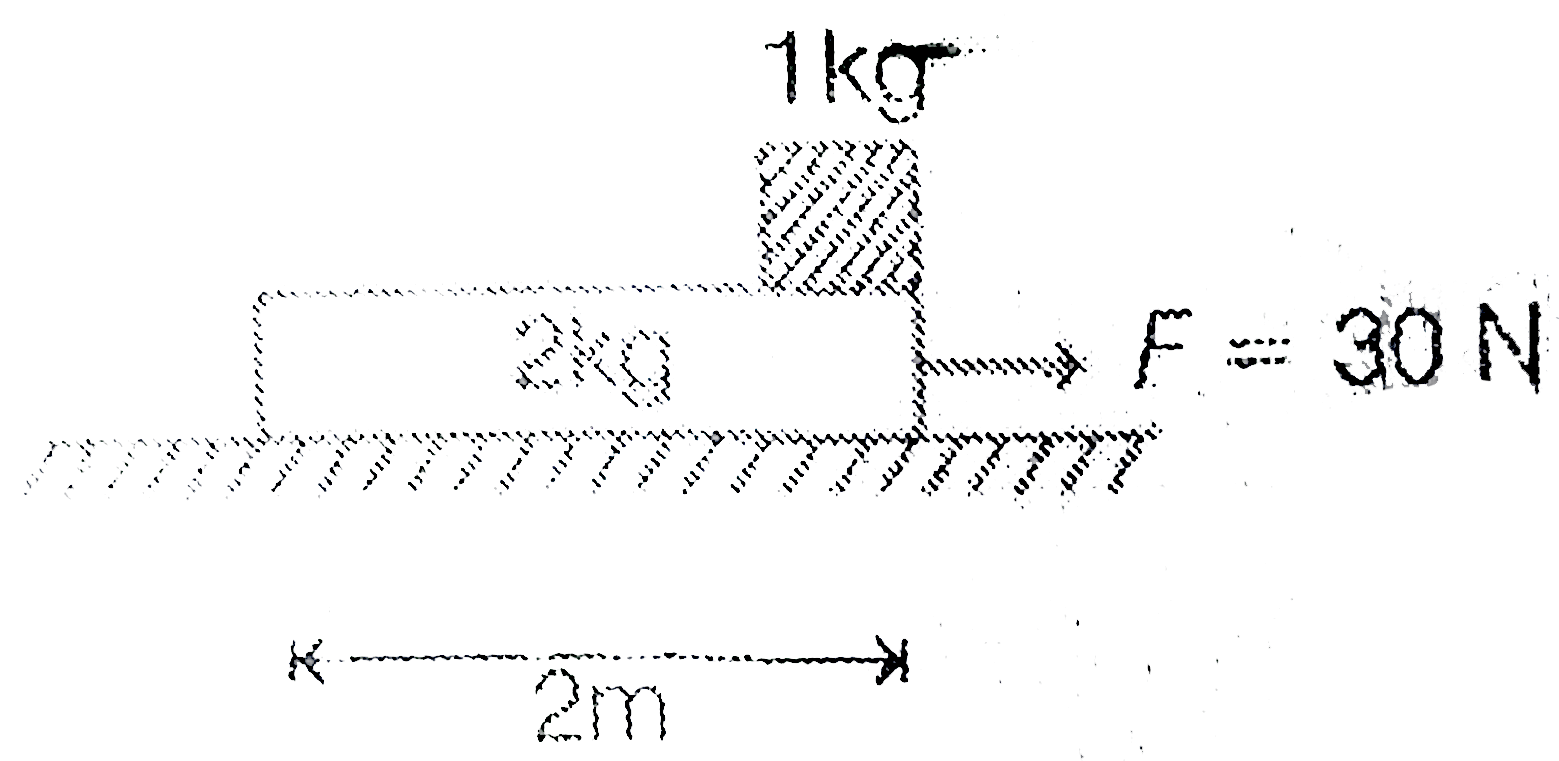
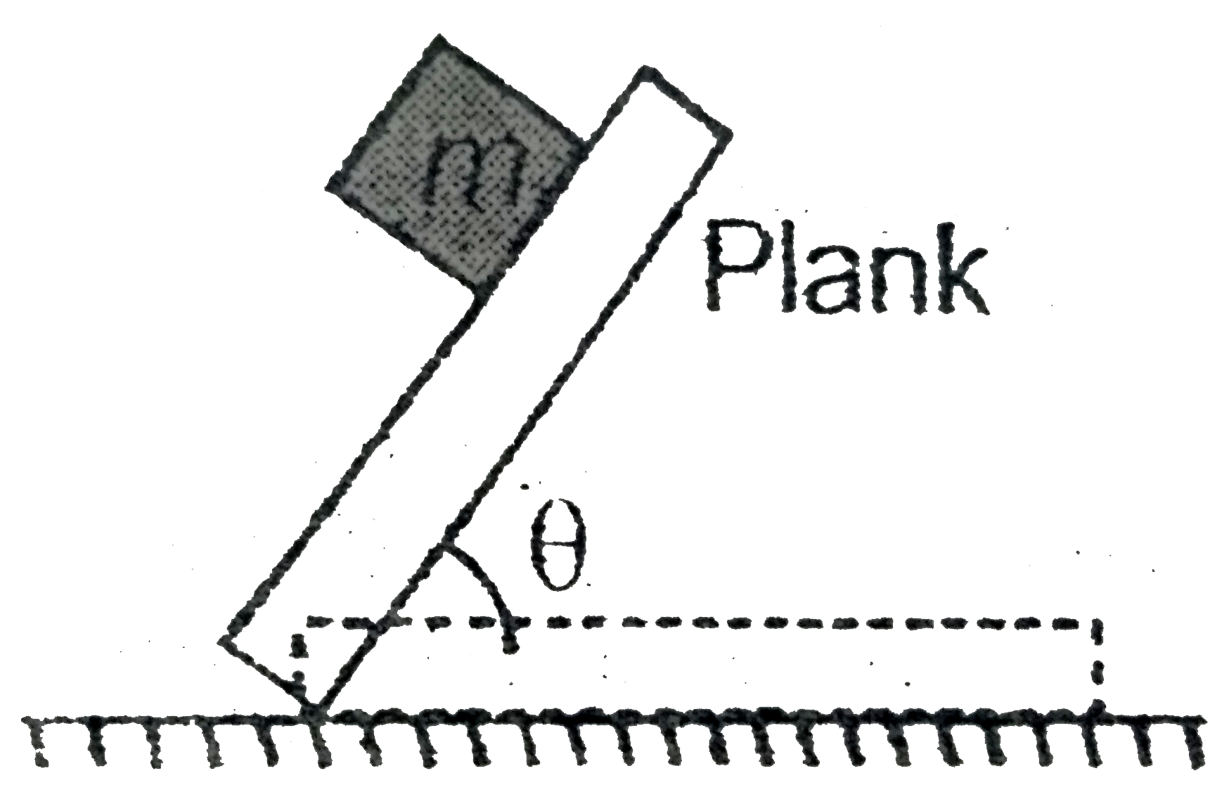
View SolutionA block of mass m is kept on a plank . The coefficient of friction between the plank and block is 1. The plank is slowly raised from one end so that it makes angle θ with horizontal . The forces of friction acting on the plank , when θ=30∘andθ60∘ are respectively,
View Solution
