A block of ice starts sliding down from the top of the inclined roof of a house (angle of inclination of roof=30∘ with the horizontal) along aline of maximum slope. The highest and lowest points of the roof are at heights of 8.1m and 5.6 m respectively from the ground. At what horizontal distance from the starting point will the block hit the ground? Neglect friction.
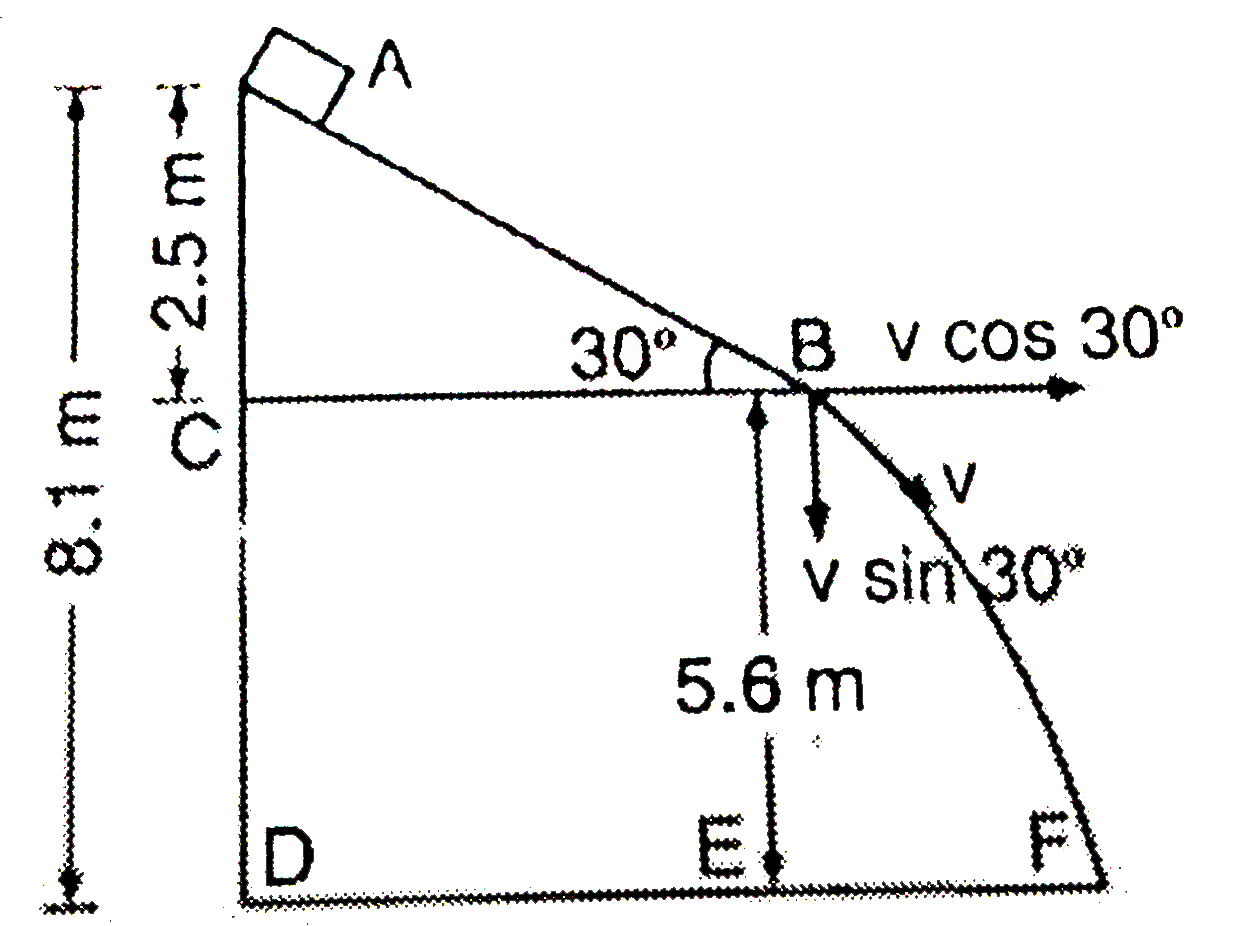
When the ice block silides down from A to B, it falls vertically through AC=2.5m
If v is the velocity with which it reaches B, then v2=u2+2as, where u=0,a=gsin30∘ and s=AB.
∴v2=2g×ACAB×AB(sin30∘=ACAB)
=2×9.8×2.5=49
∴v=7ms−1 along AB, Resolve this velocity v into:
(i) a horizontal component
=vcos30∘=7×(√3/2)=3.5×√3ms−1
Vertical motion:
Let t be the time taken by the block to reach the ground.
Apply s=ut+12gt2
Given s=5.6m,u=3.5ms−1,g=9.8ms−2
∴5.6=3.5t+12×9.8t2 or 4.9t2+3.5t−5.6=0
Dividing this equation by 0.7, we get 7t2+5t−8=0
∴t=−5+0√(5)2+(4×7×8)2×7
∴t=−5±15.7814
Rejecting the -ve value,
=−5+15.7814=10.7814=0.77s
Horizontal Motion:
Horizontal distance travelled EF
=Horizontal velocity xx time
=3.5×√3×0.77=4.668m
∴ Total horizontal distance =DF=DE+EF
=4.33+4.668=8.998m
(DE=BC=ACcot30∘=2.5×√3=4.33m)
Topper's Solved these Questions
Similar Questions
A particle is thrown horizontally from the top of an inclined plane , with a speed of 5m/s . If the inclination of the plane is 30∘ with the horizontal , how far from the point of projection will the particle strike the plane ?
View SolutionHeight of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
View Solution
Knowledge Check
A ball is thrown from a point in level with velocity u and at a horizontal distance r from the top of a tower of height h.
At what horizontal distance x from the foot of the tower does the ball hit the ground ? Aucosθg{(u2sin2θ+gh)1/2−usinθ}Bucosθg{(u2cos2θ+2gh)1/2−ucosθ}Cucosθg{(u2cos2θ+gh)1/2−ucosθ}Ducosθg{(u2cos2θ+gh)1/2−ucosθ}
Aucosθg{(u2sin2θ+gh)1/2−usinθ}Bucosθg{(u2cos2θ+2gh)1/2−ucosθ}Cucosθg{(u2cos2θ+gh)1/2−ucosθ}Ducosθg{(u2cos2θ+gh)1/2−ucosθ}A boy playing on the roof of a 10m high building throws a ball with a speed of 10m/s at an angle of 30(∘) with the horizontal. How far from the throwing point will the ball be at the height of 10m from the ground ?
[g=10m/s2,sin30∘=12,cos30∘=√32]A5.2mB4.33mC2.66mD8.66mA block is projected upwards with a velocity of 5 m/s from the bottom of a rough inclined plane of inclination 30° with the horizontal. It stops after 0.5 s. What is the coefficient of friction ? (g=10m/s2)
A√3B1√3C√2D√5
A rupee coin, starting from rest rolls down a distance of 1 m on a plane inclined at an angle of 30∘ with the horizontal. Assuming that g=9.81ms−2, time taken is : -
View SolutionA block is at rest at the top of a rough inclined plane of inclination 30° with the horizontal. What is the coefficient of kinetic friction between the block and the plane, if the . block slides down with an acceleration of g5 ?
View SolutionWhat is the time required for a block to slide down from the top to the bottom ofan inclined plane 6.4 m long if the inclination of the plane with the horizonta l is 30° and the coefficient of friction= 0.2?
View SolutionTwo bodies slide from rest down two smooth inclined planes commencing at the same point and terminating in the same horizontal plane. The ratio of the velocities attained if inclinations to the horizontal of the planes are 30∘ and 60∘ respectively is
View SolutionAn arrow is shot horizontally from a height of 4.9 m above the ground. The initial speed of the arrow is 45 m/s. Neglecting friction, how long will it take the arrow to hit the ground?
View Solution
