A block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:
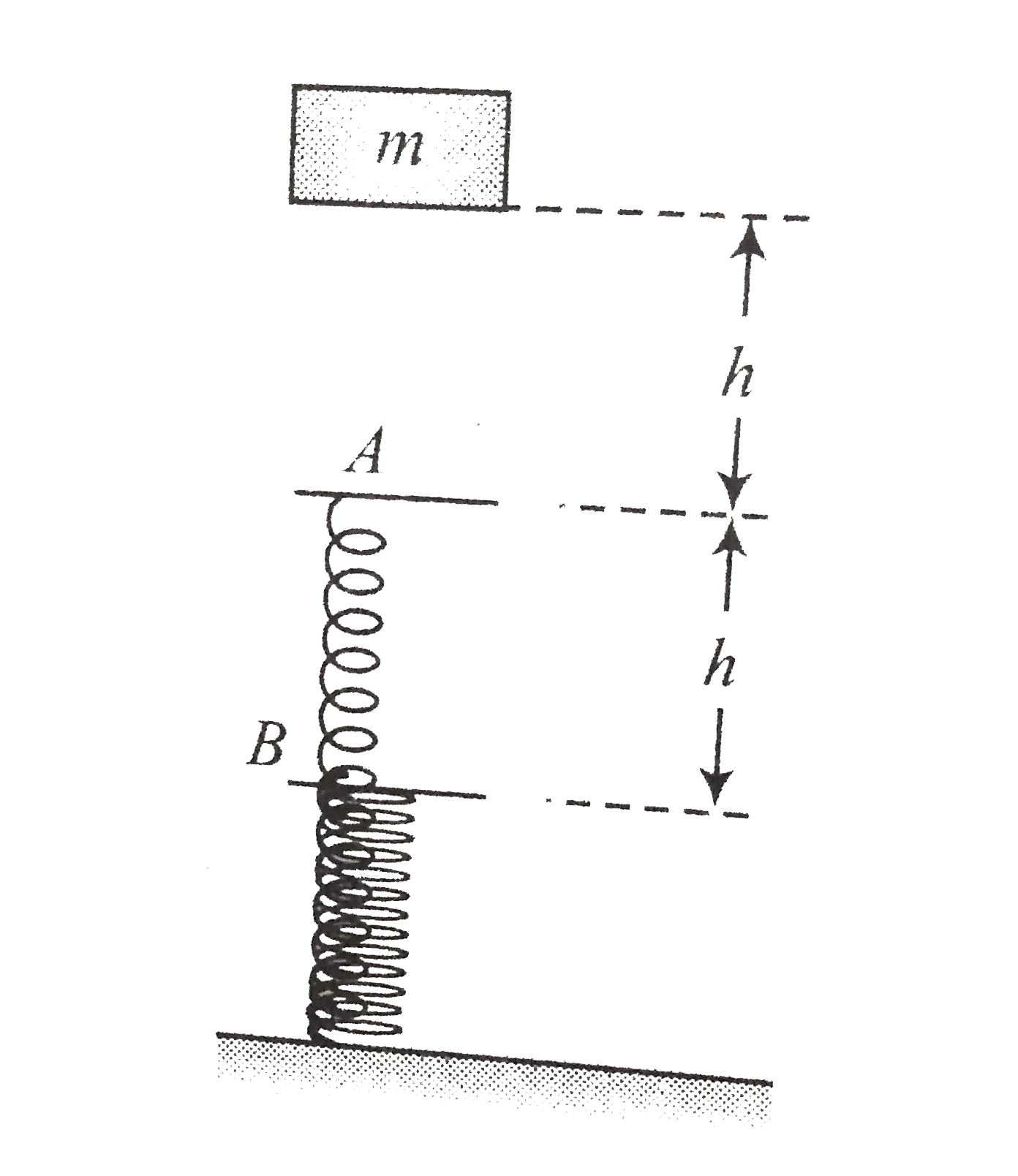
a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block
The correct Answer is:a. 4mgh; b. h9; c. 43√2gh; d. 4g↑
a. mg3h=12kA(2h)2+12kBh2

Put kA=mg2h
And solve to get kB=4mgh
b. mg=kA(h+x)+kBξmpliesx=h9
c. Maximum velocity will be at equilibrium position.
mg(h+h+x)=12mv2max+12kA(h+x)2+12kBx2

Solve to get vmax=43√2gh
d. Maximum acceleration will be at M:
amax=kA2h+kBh−mgm=4g↑⏐
⏐⏐
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

View SolutionA block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
View Solution
Knowledge Check
A block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
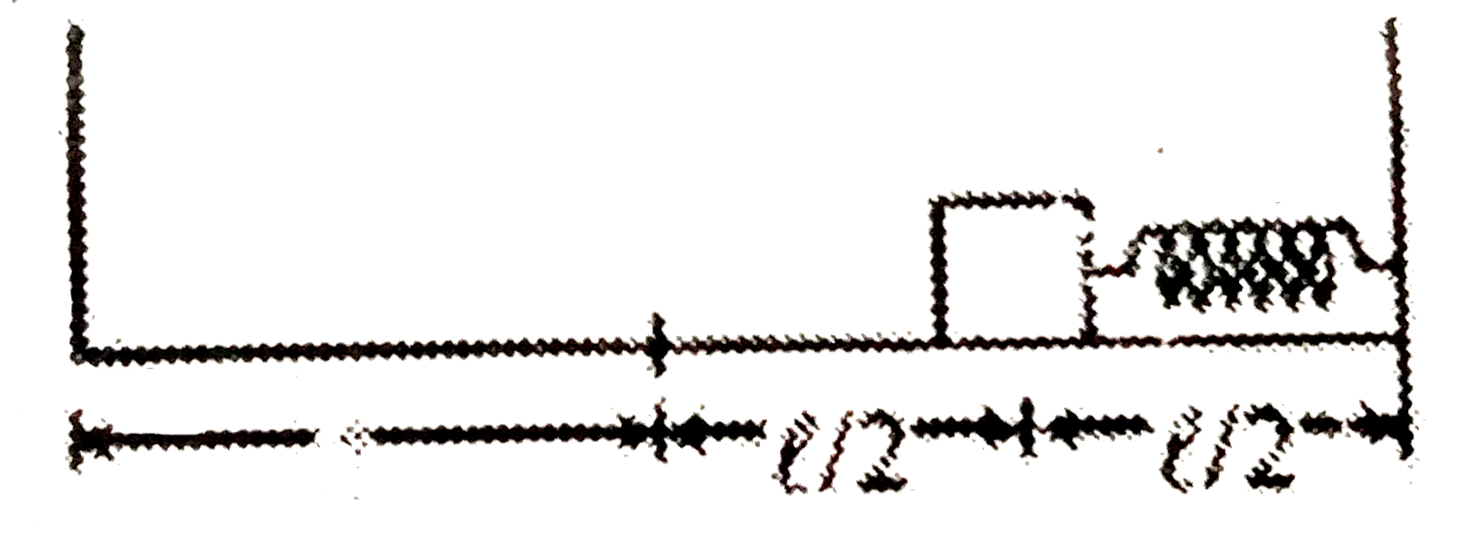 A2π√mkB(π+4)√mkC(1+π)√mkDNone of these
A2π√mkB(π+4)√mkC(1+π)√mkDNone of theseA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2
A block of mass m is suddenly released from the top of a spring of stiffness constant k.
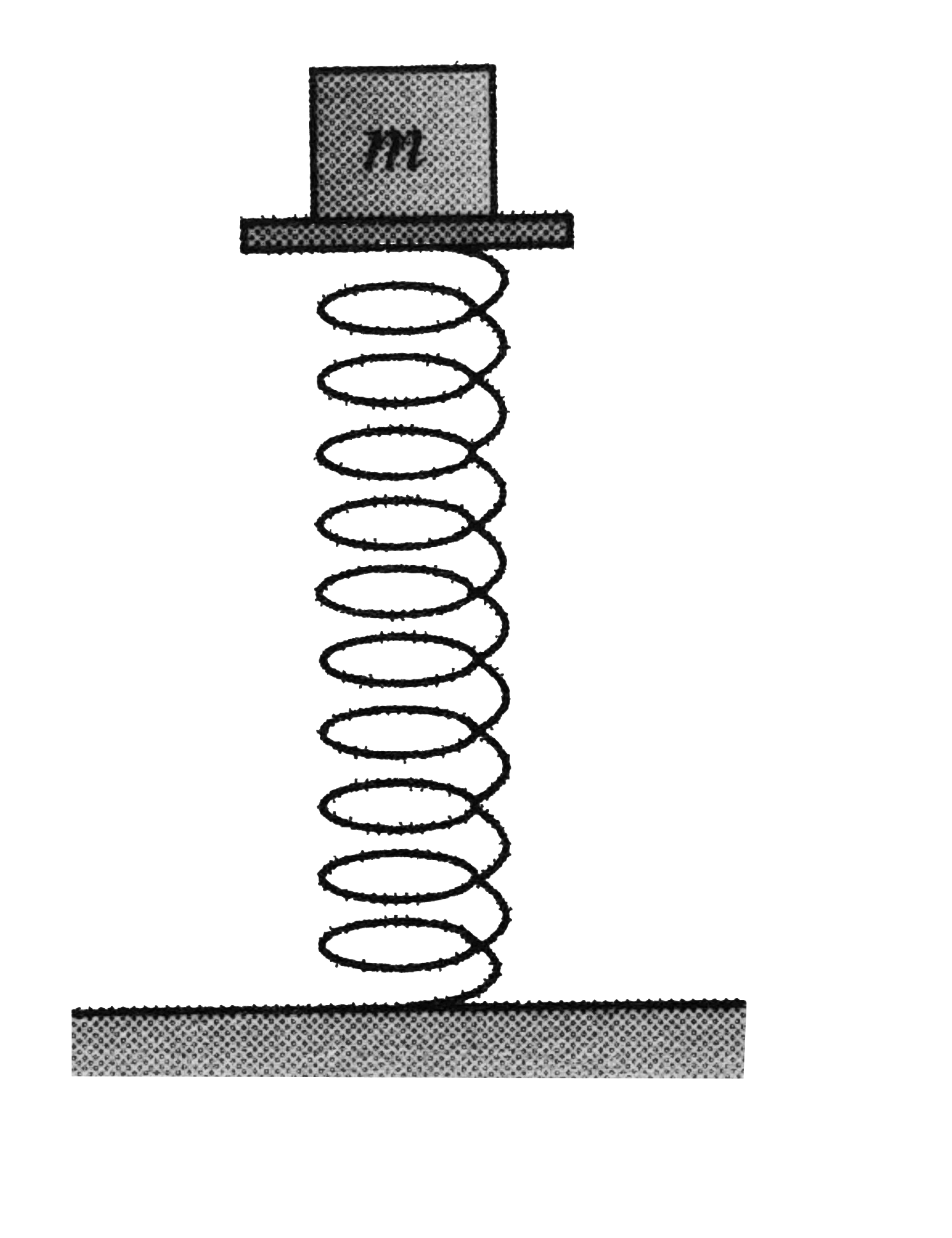
a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View SolutionA block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View SolutionA block of mass m is relesed from rest from a height h onto a smooth sledge of mass M fitted with an ideal spring of stiffness k.

View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionA 10 kg metal block is attached to a spring constant 1000Nm−1. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
View Solution
