A block of mass m resting on a smooth horizontal plane starts moving due to a constant force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle θ varies as θ=λs, where λ is constant and s is the distance traversed by the block from its intial position. Find the velocity of the block as a function of the angle θ. Also show that the block will never lose contact with the ground.
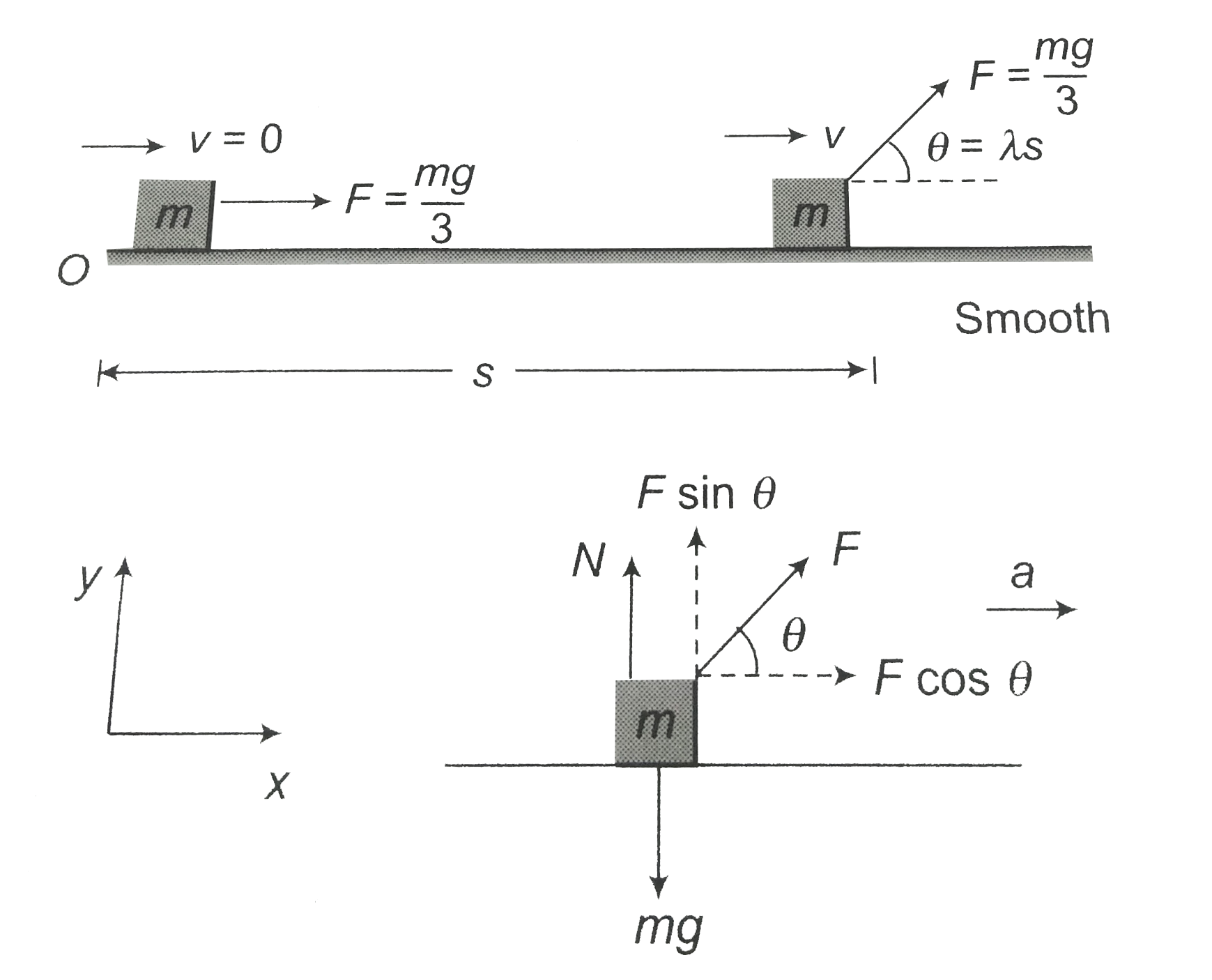
x−direction: Fcosθ=ma
a=Fmcosθ=mgcos(λs)3m
vdvdx=g3cos(λs)
∫v0vdv=83∫s0cos(λs)ds
∣∣∣v22∣∣∣v0=g3|sin(λs)|s0λ
v2=2g3λsin(λs)
v=√2gsinθ3λ
y−direction: N+Fsinθ=mg
N=mg−mg3sinθ
(sinθ)max=1,Nmin=2mg3
Since normal reaction will never will never be zero and hence the block will never lose constact with the ground.
Topper's Solved these Questions
Similar Questions
A bar of mass m resting on a smooth horizontal plane starts moving due to the force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle α between the direction of this force and the horizontal varies as α=as, where a is a constant, and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle α.
View SolutionA bar of mass m resting on a smooth horizontal plane starts moving due to the force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle α between the direction of this force and the horizontal varies as α=as, where a is a constant, and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle α.
View Solution
Knowledge Check
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθA force F of constant magnitude acts on a block of mass 'm' and t=0,initially along positive x-direction. The direction of force F starts rotating with a constant angular velocity ω in anticlockwise sense. Then the magnitude of velocity of the block as a function of time 't' is ( initial block was at rest )
AFmωsin(ωt2)B2Fmωsin(ωt2)CF2mωsin(ωt2)D2F3mωsin(ωt2)A block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.
 AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)
AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)
The block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA force F of constant magnitude acts on a block of mass 'm' and t=0,initially along positive x-direction. The direction of force F starts rotating with a constant angular velocity ω in anticlockwise sense. Then the magnitude of velocity of the block as a function of time 't' is ( initial block was at rest )
View Solution
