A block released from rest from the top of a smooth inclined plane of angle θ1 reaches the bottom in time t1. The same block released from rest from the top of another smooth inclined plane of angle θ2 reaches the bottom in time t2 If the two inclined planes have the same height, the relation between t1andt2 is
t2t1=(sinθ1sinθ2)1/2
t2t1=1
t2t1=sinθ1sinθ2
t2t1=sin2θ1sin2θ2
The correct Answer is:C
To solve the problem, we need to analyze the motion of a block sliding down two different inclined planes with the same height but different angles. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Problem
We have two inclined planes with angles θ₁ and θ₂, both having the same height (H). A block is released from rest at the top of each incline, and we want to find the relationship between the times taken to slide down each incline, t₁ and t₂.
Step 2: Identify the Forces
When the block is on the incline, the gravitational force acting on it can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline (causing the block to slide down): mgsinθ
Step 3: Determine the Acceleration
The acceleration of the block down each incline can be expressed as:
- For incline 1 (angle θ₁):
a1=gsinθ1
- For incline 2 (angle θ₂):
a2=gsinθ2
Step 4: Relate Height to Length of Incline
Using trigonometry, the length of the incline can be related to the height:
- For incline 1:
L1=Hsinθ1
- For incline 2:
L2=Hsinθ2
Step 5: Use Kinematic Equations
Using the kinematic equation for motion under constant acceleration, where initial velocity u=0:
s=ut+12at2
We can write for both inclines:
- For incline 1:
L1=12gsinθ1t21
- For incline 2:
L2=12gsinθ2t22
Step 6: Substitute Lengths
Substituting the expressions for L1 and L2:
- For incline 1:
Hsinθ1=12gsinθ1t21
- For incline 2:
Hsinθ2=12gsinθ2t22
Step 7: Set Up Ratios
Now, we can set up the ratios of the two equations:
H/sinθ1H/sinθ2=12gsinθ1t2112gsinθ2t22
This simplifies to:
sinθ2sinθ1=sinθ1t21sinθ2t22
Step 8: Solve for Time Ratio
Cross-multiplying gives us:
sin2θ2t21=sin2θ1t22
Taking the square root of both sides, we find:
t1t2=sinθ2sinθ1
Thus, we can express the relationship as:
t2t1=sinθ1sinθ2
Final Result
The relation between t1 and t2 is:
t2t1=sinθ1sinθ2
We have two inclined planes with angles θ₁ and θ₂, both having the same height (H). A block is released from rest at the top of each incline, and we want to find the relationship between the times taken to slide down each incline, t₁ and t₂.
When the block is on the incline, the gravitational force acting on it can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline (causing the block to slide down): mgsinθ
The acceleration of the block down each incline can be expressed as:
- For incline 1 (angle θ₁):
a1=gsinθ1
- For incline 2 (angle θ₂):
a2=gsinθ2
Using trigonometry, the length of the incline can be related to the height:
- For incline 1:
L1=Hsinθ1
- For incline 2:
L2=Hsinθ2
Using the kinematic equation for motion under constant acceleration, where initial velocity u=0:
s=ut+12at2
We can write for both inclines:
- For incline 1:
L1=12gsinθ1t21
- For incline 2:
L2=12gsinθ2t22
Substituting the expressions for L1 and L2:
- For incline 1:
Hsinθ1=12gsinθ1t21
- For incline 2:
Hsinθ2=12gsinθ2t22
Now, we can set up the ratios of the two equations:
H/sinθ1H/sinθ2=12gsinθ1t2112gsinθ2t22
This simplifies to:
sinθ2sinθ1=sinθ1t21sinθ2t22
Cross-multiplying gives us:
sin2θ2t21=sin2θ1t22
Taking the square root of both sides, we find:
t1t2=sinθ2sinθ1
Thus, we can express the relationship as:
t2t1=sinθ1sinθ2
The relation between t1 and t2 is:
t2t1=sinθ1sinθ2
Topper's Solved these Questions
Similar Questions
A block released from rest from the tope of a smooth inclined plane of angle of inclination θ1=30∘ reaches the bottom in time t1. The same block, released from rest from the top of another smooth inclined plane of angle of inclination θ2=45∘ reaches the bottom in time t2. Time t1 and t2 are related as ( Assume that the initial heights of blocks in the two cases are equal ).
View SolutionA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclina-tion is doubled for the same length of the plane, what will be the velocity of the body on reach ing the ground .
View Solution
Knowledge Check
- Question 1 - Select One
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1 - Question 2 - Select One
A block mass 3 kg slides down a frictionless inclined plane of length 6 m and height 4 m. if the block is released from rest at the top of the incline, what is its speed at the bottom?
A5m/sB6m/sC8m/sD9m/s
A body starts rolling down an inclined plane of length L and height h. This body reaches the bottom of the plane in time t. The relation between L and t is?
View SolutionA block is released from the top of a smooth inclined plane of inclination θ as shown in figure. Let υ be the speed of the particle after travelling a distance s down the plane. Then which of the following will remain constant ?
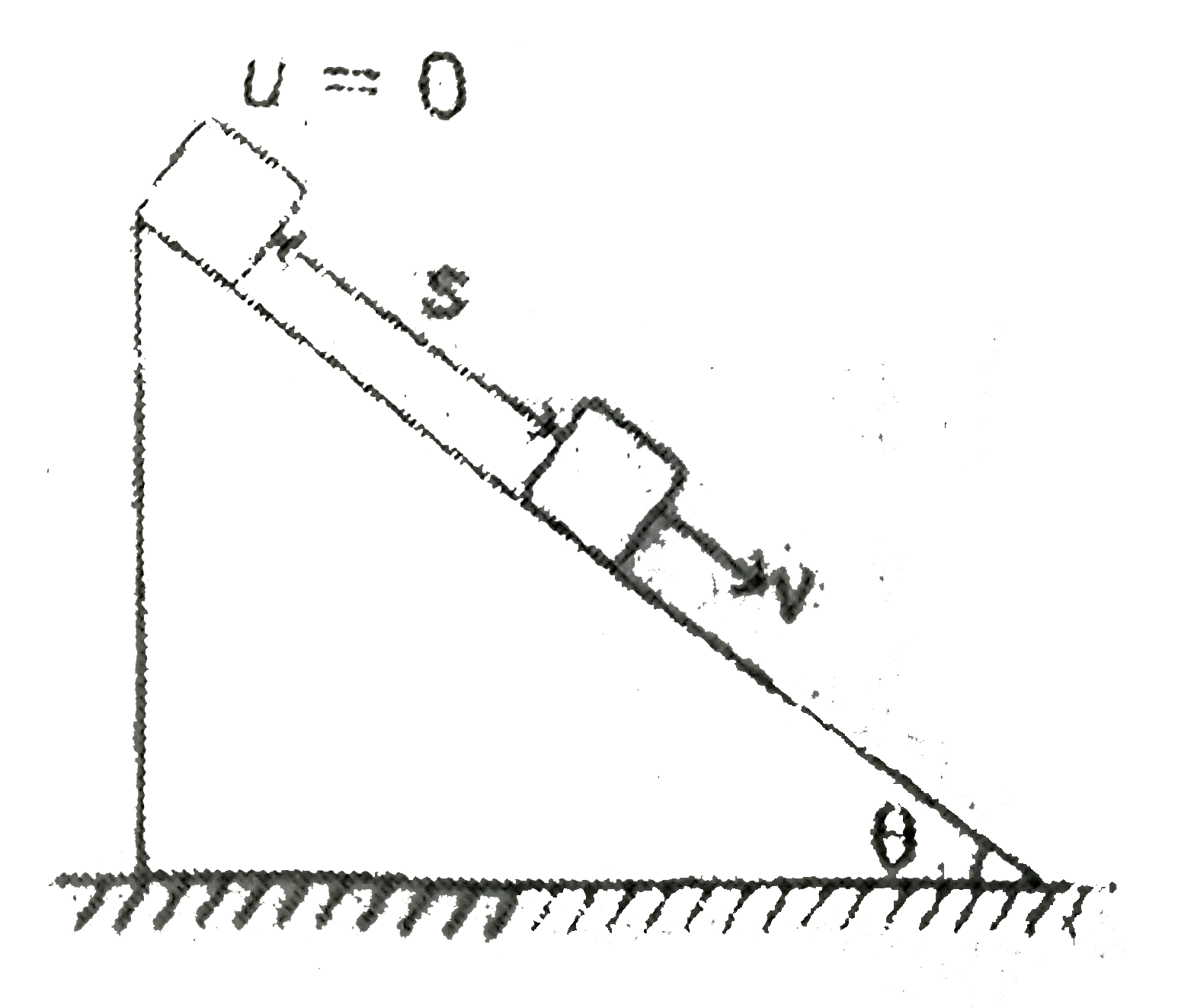 View Solution
View SolutionThe upper half of an inclined plane with an angle of inclination theta, is smooth while the lower half is rough. A body starting from rest at the top of the inclined plane comes to rest at the bottom of the inclined plane. Then the coefficient of friction for the lower half is
View SolutionA uniform disc is released from the top of a rough inclined plane of angle θ and height h. The coefficient of friction between the disc and the plane is μ=tanθ4. The speed of centre of mass of disc on reaching the bottom of the plane is
View SolutionFrom the top of a tower, a stone is thrown up and it reaches the ground in time t1A second stone is thrown down with the same speed and it reaches the ground in time t2 A third stone is released from rest and it reaches the ground in time The correct relation between t1,t2 and t3 is :
View SolutionA triangular prism of mass m placed on it is released from rest on a smooth inclined plane of inclination θ The block does not slip on the prism. Then
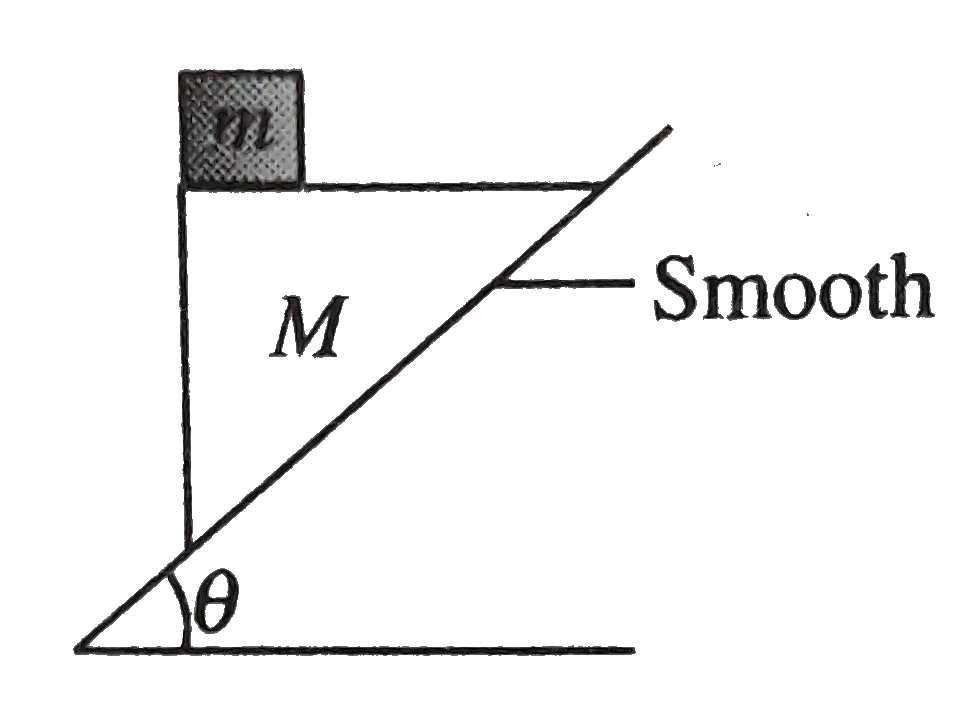 View Solution
View Solution

