A bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω rad/s about the vertical support. About the point of suspension
angular momentum is conserved
angular momentum changes in magnitude but not in direction
angular momentum changes in direction but not in magnitude
angular momentum changes both in direction and magnitude
The correct Answer is:A
Magnitude of radius vector →r=|→r|=l constant.
Magnitude of the momentum →p of the bob
= |→p| = mv = mωl = constant
As angular momentum →L=→r×→p and the angle between →rand→p is always 90∘.
∣∣→L∣∣=l⋅mωl⋅sin90∘=ml2ω = constant
Also, →r is l aways radially outwards and →p is tangential. So →L is always directed along the axis of rotation. So its direction is also fixed.
Topper's Solved these Questions
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXAMINATION ARCHIVE with solutions (AIPMT )
3 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXAMINATION ARCHIVE with solutions (NEET )
8 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXAMINATION ARCHIVE with solutions (WBJEE )
6 Videos
- QUESTION PAPERS OF WBCHSE -2018BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
Similar Questions
A bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View SolutionA bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
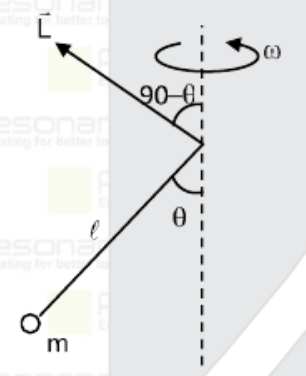
View Solution
Knowledge Check
A bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
Aangular momentum is conserved.Bangular momentum changes in magnitude but not is direction.Cangular momentum changes in direction but not in magnitude.Dangular momentum changes both in direction and magnitude.A smalll bob attached to a string of length l is suspended from a rigid support and rotates with uniform speed along a circle in a horizontal plane. Let θ be the angle made by the string with the vertical, then the length of a simple pendulum having the same period is
Al/cosθBlsinθCl/sinθDlcosθA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
A√glB√3glC√2glD√5gl
A bob of mass m attached to an inextensible string of length l is suspended from a verticle support. The bob rotates in a horizontal circle with an angular speed ωrad/s about the verticle. About the point of suspension.
View SolutionA particle of mass m is attached to a vertical rod with two inextensible strings AO and BO of equal lengths l. Distance between A and B is also l. The setup is rotated with angular speed ω with rod as the axis.
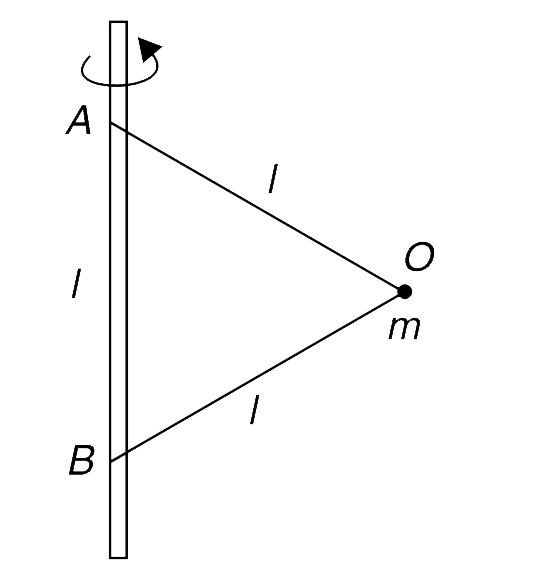
View SolutionA metal bob of mass 0.6 kg is attached to the end of a string of length 1 m and the bob is whirled in a horizontal circle with a uniform speed of 12 m/s. What is the centripetal force acting on the bob ? If the speed of the bob is 5 m/s calculate the tension in the string.
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
View SolutionA pendulum consists of a bob of mass m=0.1kg and a massless inextensible string of length l=1.0m. It is suspended from a fixed point at height h=0.9m above a frictionless horizontal floor. Initially, the bob of the pendulum is lying on the floor at rest vertically below the point of suspension. A horizontal impulse P=02.kg−m/s is imparted to the bob lifts off the floor. The magnitude of the angular momentum of the pendulum about the point of suspension just before the bob lifts off is J kg-m2/s. The kinetic energy of the pendulum just after the lift-off js K Joules.
The value of K is ___
View Solution
