A bob of mass m is projected with a horizontal velocity v=√gl2 as shown in figure. In consequence, it moves in a circular path in a vertical plane by the inextensible string which passes over the smooth fixed peg. Find the maximum angle that the bob swings in the left hand side.
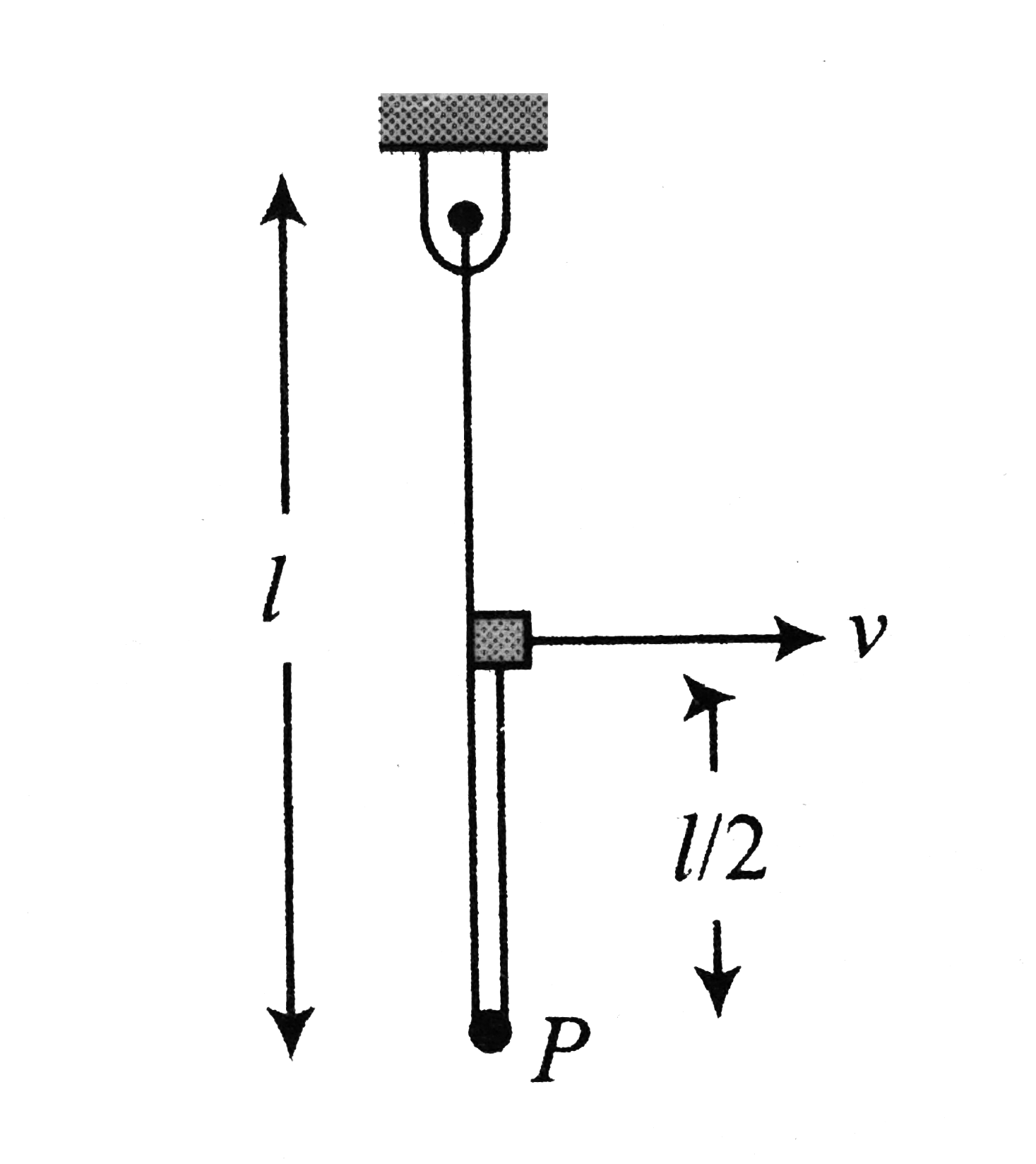
The correct Answer is:cos−1(16)
Apply conservation of energy between A and B.
12mv2+mgl=(mg)3l2[1−cosθ]
v2+2gl=3gl[1−cosθ]
Put v=√gl2
gl2+2gl=3gl[1−cosθ]
52=3[1−cosθ]
⇒56=1−cosθ⇒cosθ=16⇒θ=cos−1(16)

Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
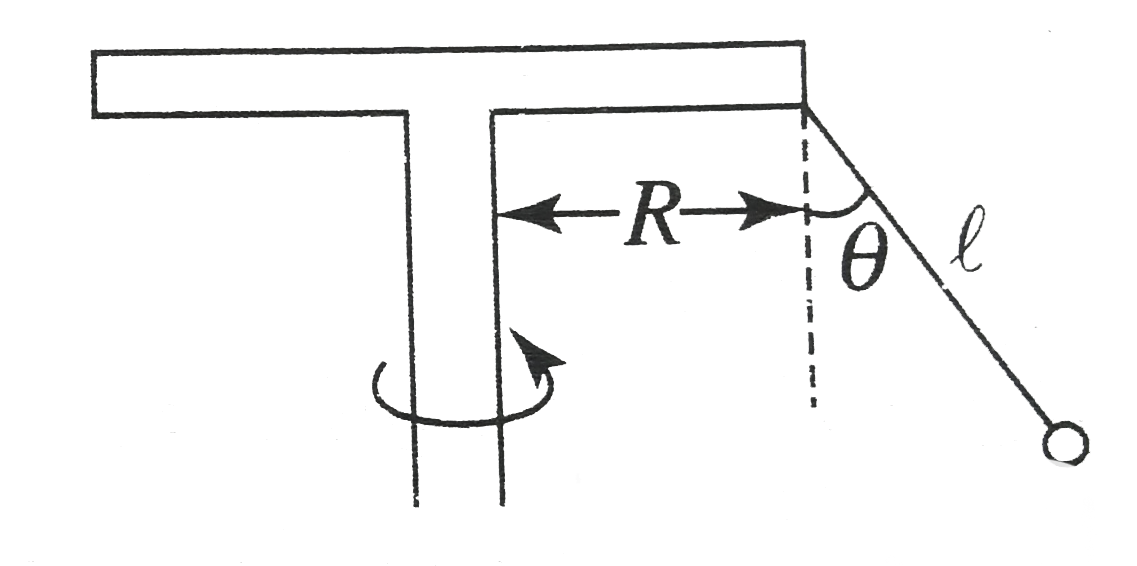
A large mass M and a small mass m hang at two ends of a string that passes over a smooth tube as shown in the figure. The mass m moves around a circular path which lies in a horizontal plane. The length of string from the mass m to the top of the tube is l and θ is the 'angle' this length makes with the vertical. What should be the frequency of rotation of mass m, so that the mass M remains stationary?

View SolutionA particle in projected with velocity √3gL at point A (lowest point of the circle) in the vertical plane. Find the maximum height about horizontal level of point A if the string slacks at the point B as shown in figure.

View Solution
Knowledge Check
A pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. tension in the string
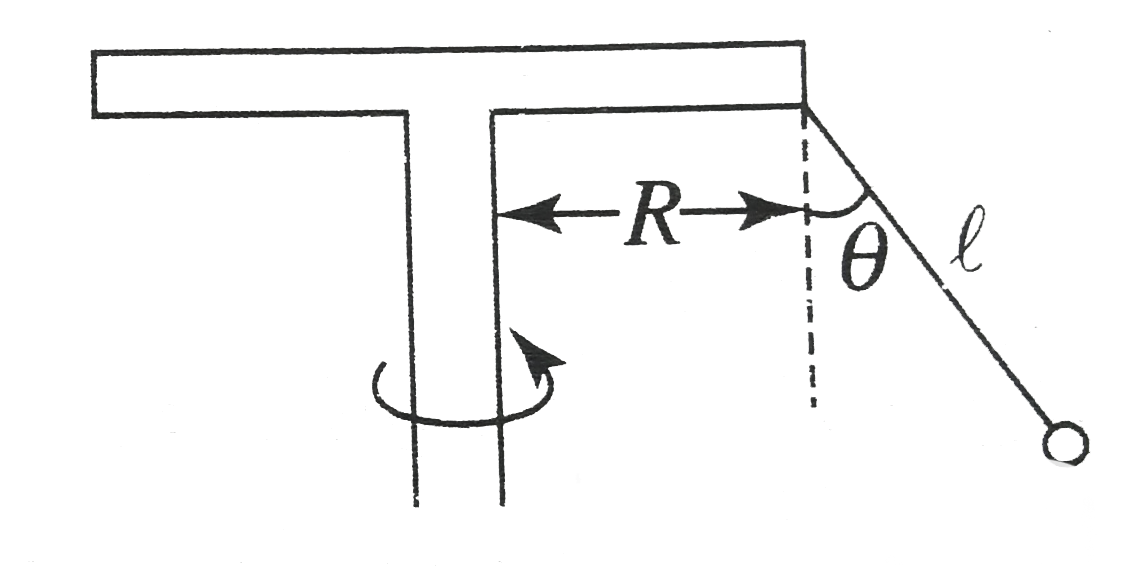 AT=m>anθBT=mgsecθCT=mgsinθcosθDT=mgcotθ
AT=m>anθBT=mgsecθCT=mgsinθcosθDT=mgcotθA conical pendulum consists of a bob of mass m in motion in a circular path in a horizontal plane as shown in figure. During the motion, the supporting wire of length l. Maintains a constant angle θ with the vertical. The magnitude of the angular momentum of the bob about the vertical dashed line is.
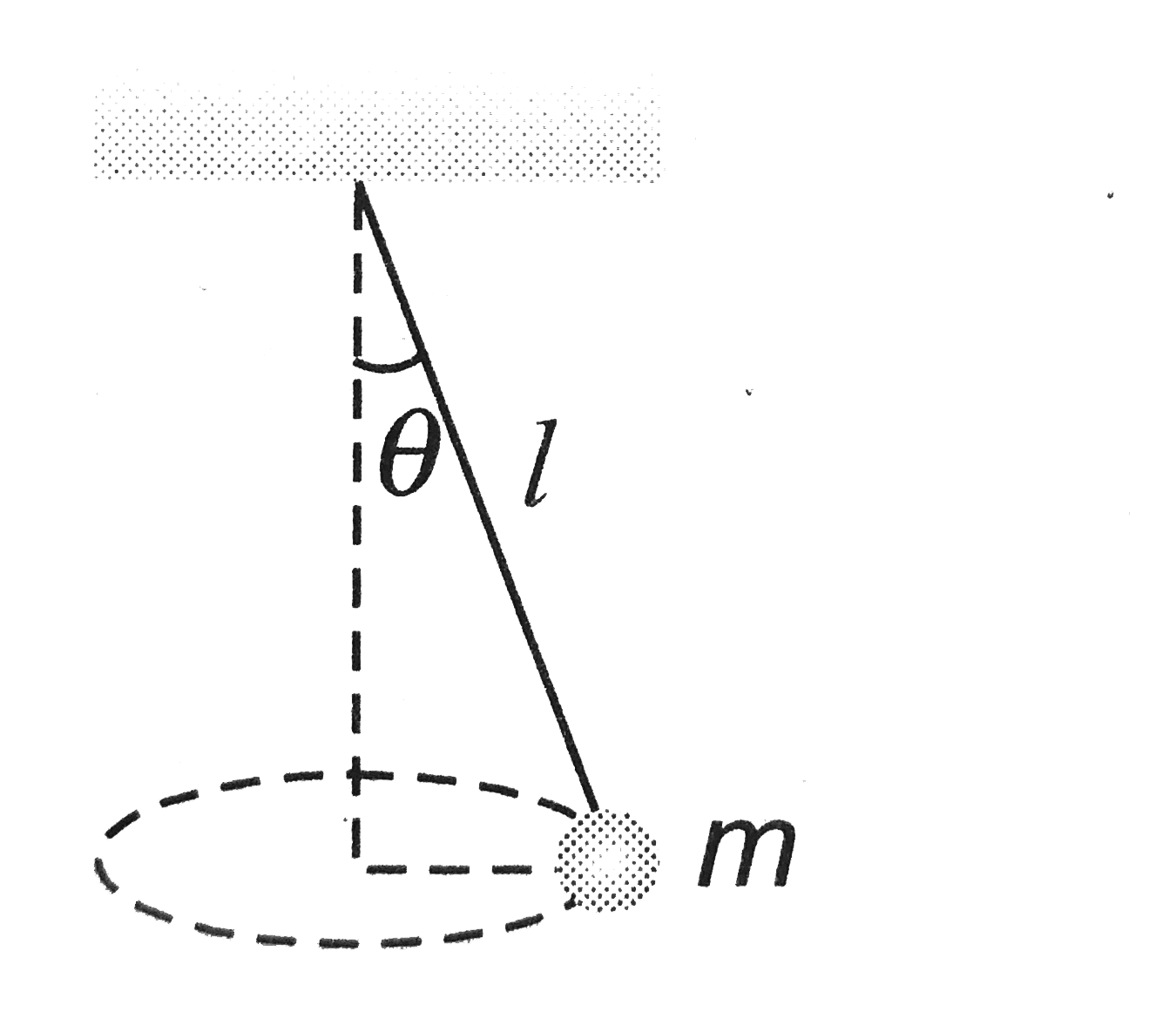 .A(m2gl3cos4θsinθ)1/2B(m2gl3cos4θcosθ)1/2C(m2gl3sin3θcosθ)1/2D(m2gl3cos3θcosθ)1/2.
.A(m2gl3cos4θsinθ)1/2B(m2gl3cos4θcosθ)1/2C(m2gl3sin3θcosθ)1/2D(m2gl3cos3θcosθ)1/2.Two masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
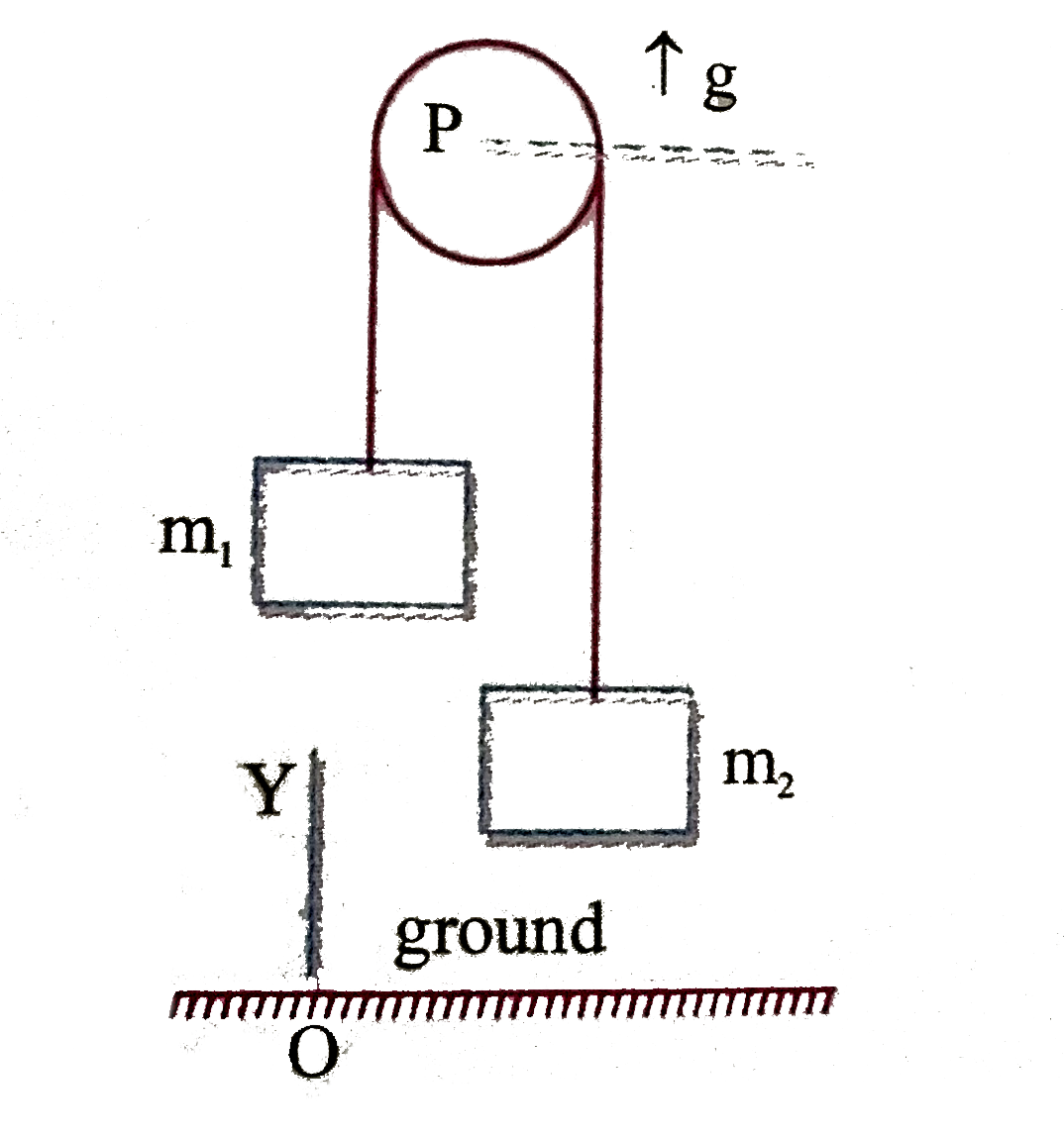 .ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g
.ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g
A simple pendulum of length L having a bob of mass m is deflected from its rest position by an angle θ and released figure. The string hits a peg which is fixed at distance x below the point of suspension and the bob starts going in a circle centred at the peg. a. Assuming that initially the bob has a height less thasn the peg, show that the maximum height reached by the bob equals its initialheight. b. If the pendulum is released with θ=900 and m=L2 find the maximum height reached by the bob above its lowest positon before the string becomes slack. c. Find the minimum value of x/L for which the bob goes in a complete circle about the pet when the pendulum is released from θ=900.
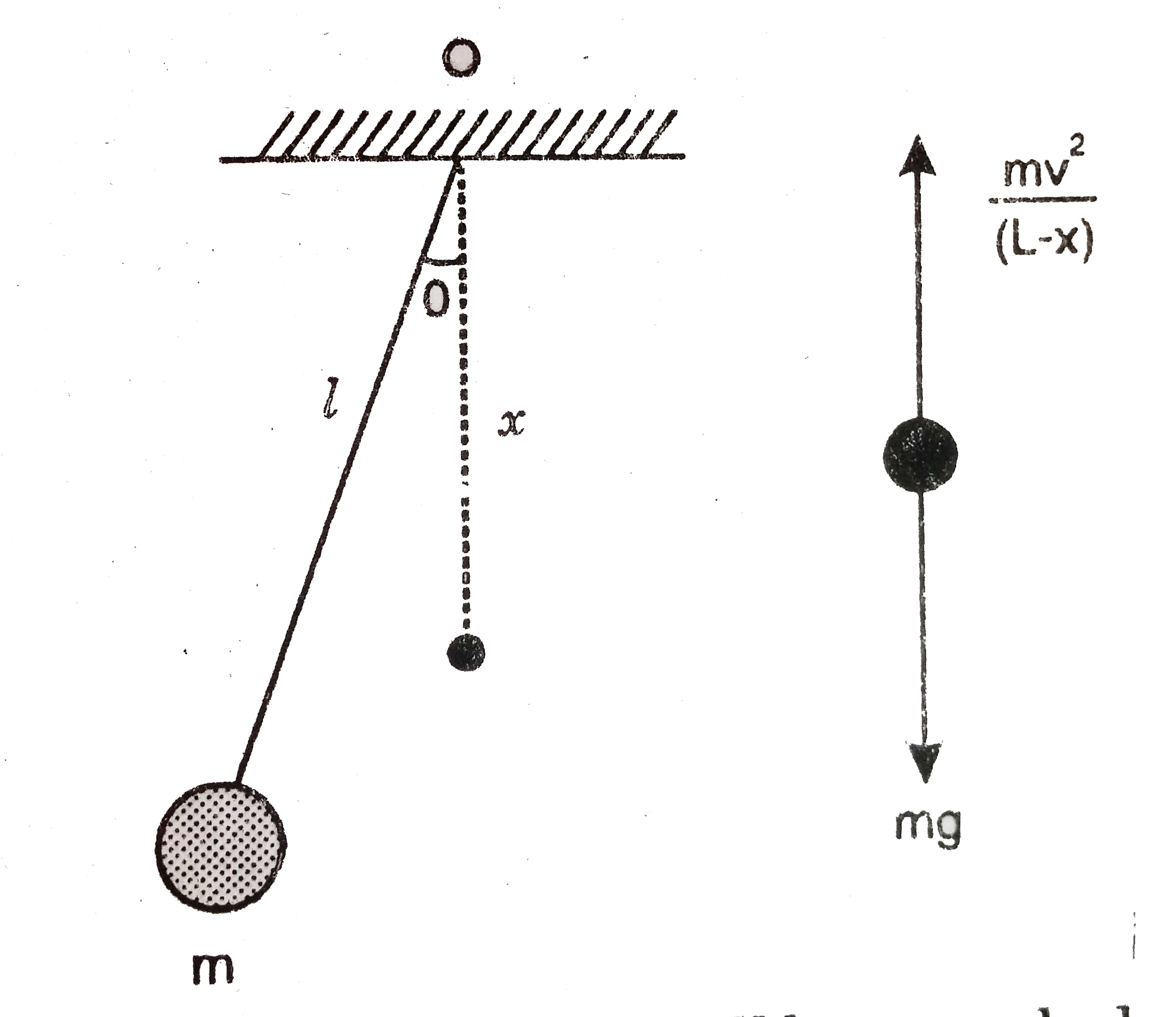
View SolutionA bob of mass m attached with a string of length l tied to a point on ceiling is released from a position when its string is horizontal. At the bottom most point of its motion, an identical mass m gently stuck to it. Find the maximum angle from the vertical to which it rotates.
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. angular speed ω
View SolutionA simple pendulum of length L swings in a vertical plane. The tension of the string when it makes an angle θ with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
View SolutionA bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elasticallywith another bob of mass 2m suspended by a string of length l2, which is initially at rest. Both strings are massless and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l2/l1 is (5/4)n. The value of n is
View Solution
