A bob of mass 'm' suspended by a thread of length I undergoes simple harmonic osillations with time peroid T. If the bob is immersed in a liquiod tha has density 14 times that of the bob and the length of the thread is increased by 1/3rd of the original length ,then the time period of the simple harmonic oscilltions will be :
T
32T
43T
34T
To solve the problem, we need to determine the new time period of the simple harmonic oscillations of a bob when it is immersed in a liquid and the length of the thread is increased.
1. Initial Time Period Calculation:
The time period T of a simple pendulum is given by the formula:
T=2π√lg
where l is the length of the pendulum and g is the acceleration due to gravity.
2. New Length Calculation:
The length of the thread is increased by 13 of the original length l. Therefore, the new length l′ is:
l′=l+l3=4l3
3. Effective Gravity Calculation:
When the bob is immersed in a liquid with a density that is 14 times that of the bob, we need to find the effective acceleration due to gravity g′. The effective weight of the bob in the liquid is reduced due to buoyancy. The buoyant force Fb can be calculated using Archimedes' principle:
Fb=V⋅ρliquid⋅g
where V is the volume of the bob and ρliquid=ρbob4.
The volume V of the bob can be expressed as:
V=mρbob
Therefore, the buoyant force becomes:
Fb=mρbob⋅(ρbob4)⋅g=mg4
The effective weight W′ of the bob in the liquid is:
W′=mg−Fb=mg−mg4=3mg4
The effective acceleration due to gravity g′ can be calculated as:
W′=mg′⇒g′=3g4
4. New Time Period Calculation:
Now we can substitute the new length l′ and the effective gravity g′ into the time period formula:
T′=2π√l′g′=2π
⎷4l33g4
Simplifying this gives:
T′=2π√4l⋅43⋅3g=2π√16l9g=4π3√lg
5. Final Expression:
Since the original time period T=2π√lg, we can express the new time period T′ in terms of T:
T′=43T
Conclusion:
The new time period of the simple harmonic oscillations when the bob is immersed in the liquid and the length of the thread is increased is:
T′=43T
The time period T of a simple pendulum is given by the formula:
T=2π√lg
where l is the length of the pendulum and g is the acceleration due to gravity.
The length of the thread is increased by 13 of the original length l. Therefore, the new length l′ is:
l′=l+l3=4l3
When the bob is immersed in a liquid with a density that is 14 times that of the bob, we need to find the effective acceleration due to gravity g′. The effective weight of the bob in the liquid is reduced due to buoyancy. The buoyant force Fb can be calculated using Archimedes' principle:
Fb=V⋅ρliquid⋅g
where V is the volume of the bob and ρliquid=ρbob4.
V=mρbob
Therefore, the buoyant force becomes:
Fb=mρbob⋅(ρbob4)⋅g=mg4
W′=mg−Fb=mg−mg4=3mg4
W′=mg′⇒g′=3g4
Now we can substitute the new length l′ and the effective gravity g′ into the time period formula:
T′=2π√l′g′=2π
⎷4l33g4
Simplifying this gives:
T′=2π√4l⋅43⋅3g=2π√16l9g=4π3√lg
Since the original time period T=2π√lg, we can express the new time period T′ in terms of T:
T′=43T
The new time period of the simple harmonic oscillations when the bob is immersed in the liquid and the length of the thread is increased is:
T′=43T
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics Section B20videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section A)81videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS30videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS246videos
JEE MAINS 2020
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)10videos
JEE MAINS 2022
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle undergoes simple harmonic motion having time period T. The time taken in 3/8th oscillation is
A38TB58TC512TD712T - Question 2 - Select One
A simple pendulum has a time period T in vacuum. Its time period when it is completely immersed in a liquid of density one-eight of the density of material of the bob is
A√87TB√58TC√32TD√38T - Question 3 - Select One
Simple pendulum is executing simple harmonic motion with time period T. If the length of the pendulum is increased by 21%, then the increase in the time period of the pendulum of the increased length is:
A22%B13%C50%D10%
A pendulum having length L has time period T0 in air. When it is dipped in water having density 14th of density of bob. Length of pendulum is increased to 34 times initial length. Then new time period T' is
View SolutionThe time period of a simple pendulum is 5 seconds. If mass of the bob is increased to 4 times the original, the new time period of it is ____
View SolutionA simple pendulum is executing simple harmonic motion with a time period T. If the length of the pendulum is increased by 21%, the percentage increase in the time period of the pendulum of is
View SolutionA simple pendulum of length l0 can perform simple harmonic oscillations with a time period T0. If the length of the pendulum is decreased to l016 then the time time period of oscillation will become.
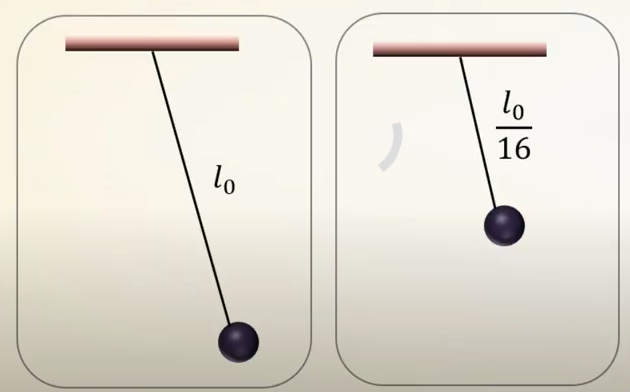 View Solution
View SolutionA simple pendulum oscillating in air has a time period of √3s. Now the bob of the pendulum is completely immersed in a non-viscous liquid whose density is equal to 14th that of the material of the bob. The new time period of simple pendulum will be
View Solution

