A body is projected from the bottom of a smooth inclined place with a velocity of 20ms−1, If it is just sufficient to carry it to the top in 4s, find the inclination and height of the plane.
To solve the problem of a body projected from the bottom of a smooth inclined plane with an initial velocity of 20m/s and reaching the top in 4s, we can follow these steps:
Step 1: Identify the given parameters
- Initial velocity, u=20m/s
- Time of travel, t=4s
- Final velocity at the top of the incline, v=0m/s (since it just reaches the top and momentarily stops)
Step 2: Apply the first equation of motion
The first equation of motion relates initial velocity, final velocity, acceleration, and time:
v=u+at
Here, a is the acceleration (which will be negative since the body is decelerating due to gravity). The acceleration along the incline can be expressed as:
a=−gsinθ
Substituting the known values into the equation:
0=20−gsinθ⋅4
Rearranging gives:
gsinθ=204=5m/s2
Step 3: Solve for sinθ
Using g≈10m/s2, we can find sinθ:
sinθ=510=12
From this, we can determine the angle θ:
θ=30∘
Step 4: Calculate the height of the incline
To find the height h reached by the body, we can use the third equation of motion:
s=ut+12at2
Here, s is the distance along the incline, which can be expressed in terms of height h and angle θ:
s=hsinθ
Substituting a=−gsinθ into the equation gives:
h=(20⋅4)+12(−gsinθ)⋅(42)
Substituting sinθ=12 and g=10m/s2:
h=80−12⋅10⋅12⋅16
Calculating the second term:
h=80−20=60m
Final Results
- The angle of inclination θ=30∘
- The height of the incline h=60m
- Initial velocity, u=20m/s
- Time of travel, t=4s
- Final velocity at the top of the incline, v=0m/s (since it just reaches the top and momentarily stops)
The first equation of motion relates initial velocity, final velocity, acceleration, and time:
v=u+at
Here, a is the acceleration (which will be negative since the body is decelerating due to gravity). The acceleration along the incline can be expressed as:
a=−gsinθ
Substituting the known values into the equation:
0=20−gsinθ⋅4
Rearranging gives:
gsinθ=204=5m/s2
Using g≈10m/s2, we can find sinθ:
sinθ=510=12
From this, we can determine the angle θ:
θ=30∘
To find the height h reached by the body, we can use the third equation of motion:
s=ut+12at2
Here, s is the distance along the incline, which can be expressed in terms of height h and angle θ:
s=hsinθ
Substituting a=−gsinθ into the equation gives:
h=(20⋅4)+12(−gsinθ)⋅(42)
Substituting sinθ=12 and g=10m/s2:
h=80−12⋅10⋅12⋅16
Calculating the second term:
h=80−20=60m
- The angle of inclination θ=30∘
- The height of the incline h=60m
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.3
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.4
16 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View SolutionA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclina-tion is doubled for the same length of the plane, what will be the velocity of the body on reach ing the ground .
View SolutionA body is kept on a smooth inclined plane having an inclination of 1 in x. Then,
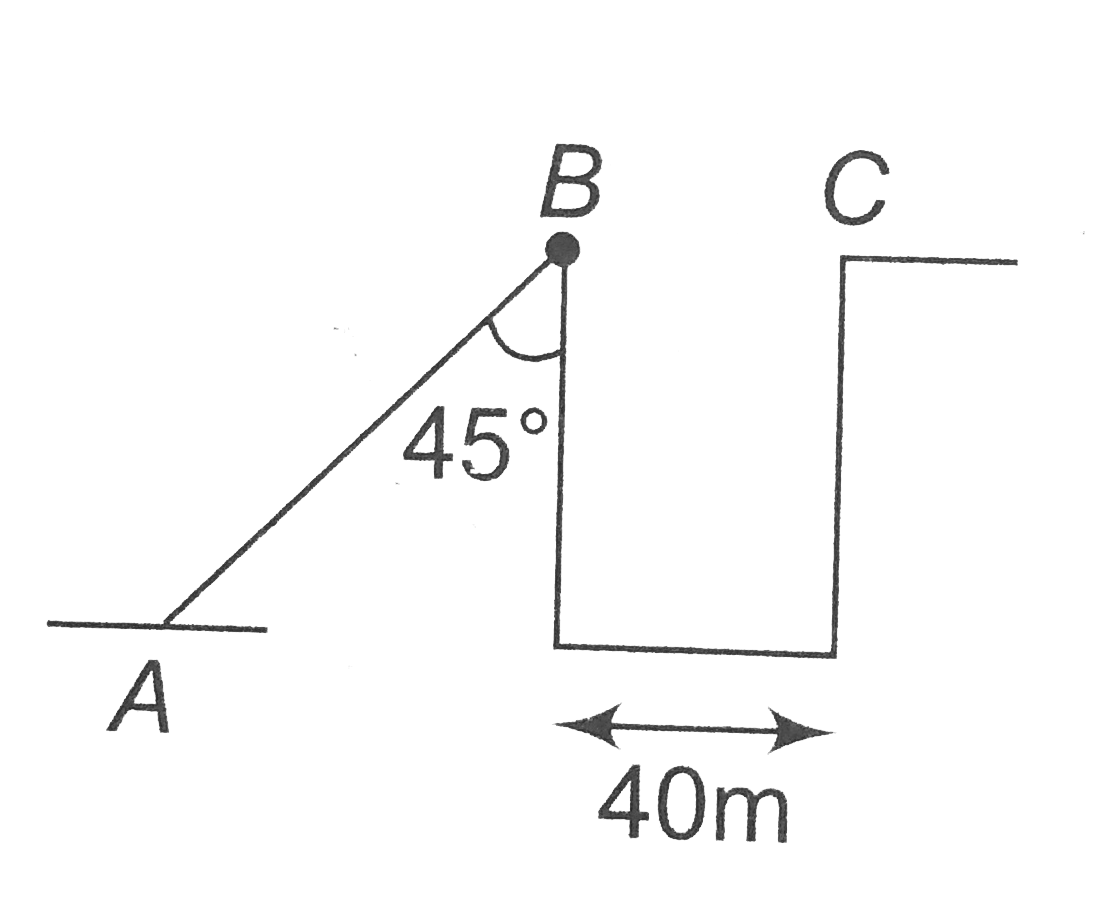
View SolutionA body is projected up a smooth inclined plane with velocity V from the point A as shown in the figure. The angle of inclination is 45∘ and the top is connected to a well of diameter 40m. If the body just manages to across the well, what is the value of V? Length of inclined plane is 20√2m.
View SolutionA body is projected horizontally from the top of a tower with a velocity of 30 m/s. The velocity of the body 4 seconds after projection is (g = 10ms−2)
View Solution
A particle of mass m is projected up from the bottom of an inclined plane with initial velocity v0 at angle 45∘ with an inclined plane of inclination 30∘ as shown in figure. At the same time a small block of same mass m is released from rest at a height h, the particle hits the block at some point on the inclined plane. Neglect friction at inclined.
Q. The value of height h is
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA spherical object of mass m and radius R is released from the top of a smooth inclined plane of height h and angle of inclination is 37° . The radius of gyration of the object is K. The speed of object at the bottom of inclined plane is
View SolutionA bullet is fired from the bottom of the inclined plane at angle θ=37∘ with the inclined plane. The angle of incline is 30∘ with the horizontal. Find the
(a) position of the maximum height of the bullet from the inclined plane ,
(b) time of light ,
( c) range along the incline ,
(d) the value of θ at which the range will be maximum ,
( e) maximum range.
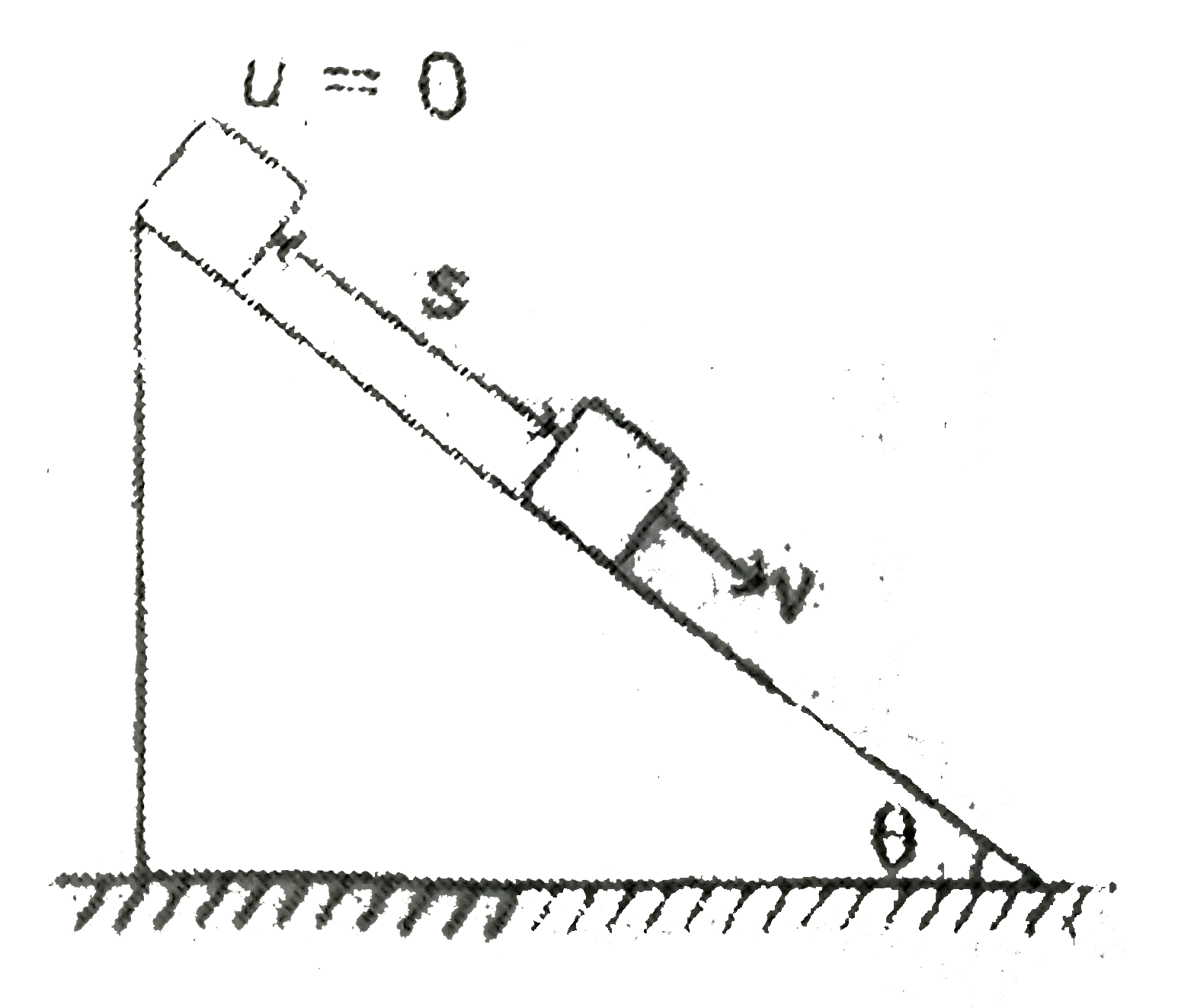
View SolutionA block is released from the top of a smooth inclined plane of inclination θ as shown in figure. Let υ be the speed of the particle after travelling a distance s down the plane. Then which of the following will remain constant ?
View Solution
