A body of mass $5 \times 10^{- 3}$ kg is launched upon a rough inclined plane making an angle of $30^{\circ}$ with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.

Video Solution

Text Solution

Verified by Experts

Here, $m = 5 \times 10^{- 3} k g, θ = 30^{\circ}, μ = ? T_{1} = \frac{1}{2} t 2$
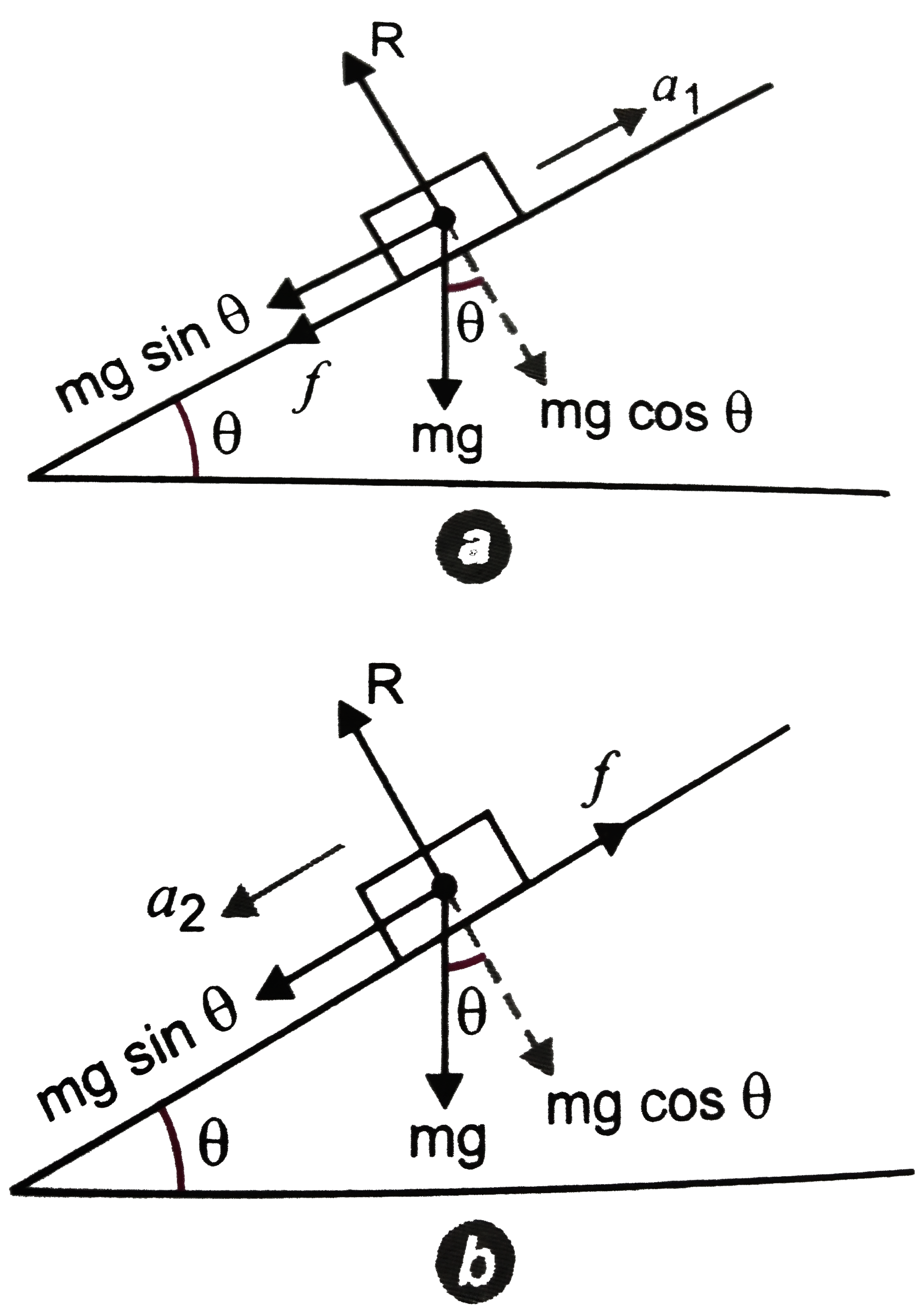
If f is the force of friction between the body and inclined plane , then
$f = μ R = μ m g cos θ$
Let $a_{1}$ be the acceleration while ascending the plane as shown in Here friction is acting down the incline .
$m g sin θ + f = m a_{2}$
let $a_{2}$ be acceleration while descending down the plane as shown in Here , friction is up the plane
$m g sin θ - f = m a_{2}$
Divide (ii) by (iii) $\frac{m g sin θ + f}{m g sin θ - f} = \frac{a_{1}}{a_{2}}$
$\frac{m g sin θ + μ m g cos θ}{m g sin θ - μ m g cos θ} = \frac{a_{1}}{a_{2}}$
$\frac{m g cos θ (tan θ + μ)}{m g cos θ (tan θ - μ)} = \frac{a_{1}}{a_{2}}$
If $t_{1}$ is time of ascent and $t_{2}$ is time of descent for length of plane $(l)$ then
$l = \frac{1}{2} a_{1} t_{1}^{2} = \frac{1}{2} a_{2} t_{2}^{2}$
$\frac{a_{1}}{a_{2}} = \frac{t_{2}^{2}}{t_{1}^{2}} = {(\frac{1}{2})}^{2} = \frac{4}{1}$
From (iv) , $\frac{tan θ + μ}{tan θ - μ} = \frac{4}{1}$
$tan θ + μ = 4 tan θ - 4 μ$
$5 μ = 3 tan θ$
$μ = \frac{3}{5} {tan 30}^{\circ} = \frac{3}{\sqrt{3}}$
$μ = \frac{1.732}{5} = 0.346$
.

Updated on:21/07/2023