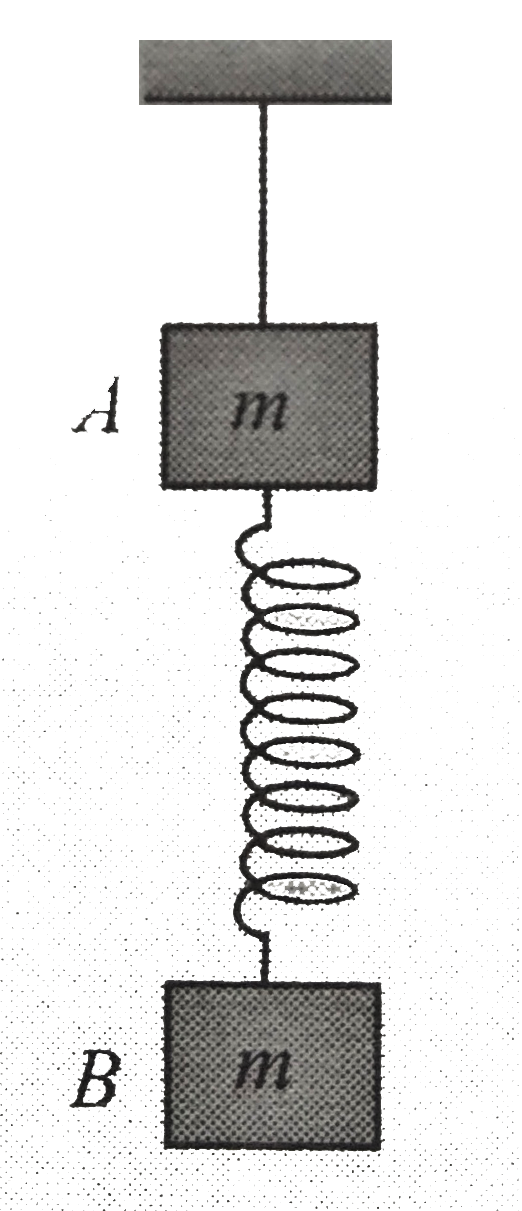A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
The largest amplitude Amax, for which the string will remain taut throughout the motion is
mg2k
mgk
2mg3k
L
The correct Answer is:B
In the position of equilibrium when the tension in the string =mg the extension in the spring is x0=mgk. If the amplitude exceeds this value, then in its upward motion, the body will rise to a height at which the string will become loose and T=0 Hence maximum amplitude is xm=mgk.
It also follows from the fact that for T≥0 the maximum downwards acceleration that the body can have is g. Since f(t)=g−T(t)m, f(t)≤g. Hence maximum amplitude is Am=gω2=mgk
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer
10 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Knowledge Check
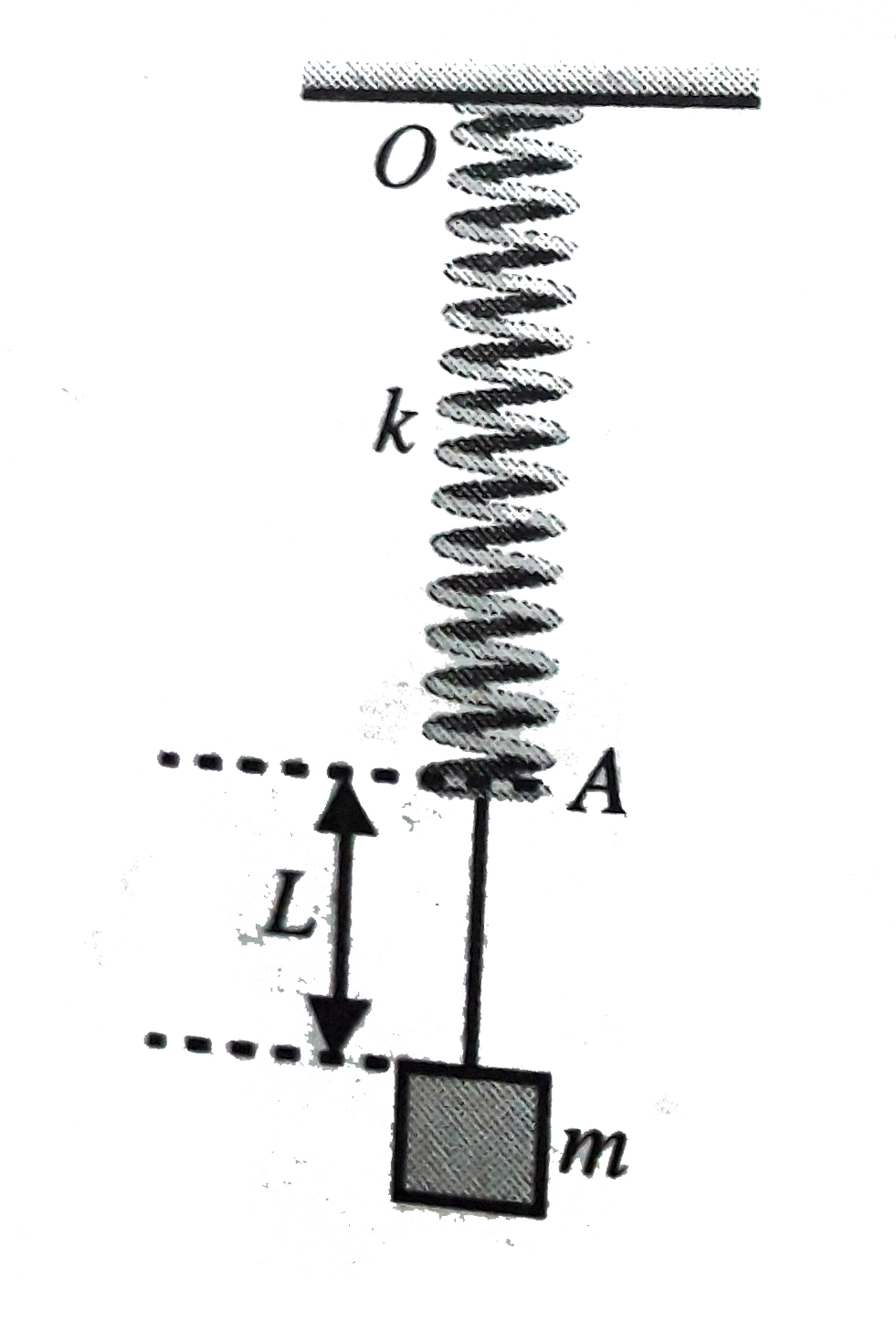
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
Q. If the mass m is now raised up to point A (the top end of the string see fig. and allowed to fall from rest, the maximum extension of the spring in the subsequent motion will beALBmgkCmgk√1+2kLmgDmgk[1+√1+2kLmg]A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
If the mass m, from the initial position of rest is pulled down a distance A and then released, assuming that the string remains taut throughout the motion, the maximum (downwards) acceleration of the oscillating body will beAkAmBkA2mCg2DgFor a body of mass m attached to the spring the spring factor is given by
Am/ω2Bmω2Cm2ωDm2ω2
Two blocks A and B of same mass m attached with a light string are suspended by a spring as shown in fig. Find the acceleration of block A and B just after the string is cut.

View SolutionThe string, the spring and the pulley shown in figure are light. Find the time period of the mass m.

View SolutionA stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v . If the string is released, the stone flies
View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
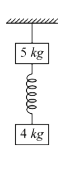
View SolutionTwo block of mass 4 kg and 5 kg attached a light spring are suspended by a string as shown in figure. Find acceleration of block 5 kg and 4 kg just after the string is cut.
View Solution