Question

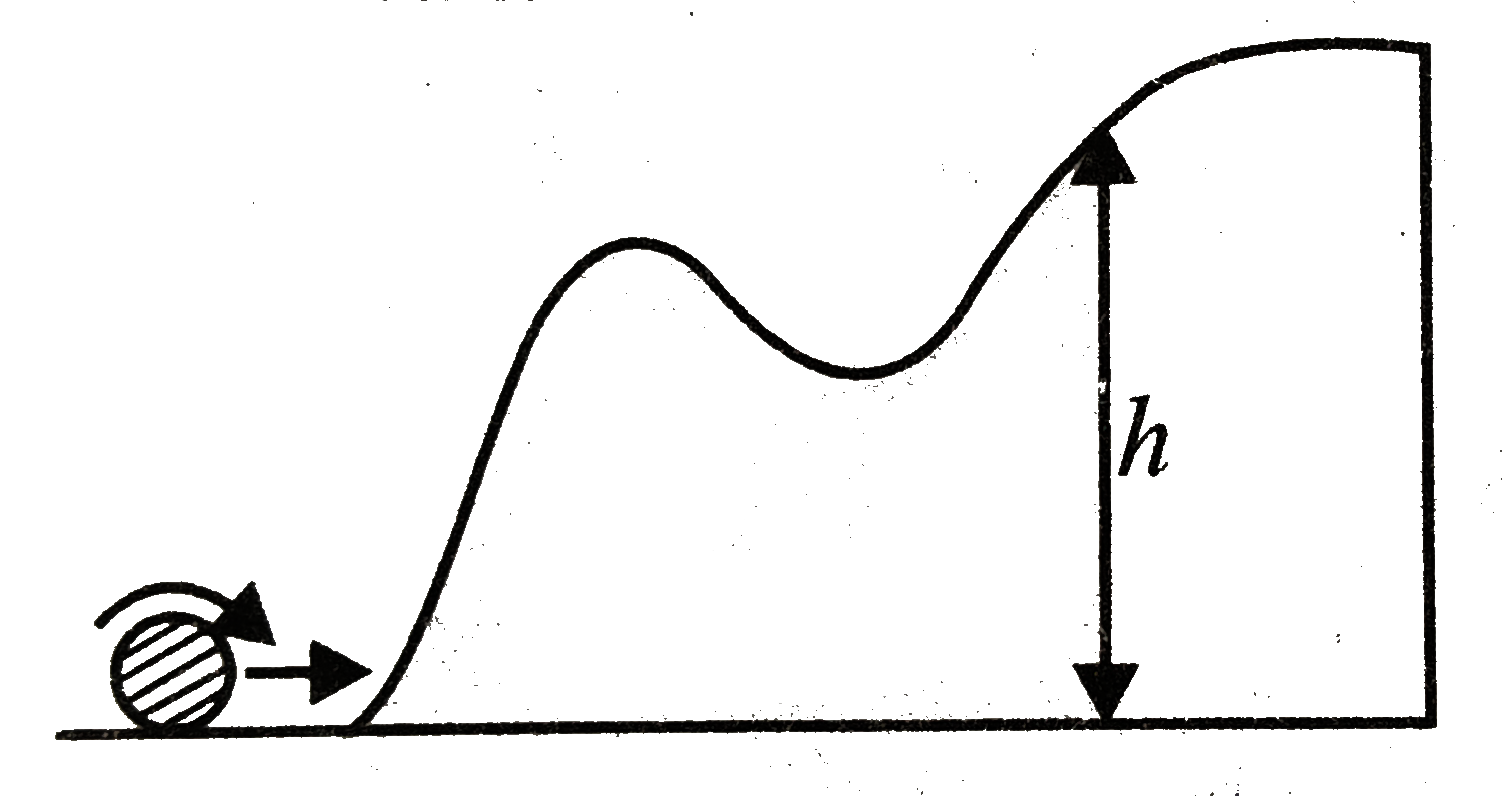
A body of radius $R$ and mass $m$ is rolling smoothly with speed $v$ on a horizontal surface. It then rolls up a hill to a maximum height $h$. If $h=3v^2/4g$. What might the body be ?

Options

A. solid sphere
B. hollow sphere
C. disc
D. ring

Answer

C

Explanation

To solve the problem, we will use the principle of conservation of energy. The kinetic energy of the rolling body will be converted into potential energy as it rolls up the hill.

1. Identify the given information:
- Mass of the body = \( m \)
- Radius of the body = \( R \)
- Initial speed of the body = \( v \)
- Maximum height reached = \( h = \frac{3v^2}{4g} \)

2. Calculate the potential energy at maximum height:
The potential energy (PE) when the body reaches height \( h \) is given by:
\( PE = mgh = mg \left(\frac{3v^2}{4g}\right) = \frac{3mv^2}{4} \)

3. Calculate the initial kinetic energy:
The total kinetic energy (KE) of the rolling body consists of translational and rotational kinetic energy. The translational kinetic energy is:
\( KE_{trans} = \frac{1}{2} mv^2 \)
The rotational kinetic energy is given by:
\( KE_{rot} = \frac{1}{2} I \omega^2 \)
where \( I \) is the moment of inertia and \( \omega \) is the angular velocity. Since the body is rolling without slipping, we have:
\( \omega = \frac{v}{R} \)
Therefore, substituting \( \omega \):
\( KE_{rot} = \frac{1}{2} I \left(\frac{v}{R}\right)^2 = \frac{1}{2} \frac{I v^2}{R^2} \)

4. Using conservation of energy:
The total initial kinetic energy equals the potential energy at the maximum height:
\( KE_{trans} + KE_{rot} = PE \)
Substituting the expressions we have:
\( \frac{1}{2} mv^2 + \frac{1}{2} \frac{I v^2}{R^2} = \frac{3mv^2}{4} \)

5. Rearranging the equation:
Factor out \( \frac{v^2}{2} \):
\( \frac{v^2}{2} \left(m + \frac{I}{R^2}\right) = \frac{3mv^2}{4} \)
Dividing both sides by \( v^2 \) (assuming \( v \neq 0 \)):
\( \frac{1}{2} \left(m + \frac{I}{R^2}\right) = \frac{3m}{4} \)

6. Solving for the moment of inertia \( I \):
Multiply both sides by 2:
\( m + \frac{I}{R^2} = \frac{3m}{2} \)
Rearranging gives:
\( \frac{I}{R^2} = \frac{3m}{2} - m = \frac{m}{2} \)
Therefore,
\( I = \frac{mR^2}{2} \)

7. Identifying the body:
The moment of inertia \( I = \frac{mR^2}{2} \) is characteristic of a solid disc. Thus, the body is a disc.

Final Answer:
The body might be a disc.