A boy of mass 60kg is standing over a platform of mass 40kg placed over a smooth horizontal surface. He throws a stone of mass 1kg with velocity v=10m/s at an angle of 45∘ with respect to the ground. Find the displacement of the platform (with boy) on the horizontal surface when the stone lands on the ground. Take g=10m/s2.
25 cm
5 cm
10 cm
50 cm
To solve the problem step by step, we will follow these steps:
Step 1: Analyze the motion of the stone
The boy throws a stone of mass ms=1kg with a velocity v=10m/s at an angle θ=45∘. We need to find the horizontal range of the stone.
Hint: Use the formula for the range of projectile motion:
R=v2sin(2θ)g
Step 2: Calculate the range of the stone
Substituting the values into the range formula:
R=(10m/s)2⋅sin(90∘)10m/s2
Since sin(90∘)=1:
R=10010=10m
Hint: The stone will land 10 meters away horizontally from the point of projection.
Step 3: Determine the initial momentum of the system
Before the stone is thrown, the total momentum of the system (boy + platform) is zero since they are at rest.
Hint: The momentum of the system must remain conserved.
Step 4: Calculate the momentum after the stone is thrown
When the boy throws the stone, he will experience an equal and opposite reaction (according to Newton's third law). The momentum of the stone is:
ps=ms⋅v=1kg⋅10m/s=10kg m/s
The total mass of the boy and platform is mb+mp=60kg+40kg=100kg.
Hint: The platform (with the boy) will move in the opposite direction to conserve momentum.
Step 5: Calculate the velocity of the platform and boy
Let vp be the velocity of the platform and boy after the stone is thrown. Using conservation of momentum:
0=ms⋅v+(mb+mp)⋅vp
0=10+100⋅vp
Solving for vp:
100vp=−10⟹vp=−10100=−0.1m/s
Hint: The negative sign indicates that the platform moves in the opposite direction to the stone.
Step 6: Calculate the time of flight of the stone
The time of flight t for a projectile is given by:
t=2vsin(θ)g
Substituting the values:
t=2⋅10⋅sin(45∘)10=20⋅√2210=√2s
Hint: The time of flight depends on the vertical component of the initial velocity.
Step 7: Calculate the displacement of the platform
The displacement sp of the platform while the stone is in the air can be calculated using:
sp=vp⋅t
Substituting the values:
sp=−0.1⋅√2≈−0.1414m
Hint: The displacement is negative, indicating movement in the opposite direction.
Step 8: Convert displacement to centimeters
To express the displacement in centimeters:
sp≈−14.14cm
Hint: The magnitude of displacement is what we are interested in.
Final Answer
The displacement of the platform (with the boy) on the horizontal surface when the stone lands on the ground is approximately 14.14cm.
The boy throws a stone of mass ms=1kg with a velocity v=10m/s at an angle θ=45∘. We need to find the horizontal range of the stone.
R=v2sin(2θ)g
Substituting the values into the range formula:
R=(10m/s)2⋅sin(90∘)10m/s2
Since sin(90∘)=1:
R=10010=10m
Before the stone is thrown, the total momentum of the system (boy + platform) is zero since they are at rest.
When the boy throws the stone, he will experience an equal and opposite reaction (according to Newton's third law). The momentum of the stone is:
ps=ms⋅v=1kg⋅10m/s=10kg m/s
The total mass of the boy and platform is mb+mp=60kg+40kg=100kg.
Let vp be the velocity of the platform and boy after the stone is thrown. Using conservation of momentum:
0=ms⋅v+(mb+mp)⋅vp
0=10+100⋅vp
Solving for vp:
100vp=−10⟹vp=−10100=−0.1m/s
The time of flight t for a projectile is given by:
t=2vsin(θ)g
Substituting the values:
t=2⋅10⋅sin(45∘)10=20⋅√2210=√2s
The displacement sp of the platform while the stone is in the air can be calculated using:
sp=vp⋅t
Substituting the values:
sp=−0.1⋅√2≈−0.1414m
To express the displacement in centimeters:
sp≈−14.14cm
The displacement of the platform (with the boy) on the horizontal surface when the stone lands on the ground is approximately 14.14cm.
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Only one option is correct for JEE Advanced
60 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View SolutionA balloon is moving upwards with velocity 10m/s. It releases a stone which comes down to the ground in 11s. The height of the balloon from the ground at the moment when the stone was dropped is (g=10m/s2)
View SolutionA boy throws a ball with a velocity of 15 m/s at an angle of 15° with the horizontal. The distance at which the ball strikes the ground is
View SolutionTwo men to masses 80kg and 60kg are standing on a wood plank of mass 100kg, that has been placed over a smooth surface. If both the men start moving towards each other with speeds 1m/s and 2m/s respectively then find the velocity of the plank by which it starts moving.
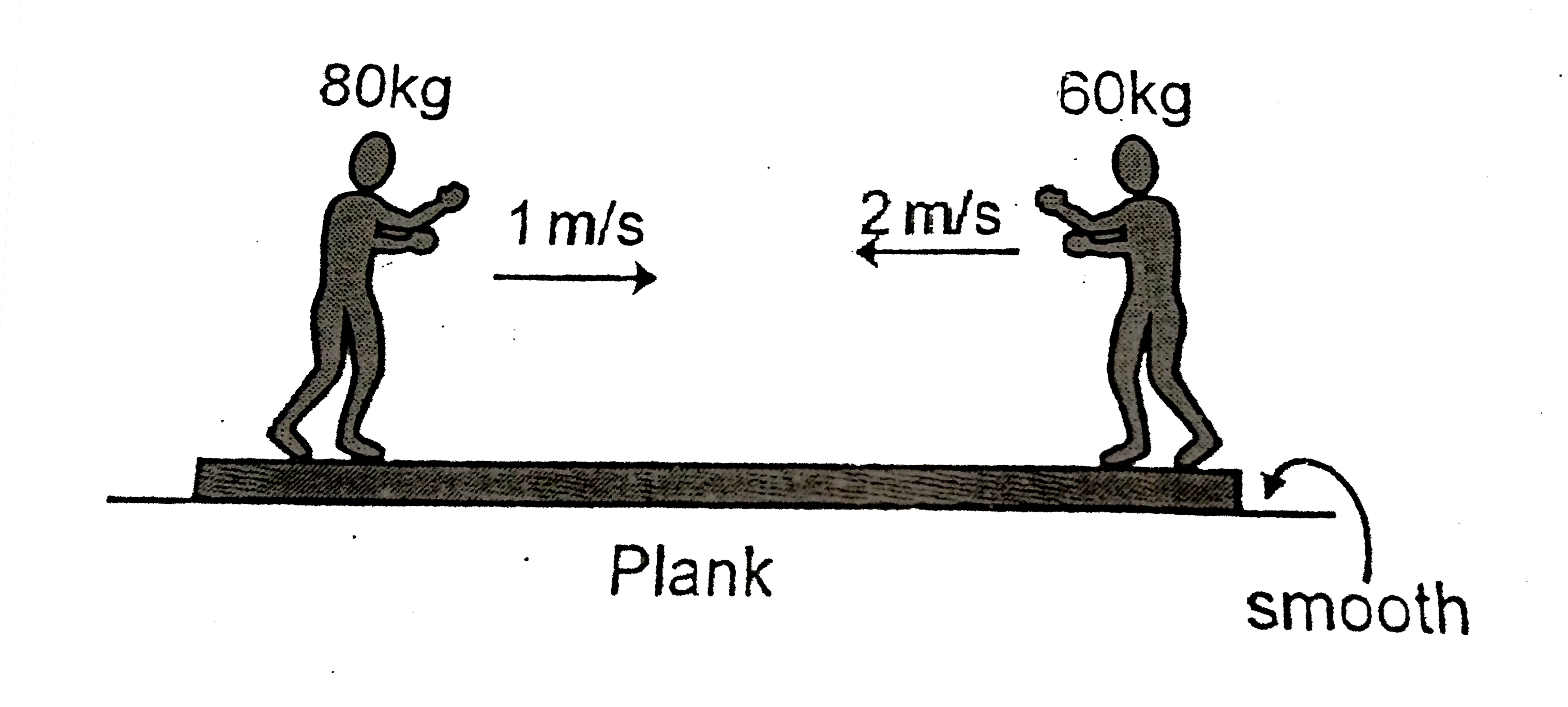
View SolutionA boy throws a stone with a speed of V0=10 m/sec at an angle of θ0=30∘ to the horizontal Find the position of the stone wrt the point of projection just after a time t = 1/2 sec.
View SolutionA block A of mass 2 kg rests on a horizontal surface. Another block B of mass 1 kg moving at a speed of m/s when at a distance of 16 cm from A. collides elastically with A. The coefficeint of friction between the horizontal surface and earth of the blocks is 0.2. Then (g=10m/s2)
View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View SolutionA particle of mass 1kg has been thrown with initial speed 20 ms making an angle 60° with the horizontal ground. the angular momentum of the particle about point of projection when the projectile is at highest point is (g=10m/s^2)
View SolutionA skater of mass m standing on ice throws a stone of mass M with a velocity of v in a horizontal direction. The distance over which the skater will move back (the coefficient of friction between the skater and the ice is μ)
View SolutionA boy of mass 25 kg stands on a board of mass 10 kg which in turn is kept on a frictionless horizontal ice surface. The boy makes a jump with a velocity component 5m/s in a horizontal direction with respect to the ice. With what velocity does the board recoil? With what rate are the boy and the board seperate from each other?
View Solution
