A bullet of mass 20g and moving with 600ms collides with a block of mass 4kg hanging with the string. What is the velocity of bullet when it comes out of block, if block rises to height 0.2m after collision?
200ms−1
150ms−1
400ms−1
300ms−1
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Calculate the initial momentum of the bullet.
The initial momentum of the bullet can be calculated using the formula:
Pinitial=mbullet×vbullet
Where:
- mbullet=20g=0.02kg (converted to kg)
- vbullet=600m/s
Calculating:
Pinitial=0.02kg×600m/s=12kg m/s
Step 2: Use conservation of momentum.
According to the conservation of momentum:
Pinitial=Pfinal
The final momentum can be expressed as:
Pfinal=mbullet×v+mblock×v′
Where:
- v is the velocity of the bullet after it exits the block.
- v′ is the velocity of the block after the collision.
Given:
- mblock=4kg
Thus, we can write:
12=0.02v+4v′
This is our Equation 1.
Step 3: Calculate the velocity of the block after the collision using conservation of energy.
The block rises to a height of h=0.2m. The potential energy gained by the block is equal to the kinetic energy it had just after the collision.
Using the conservation of energy:
12mv′2=mgh
Where:
- m=4kg
- g=10m/s2 (approximate value for gravitational acceleration)
- h=0.2m
Cancelling m from both sides:
12v′2=gh
v′2=2gh
v′=√2gh=√2×10×0.2=√4=2m/s
Step 4: Substitute v′ back into Equation 1.
Now, substitute v′=2m/s into Equation 1:
12=0.02v+4(2)
12=0.02v+8
0.02v=12−8
0.02v=4
v=40.02=200m/s
Final Answer
The velocity of the bullet when it comes out of the block is 200m/s.
---
The initial momentum of the bullet can be calculated using the formula:
Pinitial=mbullet×vbullet
- mbullet=20g=0.02kg (converted to kg)
- vbullet=600m/s
Pinitial=0.02kg×600m/s=12kg m/s
According to the conservation of momentum:
Pinitial=Pfinal
Pfinal=mbullet×v+mblock×v′
- v is the velocity of the bullet after it exits the block.
- v′ is the velocity of the block after the collision.
- mblock=4kg
12=0.02v+4v′
This is our Equation 1.
The block rises to a height of h=0.2m. The potential energy gained by the block is equal to the kinetic energy it had just after the collision.
12mv′2=mgh
- m=4kg
- g=10m/s2 (approximate value for gravitational acceleration)
- h=0.2m
12v′2=gh
v′2=2gh
v′=√2gh=√2×10×0.2=√4=2m/s
Now, substitute v′=2m/s into Equation 1:
12=0.02v+4(2)
12=0.02v+8
0.02v=12−8
0.02v=4
v=40.02=200m/s
The velocity of the bullet when it comes out of the block is 200m/s.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A bullet of mass m and velocity v is fired into a large block of mass M. The final velocity of the system is
View SolutionA ball of mass 0.50 kg moving at a speed of 5.0 m/s collides with another ball of mas 1.0 kg. After the collision the balls stick together ane remain motionless. What was the velocity of the 1.0 kg block before the collision?
View SolutionA block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass A and velocity B is fired into a wooden block of mass C. If the bullet geta embedded in the wooden block.then velocity of wooden block after collision
View SolutionA bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View SolutionA bullet of mass 0.01 kg and travelling at a speed of 500 m/s strikes a block of mass 2 kg which is suspended by a string of length 5m. The center of gravity of the block is found to rise a vertical distance of 0.1m, figure. What is the speed of the bullet after it emerges from the block ? (g=9.8m/s2).
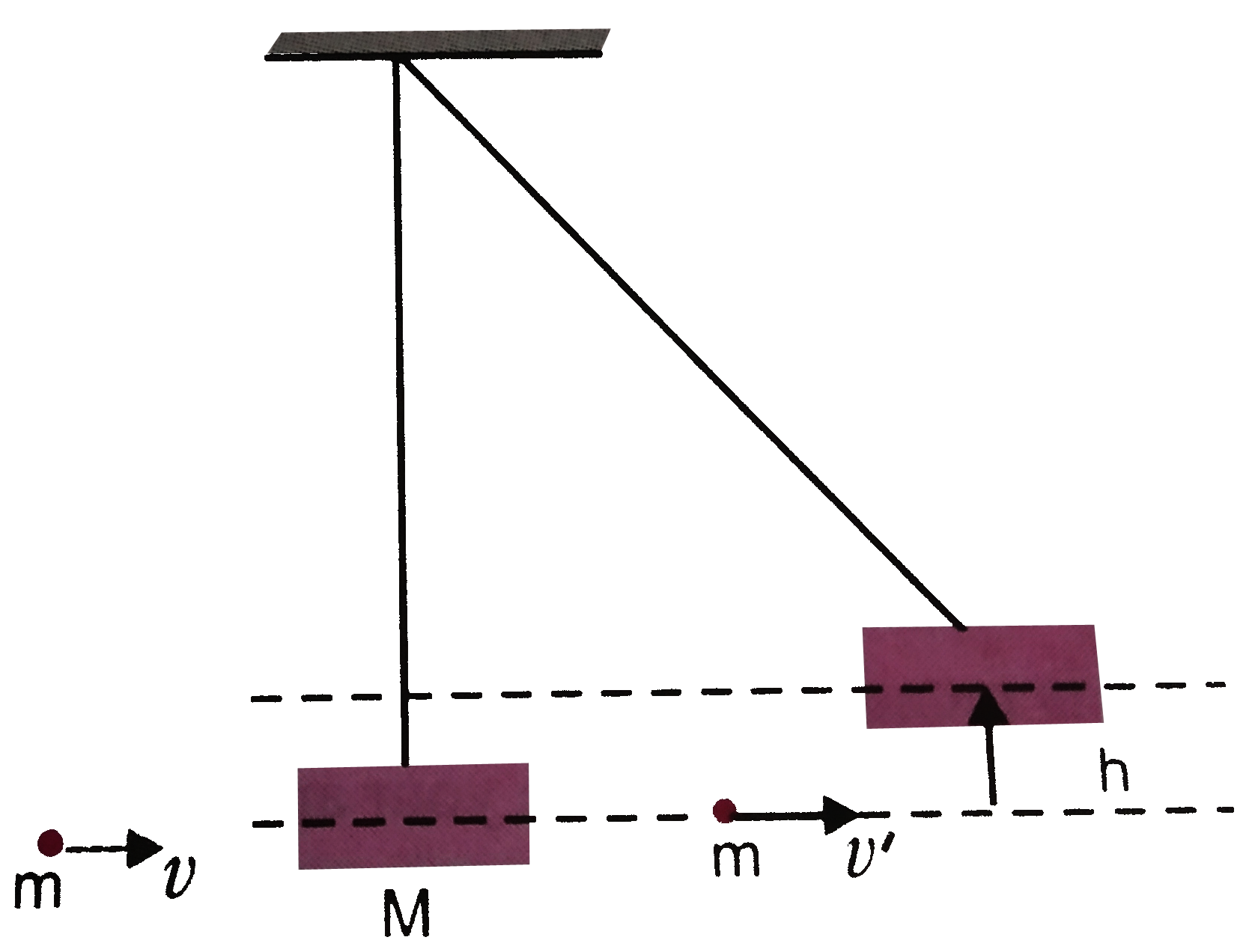
View SolutionA block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionIf a bullet of mass 5gm moving with velocity 100m/sec, penertates the wooden block upto 6cm. Then the average force imposed by the bullet on the block is
View Solution
