A bullet of mass m and velocity v is fired into a large block of mass M. The final velocity of the system is
Mm+M.v
mm+M.v
m+Mm.v
None of these
The correct Answer is:B
To solve the problem of finding the final velocity of a system consisting of a bullet fired into a large block, we can use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Understand the System
We have a bullet of mass m moving with a velocity v, and a large block of mass M that is initially at rest.
Step 2: Identify Initial Momentum
Before the bullet hits the block, the initial momentum Pi of the system can be calculated as:
Pi=momentum of bullet+momentum of block
Since the block is at rest, its momentum is zero. Thus,
Pi=mv+0=mv
Step 3: Identify Final Momentum
After the bullet embeds itself into the block, they move together as a single system. The total mass of this combined system is:
m′=M+m
Let the final velocity of the system after the collision be v′. The final momentum Pf is then:
Pf=(M+m)v′
Step 4: Apply Conservation of Momentum
According to the law of conservation of momentum, the initial momentum must equal the final momentum:
Pi=Pf
Substituting the expressions we derived:
mv=(M+m)v′
Step 5: Solve for Final Velocity
To find the final velocity v′, we can rearrange the equation:
v′=mvM+m
Conclusion
Thus, the final velocity of the system after the bullet is fired into the block is:
v′=mvM+m
We have a bullet of mass m moving with a velocity v, and a large block of mass M that is initially at rest.
Before the bullet hits the block, the initial momentum Pi of the system can be calculated as:
Pi=momentum of bullet+momentum of block
Since the block is at rest, its momentum is zero. Thus,
Pi=mv+0=mv
After the bullet embeds itself into the block, they move together as a single system. The total mass of this combined system is:
m′=M+m
Let the final velocity of the system after the collision be v′. The final momentum Pf is then:
Pf=(M+m)v′
According to the law of conservation of momentum, the initial momentum must equal the final momentum:
Pi=Pf
Substituting the expressions we derived:
mv=(M+m)v′
To find the final velocity v′, we can rearrange the equation:
v′=mvM+m
Thus, the final velocity of the system after the bullet is fired into the block is:
v′=mvM+m
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A bullet of mass A and velocity B is fired into a wooden block of mass C. If the bullet geta embedded in the wooden block.then velocity of wooden block after collision
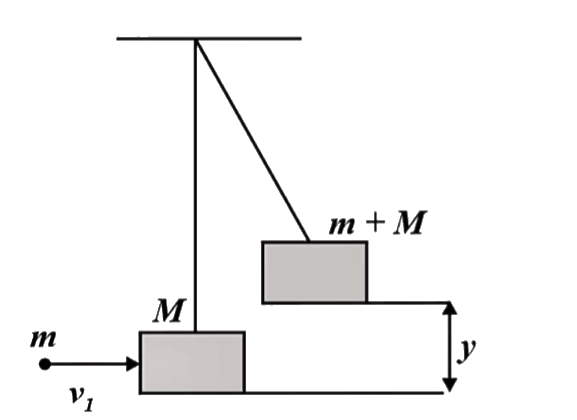
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionFrom a rifle of mass 4kg, a bullet of mass 50g is fired with an initial velocity of 35m/s. Calculate the initial recoil velocity of the rifle.
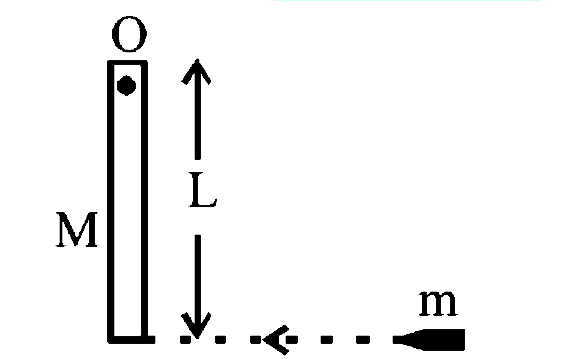
View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.
View SolutionA bullet of mass 'm' moving with velocity 'u' passes through a wooden block of mass M=nm as shown in figure. The block is resting on a smooth horizontal floor. After passing through the block, velocity relative to the block is
 .
.
View SolutionA frequently used device to measure the speed of bullets is the ballistic pendulum. It comprises of a heavy block of wood of mass M suspended by two long chords. A bullet of mass m is fired into the block horizontally. The block, with the bullet embedded in it, swings upwards. The centre of mass of the combination rises through a vertical distance h before coming to rest momentarily. In a particular experiment, a bullet of mass 40 gm is fired into a wooden block of mass 10 kg. The block is observed to rise by a height of 20.0 cm.
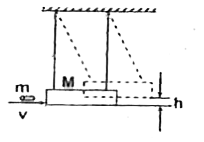
Initial speed of the bullet is
View SolutionA bullet of mass 20g and moving with 600ms collides with a block of mass 4kg hanging with the string. What is the velocity of bullet when it comes out of block, if block rises to height 0.2m after collision?
View SolutionA frequently used device to measure the speed of bullets is the ballistic pendulum. It comprises of a heavy block of wood of mass M suspended by two long chords. A bullet of mass m is fired into the block horizontally. The block, with the bullet embedded in it, swings upwards. The centre of mass of the combination rises through a vertical distance h before coming to rest momentarily. In a particular experiment, a bullet of mass 40 gm is fired into a wooden block of mass 10 kg. The block is observed to rise by a height of 20.0 cm.
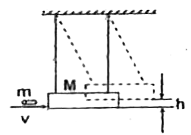
If the bullet penetrates the block to a depth of 3.0 cm, the approximate average force of resistance by the block of wood is
View SolutionA bullet of mass m is fired into a block of wood of mass M which hangs on the end of pendulum and gets embedded into it. When the bullet strikes with maximum rise R. Then, the velocity of the bullet is given by
View Solution
