A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
v22g(mM+m)2
v22g(M+mm)2
v22g(mM)2
v22g(Mm)2
The correct Answer is:A
To solve the problem of a bullet embedding into a block of wood and determining the height to which the block rises, we can follow these steps:
1. Understand the System:
- We have a bullet of mass m moving with velocity v.
- The bullet strikes a block of wood of mass M which is hanging from the ceiling by a massless string.
- After the collision, the bullet gets embedded in the block.
2. Conservation of Momentum:
- Before the collision, the momentum of the bullet is mv and the block is at rest (momentum = 0).
- After the collision, the combined mass of the bullet and block is (M+m) and let v1 be their common velocity after the collision.
- According to the conservation of momentum:
mv+0=(M+m)v1
- Rearranging gives:
v1=mvM+m
3. Conservation of Energy:
- At the moment just after the bullet embeds in the block, all kinetic energy is converted to potential energy at the maximum height h.
- The total kinetic energy just after the collision is:
KE=12(M+m)v21
- The potential energy at the height h is:
PE=(M+m)gh
- Setting the kinetic energy equal to the potential energy gives:
12(M+m)v21=(M+m)gh
4. Solving for Height h:
- We can cancel (M+m) from both sides (assuming M+m≠0):
12v21=gh
- Rearranging for h:
h=v212g
5. Substituting for v1:
- Substitute v1=mvM+m into the equation for h:
h=(mvM+m)22g
- Simplifying gives:
h=m2v2(M+m)2⋅2g
Final Result:
The height to which the block rises is:
h=m2v22g(M+m)2
- We have a bullet of mass m moving with velocity v.
- The bullet strikes a block of wood of mass M which is hanging from the ceiling by a massless string.
- After the collision, the bullet gets embedded in the block.
- Before the collision, the momentum of the bullet is mv and the block is at rest (momentum = 0).
- After the collision, the combined mass of the bullet and block is (M+m) and let v1 be their common velocity after the collision.
- According to the conservation of momentum:
mv+0=(M+m)v1
- Rearranging gives:
v1=mvM+m
- At the moment just after the bullet embeds in the block, all kinetic energy is converted to potential energy at the maximum height h.
- The total kinetic energy just after the collision is:
KE=12(M+m)v21
- The potential energy at the height h is:
PE=(M+m)gh
- Setting the kinetic energy equal to the potential energy gives:
12(M+m)v21=(M+m)gh
- We can cancel (M+m) from both sides (assuming M+m≠0):
12v21=gh
- Rearranging for h:
h=v212g
- Substitute v1=mvM+m into the equation for h:
h=(mvM+m)22g
- Simplifying gives:
h=m2v2(M+m)2⋅2g
The height to which the block rises is:
h=m2v22g(M+m)2
Topper's Solved these Questions
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT
18 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON
15 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass 0.012 kg and horizontal speed 70ms−1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by thin wire. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
View SolutionA bullet of mass m moving vertically upwards instantaneously with a velocity 'u' hits the hanging block of mass 'm' and gets embedded in it, as shown in the figure. The height through which the block rises after the collision. (assume sufficient space above block) is:
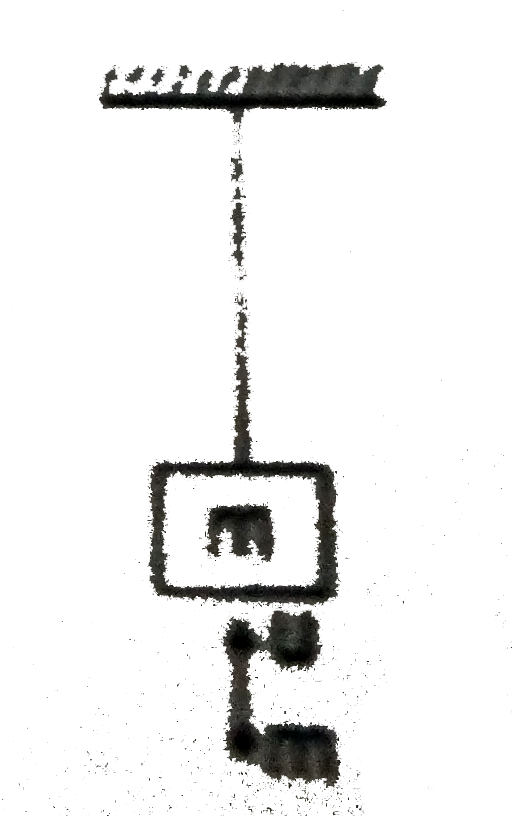
View SolutionA bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.

View SolutionA bullet of mass 0.25kg is fired with velocity 302m/s into a block of wood of mass m1=37.5kg. It gets embedded into it. The block m1 is resting on a long block m2 and the horizontal surface on which it is placed is smooth. The coefficient of friction between m1 and m2 is 0.5. Find the displacement of m1 on m2 and the common velocity of m1 and m2. Mass m2=1.25kg.
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View SolutionBallistic Pendulum: A ballistic pendulum is used to measure speed of bullets. It consists of a wooden blocksuspended from fixed support.
A wooden block mass M is suspended with the help of two threads to prevent rotation while swinging. A bullet of mass m moving horizontally with velocity v0 hits the block and becomes embedded in the block. Receiving momentum from the bullet, the bullet in terms of given quatities.

View SolutionA bullet of mass 10g moving horizontally with a velocity of 400ms−1 strickes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5m. As a result, the center ofgravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out hirizontally from the block will be
View SolutionA bullet of mass 10g moving horizontally with a velocity of 400ms−1 strickes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5m. As a result, the center ofgravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out hirizontally from the block will be
View SolutionA bullet of mass A and velocity B is fired into a wooden block of mass C. If the bullet geta embedded in the wooden block.then velocity of wooden block after collision
View Solution
