A capacitor of capacitance is connected to a battery of emf 2V.It is found that it takes 50 ms for the charge on the capacitor to bacome find the resistance of the circuit.
To solve the problem step by step, we will use the formula for the charging of a capacitor in an RC circuit:
Step 1: Identify the given values
- Capacitance, C=10μF=10×10−6F
- EMF of the battery, V=2V
- Charge on the capacitor at time t=50ms=50×10−3s
- Charge on the capacitor, Q=12.6μC=12.6×10−6C
Step 2: Calculate the maximum charge Qmax
The maximum charge Qmax on the capacitor can be calculated using the formula:
Qmax=C⋅V
Substituting the values:
Qmax=(10×10−6F)⋅(2V)=20×10−6C
Step 3: Use the charging equation of the capacitor
The charge on the capacitor at time t is given by:
Q=Qmax(1−e−tRC)
Substituting the known values:
12.6×10−6=20×10−6(1−e−50×10−3R⋅10×10−6)
Step 4: Rearranging the equation
Divide both sides by 20×10−6:
12.620=1−e−50×10−3R⋅10×10−6
Calculating 12.620:
0.63=1−e−50×10−3R⋅10×10−6
Rearranging gives:
e−50×10−3R⋅10×10−6=1−0.63=0.37
Step 5: Taking the natural logarithm
Taking the natural logarithm of both sides:
−50×10−3R⋅10×10−6=ln(0.37)
Now, calculate ln(0.37):
ln(0.37)≈−0.994
Substituting this back into the equation:
−50×10−3R⋅10×10−6=−0.994
Step 6: Solve for R
Multiplying both sides by −1:
50×10−3R⋅10×10−6=0.994
Cross-multiplying gives:
50×10−3=0.994⋅R⋅10×10−6
Now, solving for R:
R=50×10−30.994⋅10×10−6=50×10−39.94×10−6≈5.03kΩ
Final Answer
The resistance of the circuit is approximately 5.03kΩ.
---
- Capacitance, C=10μF=10×10−6F
- EMF of the battery, V=2V
- Charge on the capacitor at time t=50ms=50×10−3s
- Charge on the capacitor, Q=12.6μC=12.6×10−6C
The maximum charge Qmax on the capacitor can be calculated using the formula:
Qmax=C⋅V
Substituting the values:
Qmax=(10×10−6F)⋅(2V)=20×10−6C
The charge on the capacitor at time t is given by:
Q=Qmax(1−e−tRC)
Substituting the known values:
12.6×10−6=20×10−6(1−e−50×10−3R⋅10×10−6)
Divide both sides by 20×10−6:
12.620=1−e−50×10−3R⋅10×10−6
Calculating 12.620:
0.63=1−e−50×10−3R⋅10×10−6
Rearranging gives:
e−50×10−3R⋅10×10−6=1−0.63=0.37
Taking the natural logarithm of both sides:
−50×10−3R⋅10×10−6=ln(0.37)
Now, calculate ln(0.37):
ln(0.37)≈−0.994
Substituting this back into the equation:
−50×10−3R⋅10×10−6=−0.994
Multiplying both sides by −1:
50×10−3R⋅10×10−6=0.994
Cross-multiplying gives:
50×10−3=0.994⋅R⋅10×10−6
Now, solving for R:
R=50×10−30.994⋅10×10−6=50×10−39.94×10−6≈5.03kΩ
The resistance of the circuit is approximately 5.03kΩ.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
An uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(ii) time at which the rate has time miximum value is
View SolutionA capacitor of capacitance 6 μF is connected with an emf sourface 3 V. Electrostaci energy stored in the capacitor is
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionA capacitor gets a charge of 60μC when it is connected to a battery of emf 12 V. Calculate the capacitance of the capactor.
View SolutionA capacitor of capacitance C=2.0±0.1μF is charged to a voltage V=20±0.2V. What will be the charge Q on the capacitor ? Use Q=CV.
View SolutionA capacitor is connected to a 12 V battery through a resistance of (10Ω).It is found that the potential difference across the capacitor rises to 4.0 V in 1(mu)s. find the capacitance of the capacitor.
View SolutionA capacitor of capacitance 100(μ)F is connected across a battery of emf6.0V through a resistance of 20k(Ω)for 4.0s after the battery is disconnecting?
View SolutionAn uncharged capacitor is connected to a 15 V battery through a resistance of 10Ω. It is found that in a time of 2μs, potential difference across the capacitor becomes 5V. Find the capacitance of the Capacitor. Take ln(1.5) = 0.4.
View SolutionIn the circuit shown , charge on the 5μF capacitor is :
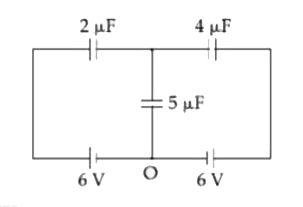
View Solution
