A capacitor of capacity C is connected with a battery of potential V in parallel. The distance between its plates is reduced to half at one, assuming that the charge remains the same. Then to charge the capacitance upto the potential V again, the energy given by the battery will be
CV2/4
CV2/2
2CV2/4
CV2
The correct Answer is:D
To solve the problem step by step, we will analyze the situation involving the capacitor, its capacitance, charge, and the energy supplied by the battery.
Step 1: Understand the Initial Conditions
- A capacitor of capacitance C is connected to a battery of potential V.
- The initial charge Q on the capacitor can be calculated using the formula:
Q=C⋅V
Step 2: Change in Capacitance
- When the distance between the plates of the capacitor is reduced to half, the new capacitance C′ can be calculated using the formula:
C′=Aϵ0D/2=2C
- Thus, the new capacitance C′ is double the original capacitance.
Step 3: Charge on the New Capacitor
- Since the capacitor is still connected to the same battery, the charge on the new capacitor Q′ when fully charged will be:
Q′=C′⋅V=2C⋅V=2Q
- Here, Q′ is twice the initial charge Q.
Step 4: Charge Adjustment
- To maintain the same charge Q as before, we need to remove some charge from the capacitor. The amount of charge that needs to be removed ΔQ is:
ΔQ=Q′−Q=2Q−Q=Q
Step 5: Energy Supplied by the Battery
- The energy W supplied by the battery to remove this charge ΔQ at potential V is given by:
W=ΔQ⋅V=Q⋅V
- Substituting Q=C⋅V:
W=(C⋅V)⋅V=CV2
Step 6: Final Result
- Therefore, the energy given by the battery to charge the capacitor up to potential V again is:
W=CV2
- A capacitor of capacitance C is connected to a battery of potential V.
- The initial charge Q on the capacitor can be calculated using the formula:
Q=C⋅V
- When the distance between the plates of the capacitor is reduced to half, the new capacitance C′ can be calculated using the formula:
C′=Aϵ0D/2=2C
- Thus, the new capacitance C′ is double the original capacitance.
- Since the capacitor is still connected to the same battery, the charge on the new capacitor Q′ when fully charged will be:
Q′=C′⋅V=2C⋅V=2Q
- Here, Q′ is twice the initial charge Q.
- To maintain the same charge Q as before, we need to remove some charge from the capacitor. The amount of charge that needs to be removed ΔQ is:
ΔQ=Q′−Q=2Q−Q=Q
- The energy W supplied by the battery to remove this charge ΔQ at potential V is given by:
W=ΔQ⋅V=Q⋅V
- Substituting Q=C⋅V:
W=(C⋅V)⋅V=CV2
- Therefore, the energy given by the battery to charge the capacitor up to potential V again is:
W=CV2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
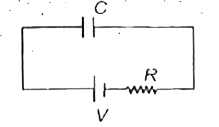
As in the figure, if a capacitor of capacitance 'C' is charged by connecting it with resistance R, then energy given by the battery will be
View SolutionA capacitor gets a charge of 60μC when it is connected to a battery of emf 12 V. Calculate the capacitance of the capactor.
View SolutionAnswer the following:
(a) Describe briefly the process of transferring charge between the two plates of a parallel plate capacitor when connected to a battery. Derive an expression for the energy stored in a capacitor.
(b) A parallel plate capacitor is connected to a battery of potential difference V. It is disconnected from battery and then connected to another uncharged capacitor of the same capacitance. Calculate the ratio of the energy stored in the combination to the initial energy on the single capacitor.
View SolutionA parallel plate capacitor of capacitance C has been charged, so that the potential difference between its plates is V. Now, the plates of this capacitor are connected to another uncharged capacitor of capacitance 2C. Find the common potential acquired by the system and loss of energy.
View SolutionA capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then

View SolutionA battery is used to charge a parallel plate capacitor till the potential differece between the plates becomes equal to the electromotive force of the battery. The ratio of the energy stored in the capacitor and the work done by the battery will be
View SolutionA capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 300 μC. When potential across the capacitor is reduced by 100 V, the charge stored in it becomes 100 μC. Calculate the potential V and the unknown capacitance. What will be the charge stored in the capacitor if the voltage applied had increased by 100V?
View SolutionA capacitor of capacitance 10μF is charged to a potential 50V with a battery. The battery is now disconnected and an additional charge 200μC is given to the positive plate of the capacitor. The potential difference across the capacitor will be.
View SolutionA parallel plate capacitor of capacitance C is connected to a battery and is charged to a potential difference V. Another capacitor of capacitance 2C is ismilarly charged to a potential difference 2V. The charging battery is now disconnected and the capacitors are connected in parallel to each other in such a way that the poistive terminal of one is connected to the negative terminal of the other. The final energy of the configuration is
View SolutionThe parallel combination of two air filled parallel plate capacitor of capacitance C and nC is connected to a battery of voltage, V. When the capacitors are fulley charged, the battery is removed and after that a dielectric material of dielectric constant K is placed between the two plates of the first capacitors. the new potential difference of the combined system is
View Solution
