A capacitor stores 50μc charge when connected across a battery . When the gap between the plates is filled with a dielectric , a charge of 100muc flows through the battery .Find the dielectric constant of the material inserted.
To solve the problem step by step, we can follow these steps:
Step 1: Understand the Initial Condition
Initially, the capacitor stores a charge Q1=50μC when connected to a battery.
Step 2: Identify the Final Condition
When a dielectric is inserted, an additional charge of Qadded=100μC flows through the battery. Therefore, the final charge on the capacitor becomes:
Qf=Q1+Qadded=50μC+100μC=150μC
Step 3: Relate Charge, Capacitance, and Voltage
The relationship between charge Q, capacitance C, and voltage V is given by:
Q=C⋅V
For the initial condition:
Q1=C⋅V(1)
For the final condition, when the dielectric is inserted, the capacitance becomes C′=K⋅C, where K is the dielectric constant. Therefore:
Qf=C′⋅V=K⋅C⋅V(2)
Step 4: Substitute the Values
From equation (1), we know that C⋅V=50μC. We can substitute this into equation (2):
150μC=K⋅(50μC)
Step 5: Solve for the Dielectric Constant K
Rearranging the equation gives:
K=150μC50μC=3
Conclusion
The dielectric constant K of the material inserted is 3.
---
Initially, the capacitor stores a charge Q1=50μC when connected to a battery.
When a dielectric is inserted, an additional charge of Qadded=100μC flows through the battery. Therefore, the final charge on the capacitor becomes:
Qf=Q1+Qadded=50μC+100μC=150μC
The relationship between charge Q, capacitance C, and voltage V is given by:
Q=C⋅V
For the initial condition:
Q1=C⋅V(1)
For the final condition, when the dielectric is inserted, the capacitance becomes C′=K⋅C, where K is the dielectric constant. Therefore:
Qf=C′⋅V=K⋅C⋅V(2)
From equation (1), we know that C⋅V=50μC. We can substitute this into equation (2):
150μC=K⋅(50μC)
Rearranging the equation gives:
K=150μC50μC=3
The dielectric constant K of the material inserted is 3.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
A capacitor stores 60μC charge when connected across a battery. When the gap between the plates is filled with a dielectric, a charge of 120μC flows through the battery. The dielectric constant of the material inserted is:
View SolutionA parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionA capacitor gets a charge of 60μC when it is connected to a battery of emf 12 V. Calculate the capacitance of the capactor.
View SolutionA parallel-plate capacitor having plate are 100cm2 and separation 1.0 mm holds a charge of 0.12μC when connected to a 120 V battery. Find the dielectric constant of the material filling the gap.
View SolutionTwo parallel plate capacitors of capacitance C each are connected in series with a battery of emf ε. Then, one of the capacitors is filled with a dielectric of dielectric constane K.
i. Find the change in electric field in the two capacitors, if any
ii. What amount of charge flows through the battery?
iii Find the change in the energy stored in the circuit, if any.
View SolutionThree plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is
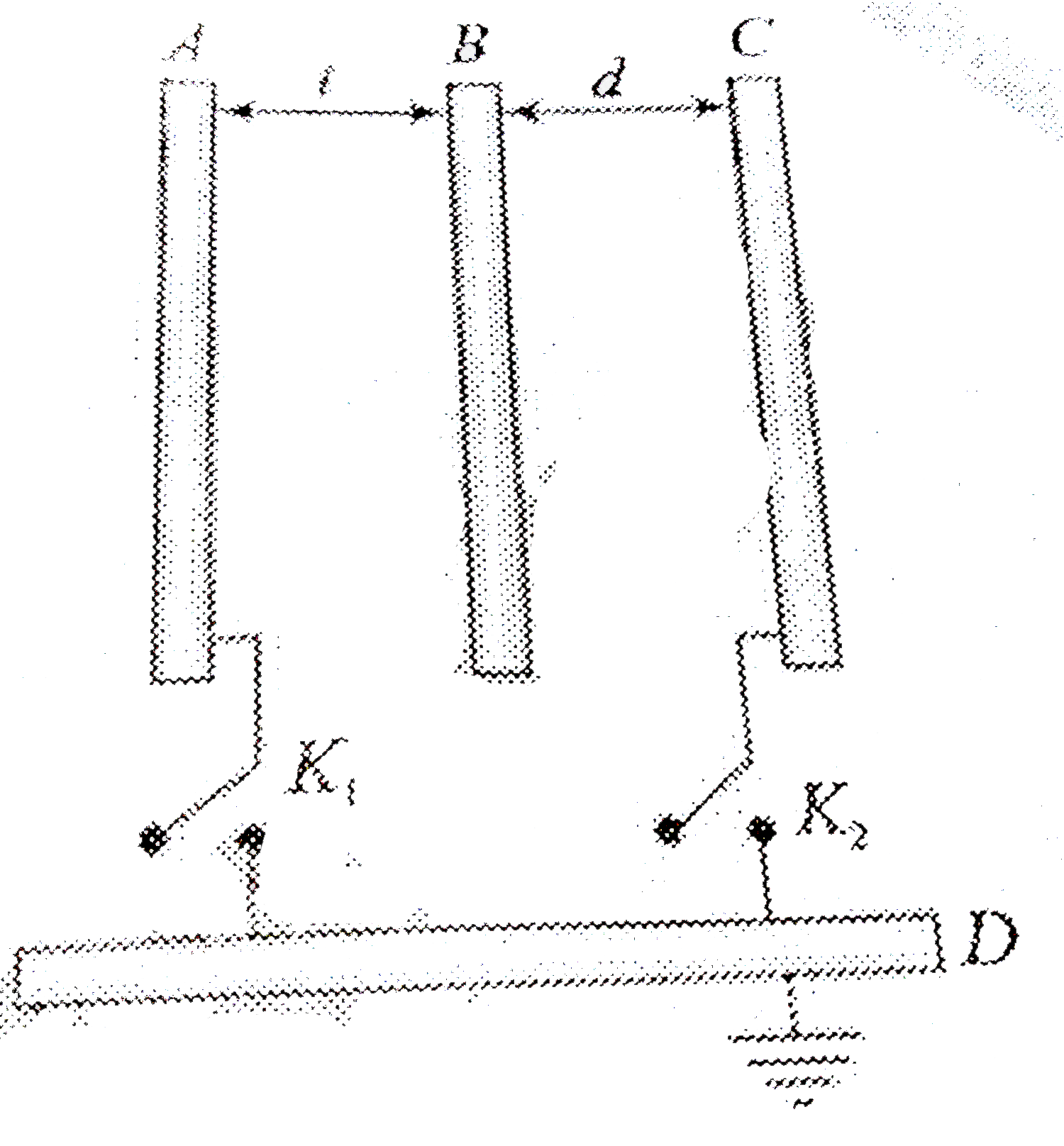
View SolutionAn air filled parallel plate capacitor of capacitance 50μF is connected to a battery of 100 V. A slab of dielectric constant 4 is inserted in it to fill the space completely . Find the extra charge flown through the battery till it attains the steady state.
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionA parallel plate capacitar, of capacitance, 20μF, is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
View Solution
