A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
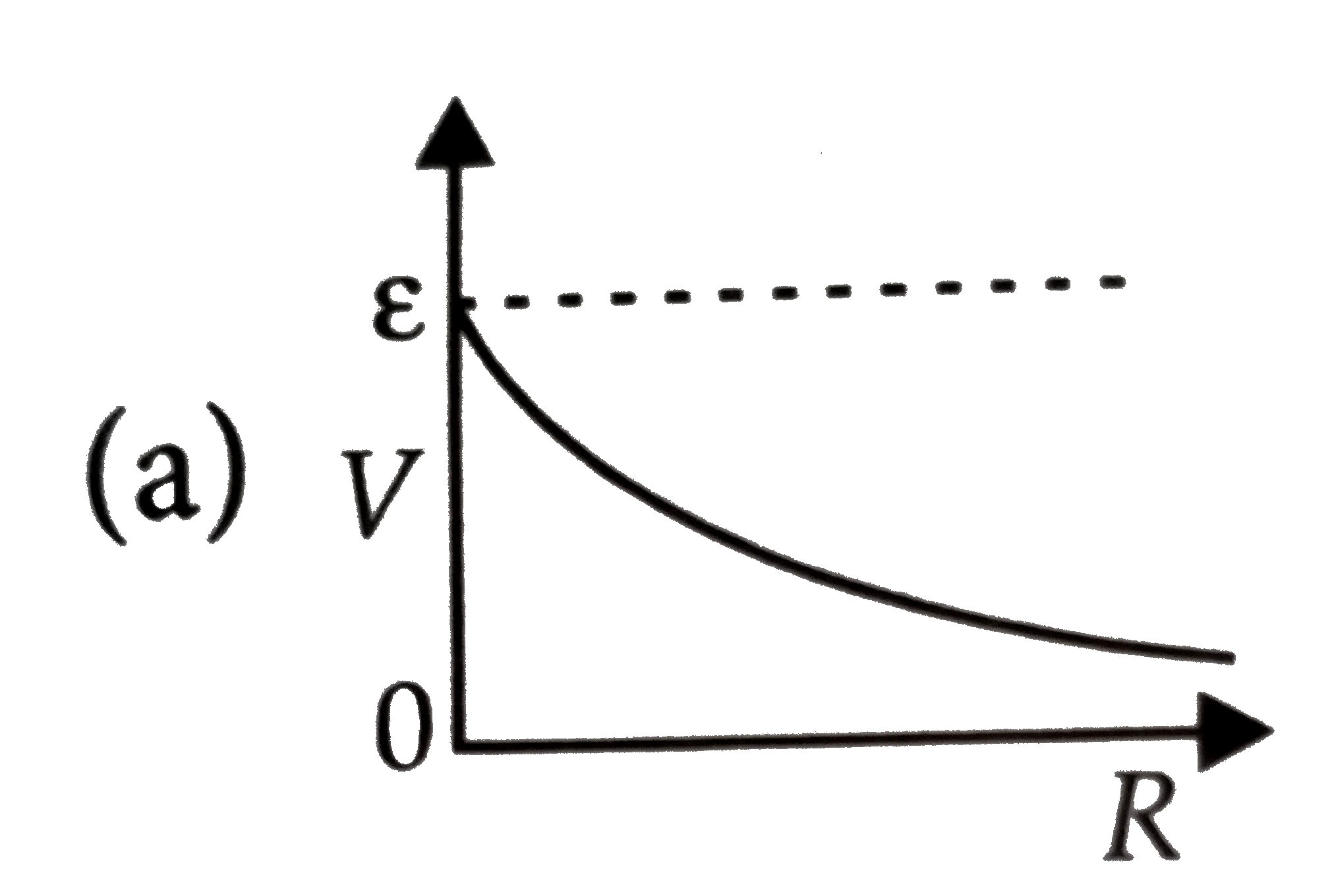
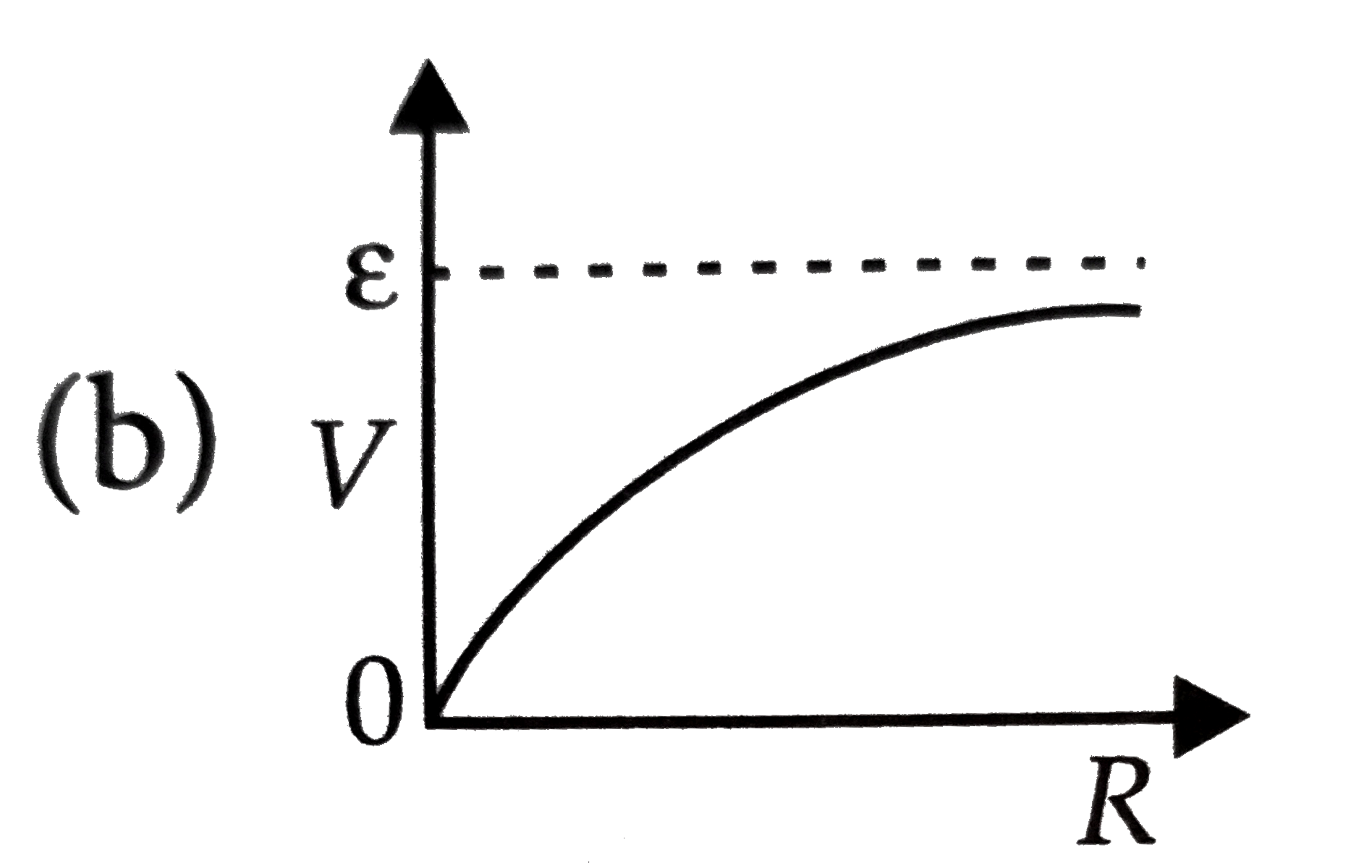
The correct Answer is:B
To solve the problem, we need to analyze how the potential difference V across the external resistance R changes as R is increased. We will use the relationship between the electromotive force (emf) E, the internal resistance r, and the external resistance R.
1. Understanding the Circuit:
- We have a cell with an emf E and internal resistance r.
- The cell is connected to a variable external resistance R.
2. Current in the Circuit:
- The total resistance in the circuit is R+r.
- The current I flowing through the circuit can be expressed as:
I=ER+r
3. Potential Difference Across External Resistance:
- The potential difference V across the external resistance R can be calculated using Ohm's law:
V=I⋅R
- Substituting the expression for I:
V=(ER+r)R
- This simplifies to:
V=E⋅RR+r
4. Analyzing the Behavior of V:
- As R increases, we need to analyze the behavior of V:
- When R=0:
V=E⋅00+r=0
- When R approaches infinity:
V = \frac{E \cdot R}{R + r} \rightarrow E \quad \text{(as R becomes very large)}
5. Graphical Representation:
- The potential difference V starts at 0 when R=0 and approaches E as R increases indefinitely.
- Therefore, the graph of V versus R will start at the origin (0,0) and asymptotically approach E as R increases.
6. Conclusion:
- The correct plot of potential difference V across R as R is increased is a curve that starts at the origin and approaches the value E.
- We have a cell with an emf E and internal resistance r.
- The cell is connected to a variable external resistance R.
- The total resistance in the circuit is R+r.
- The current I flowing through the circuit can be expressed as:
I=ER+r
- The potential difference V across the external resistance R can be calculated using Ohm's law:
V=I⋅R
- Substituting the expression for I:
V=(ER+r)R
- This simplifies to:
V=E⋅RR+r
- As R increases, we need to analyze the behavior of V:
- When R=0:
V=E⋅00+r=0
- When R approaches infinity:
V = \frac{E \cdot R}{R + r} \rightarrow E \quad \text{(as R becomes very large)}
- The potential difference V starts at 0 when R=0 and approaches E as R increases indefinitely.
- Therefore, the graph of V versus R will start at the origin (0,0) and asymptotically approach E as R increases.
- The correct plot of potential difference V across R as R is increased is a curve that starts at the origin and approaches the value E.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - KIRCHOFF S LAW
14 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - WHEATSTONE BRIDGE
6 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - COMBINED OF RESISTORS;
23 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason
30 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
Similar Questions
2A cell having an emf ε and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionA cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View SolutionA cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation o P.D. Across R, verses 'R.
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionA cell of e.m.f E and internal resitance r ,is connected to an external resistance R. the variation of potential difference V across the resistance R as function of R as shown in the figure, is the best represented by curve
_PHY_E01_011_Q01.png)
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionA battery of e.m.f. 10V and internal resistance 0.5ohm is connected across a variable resistance R. The value of R for which the power delivered in it is maximum is given by
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View Solution
