A charged 30 μF capacitor is connected to a 27 mH inductor. What is the angular frequency of free oscillations of the circuit ?
To find the angular frequency of free oscillations of a circuit consisting of a capacitor and an inductor, we can use the formula for angular frequency (ω) in an LC circuit:
ω=1√LC
1. Identify the values of Capacitance (C) and Inductance (L):
- Given capacitance C=30μF=30×10−6F
- Given inductance L=27mH=27×10−3H
2. Substitute the values into the formula:
- Plug in the values of L and C into the formula for angular frequency:
ω=1√(27×10−3)×(30×10−6)
3. Calculate the product LC:
- First, calculate LC:
LC=(27×10−3)×(30×10−6)=810×10−9=8.1×10−7
4. Calculate the square root of LC:
- Now, find √LC:
√LC=√8.1×10−7≈9.0×10−4
5. Calculate the angular frequency ω:
- Now, substitute back to find ω:
ω=19.0×10−4≈1111.11rad/s
6. Final Result:
- Therefore, the angular frequency of free oscillations of the circuit is approximately:
ω≈1.1×103rad/s
Conclusion:
The angular frequency of free oscillations of the circuit is 1.1×103rad/s.
- Given capacitance C=30μF=30×10−6F
- Given inductance L=27mH=27×10−3H
- Plug in the values of L and C into the formula for angular frequency:
ω=1√(27×10−3)×(30×10−6)
- First, calculate LC:
LC=(27×10−3)×(30×10−6)=810×10−9=8.1×10−7
- Now, find √LC:
√LC=√8.1×10−7≈9.0×10−4
- Now, substitute back to find ω:
ω=19.0×10−4≈1111.11rad/s
- Therefore, the angular frequency of free oscillations of the circuit is approximately:
ω≈1.1×103rad/s
The angular frequency of free oscillations of the circuit is 1.1×103rad/s.
Topper's Solved these Questions
Similar Questions
An 8(μ)F capacitor is connected across a 220√2 V, 50 Hz line. What is the peak value of charge through the capacitor?
View SolutionA capacitor of capacitance 25μF is charged to 300V. It is then connected across a 10mH inductor. The resistance in the circuit is negligible.
a. Find the frequency of oscillation of the circuit.
b. Find the potential difference across capacitor and magnitude of circuit current 1.2ms after the inductor and capacitor are connected.
c. Find the magnetic energy and electric energy at t=0 and t=1.2ms.View Solution
Knowledge Check
- Question 1 - Select One
A circuit containing a 20Ω resistor and 0.1μF capacitor in series is connected to 320 V ac supply of angular frequency 100 rad s−1. The impedance of the circuit is
A105ΩB104ΩC106ΩD1010Ω - Question 2 - Select One
A 30μF capacitor is connected to a 150 V, 60 Hz ac supply. The rms value of current in the circuit is
A17 AB1.7AC1.7mAD2.7A
A capacitor with capacitance 6×10−5F is charged by connecting it to a 12−V battery. The capacitor is disconnected from the battery and connected across an inductor with L=1.50H.
a. What are the angular frequency ω of the electrical oscillations and the period of these oscillations (the time for one oscillation)?
b. What is the intial charge on the capacitor?
c. How much energy is intially stored in the capacitor?
d. What is the charge on the capacitor 0.0230 s after the connecting to the inductor is made? Interpret the sign of the your answer.
e. At the times given in part (d), what is the current in the inductor? Interpret the sign of your answer.
f. At the time given in part (d), how much electrical energy is stored in the capactior and how much is stored in the inductor?View SolutionInitially, the capacitor is charged to a potential of 5V and then connected to position 1 with the shown polarity for 1s. After 1s it is connected across the inductor at position 2
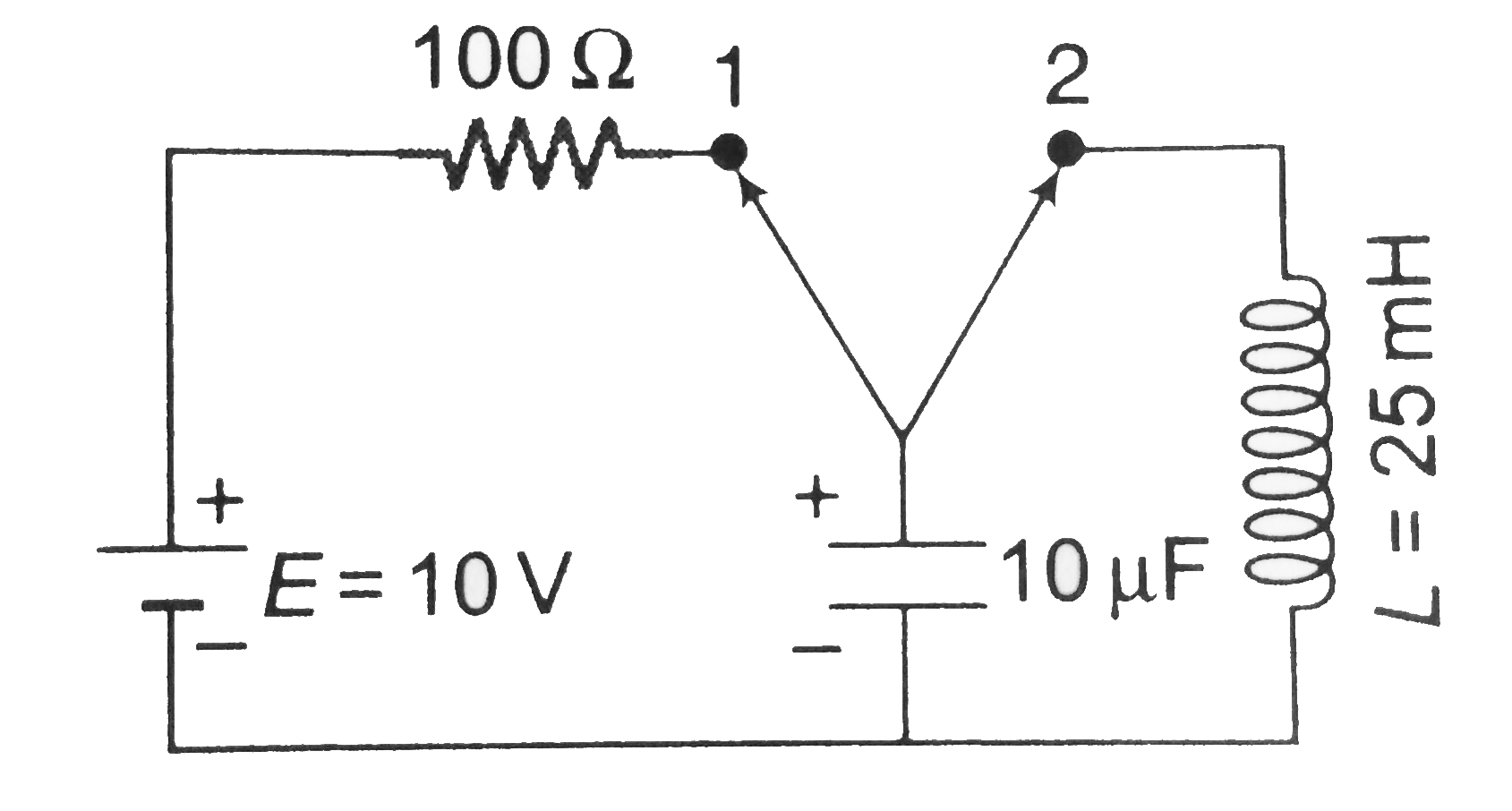
(a) Find the potential across the capacitor after 1s of its connection to position 1.
(b) Find the maximum current flowing in the L−C circuit when capacitor is connected across the inductor. Also, find the frequency of LC oscillations.View SolutionThe charge in the 2μF capacitor at steady state is
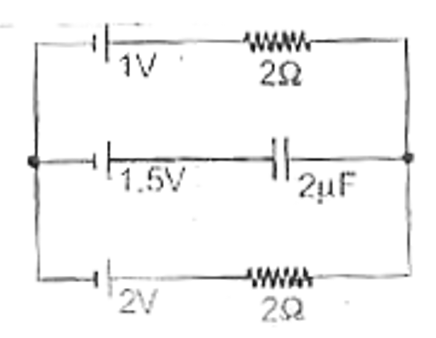 View Solution
View SolutionA 1.00μF capacitor is charged by a 40.0V power supply. The fully charged charged capacitor is then discharged through a 10.0mH inductor. Find the maximum current in the resultaing oscillations.
View SolutionIn the circuit in Fig. switch S1 was closed for a long time . At time t=0 the switch is opened.
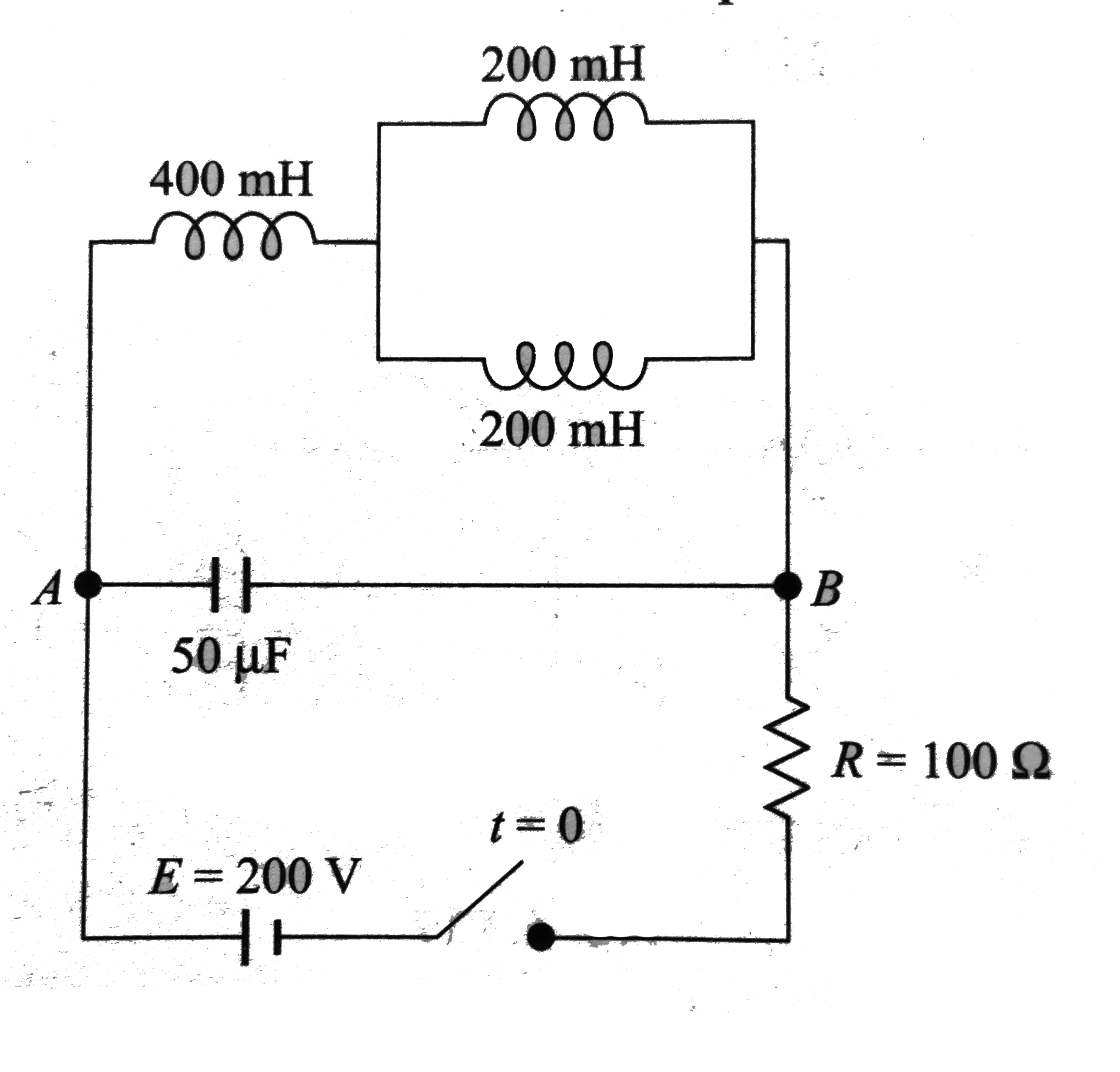
Find the angular frequency of oscillation of the charge on the capacitor.View SolutionA 15.0μF capacitor is connected to a 220 V, 50 Hz source. Find the capactive reactance and the current (rms and peak) in the circuit. If the frequency is doubled. What happens to the capactive reactance and current ?
View Solution

