A charged particle of mass 5×10−5kg is held stationary in space by placing it in an electric field of strength 107NC−1 directed vertically downwards. The charge on the particle is
−20×10−5μC
−5×10−5μC
5×10−5μC
20×10−5μC
The correct Answer is:B
To solve the problem, we need to find the charge on a particle that is held stationary in an electric field. The steps to find the solution are as follows:
Step 1: Understand the forces acting on the charged particle
The charged particle experiences two forces:
1. The gravitational force (weight) acting downwards, given by Fg=mg.
2. The electric force acting upwards, given by Fe=QE.
Step 2: Set up the equilibrium condition
Since the particle is stationary, the upward electric force must balance the downward gravitational force:
Fe=Fg
This can be expressed as:
QE=mg
Step 3: Substitute known values
We know:
- Mass m=5×10−5kg
- Acceleration due to gravity g≈10m/s2
- Electric field strength E=107N/C
Substituting these values into the equation gives:
Q⋅107=(5×10−5)⋅10
Step 4: Calculate the gravitational force
Calculating the gravitational force:
Fg=mg=(5×10−5kg)⋅(10m/s2)=5×10−4N
Step 5: Solve for the charge Q
Now we can rearrange the equilibrium equation to solve for Q:
Q=FgE=5×10−4107
Q=5×10−4×10−7=5×10−11C
Step 6: Convert to microcoulombs
Since the problem asks for the charge in microcoulombs, we convert:
1C=106μC
Thus,
Q=5×10−11C=5×10−5μC
Step 7: Determine the sign of the charge
Since the electric force must act upwards to balance the weight (which acts downwards), the charge must be negative (as the electric field is directed downwards).
Final Answer
The charge on the particle is:
Q=−5×10−5μC
---
The charged particle experiences two forces:
1. The gravitational force (weight) acting downwards, given by Fg=mg.
2. The electric force acting upwards, given by Fe=QE.
Since the particle is stationary, the upward electric force must balance the downward gravitational force:
Fe=Fg
This can be expressed as:
QE=mg
We know:
- Mass m=5×10−5kg
- Acceleration due to gravity g≈10m/s2
- Electric field strength E=107N/C
Q⋅107=(5×10−5)⋅10
Calculating the gravitational force:
Fg=mg=(5×10−5kg)⋅(10m/s2)=5×10−4N
Now we can rearrange the equilibrium equation to solve for Q:
Q=FgE=5×10−4107
Q=5×10−4×10−7=5×10−11C
Since the problem asks for the charge in microcoulombs, we convert:
1C=106μC
Thus,
Q=5×10−11C=5×10−5μC
Since the electric force must act upwards to balance the weight (which acts downwards), the charge must be negative (as the electric field is directed downwards).
The charge on the particle is:
Q=−5×10−5μC
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.2
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A sphere of mass 50 gm is suspended by a string in an electric field of intensity 5NC−1 acting vertically upward. If the tension in the string is 520 millinewton, the charge on the sphere is (g=10ms−2)
View SolutionA particle of mass 2×10−3 kg, charge 4×10−3C enters in an electric field of 5V/m, then its kinetic energy after 10 s is
View Solution
Knowledge Check
A particle of mass 10−3kg and charge 5μC is thrown at a speed of 20ms−1 against a uniform electric field of strength 2×105NC−1. The distance travelled by particle before coming to rest is
A0.1 mB0.2 mC0.3 mD0.4 m
A particle of mass 1 g and charge 2.5×10−4C is released from rest in an electric field of 1.2×104NC−1 (a) Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis? (b) How long will it take for the particle to travel a distance of 40 cm? (c) What will be the speed of the particle after travelling this destance? (d) how much is the work done by electric force on the particle during this period?
View SolutionA charged oil drop weighing 1.6×10−15N is found to remain suspended in a uniform electric field of intensity 2×103NC−1. Find the charge on the drop.
View SolutionA sphere of mass 50gm is suspended by a string in an electric field of intensity 5NC−1 acting vertically upward. If the tension in the string is 520 milli newton, the charge on the sphere is (g=10ms−2)
View SolutionTwo circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field E=105NC−1 directed vertically upward as shown in figure. Distance between centers of the rings A and B (CAandCB)is40cm. Ring A has positive charge qA=10μC and B has a negative charge qB=−20μC. A particle of mass m and charge q=10μC is released from rest at the center of ring A. If particle moves along CACB, then

Work done by electric field, when particle moves from CA→CB is
View SolutionTwo circular rings A and B each of radius a = 30 cm are placed coaxially with their axis horizontal in a uniform electric field E=105NC−1 directed vertically upward as shown in figure. Distance between centers of the rings A and B (CAandCB)is40cm. Ring A has positive charge qA=10μC and B has a negative charge qB=−20μC. A particle of mass m and charge q=10μC is released from rest at the center of ring A. If particle moves along CACB, then
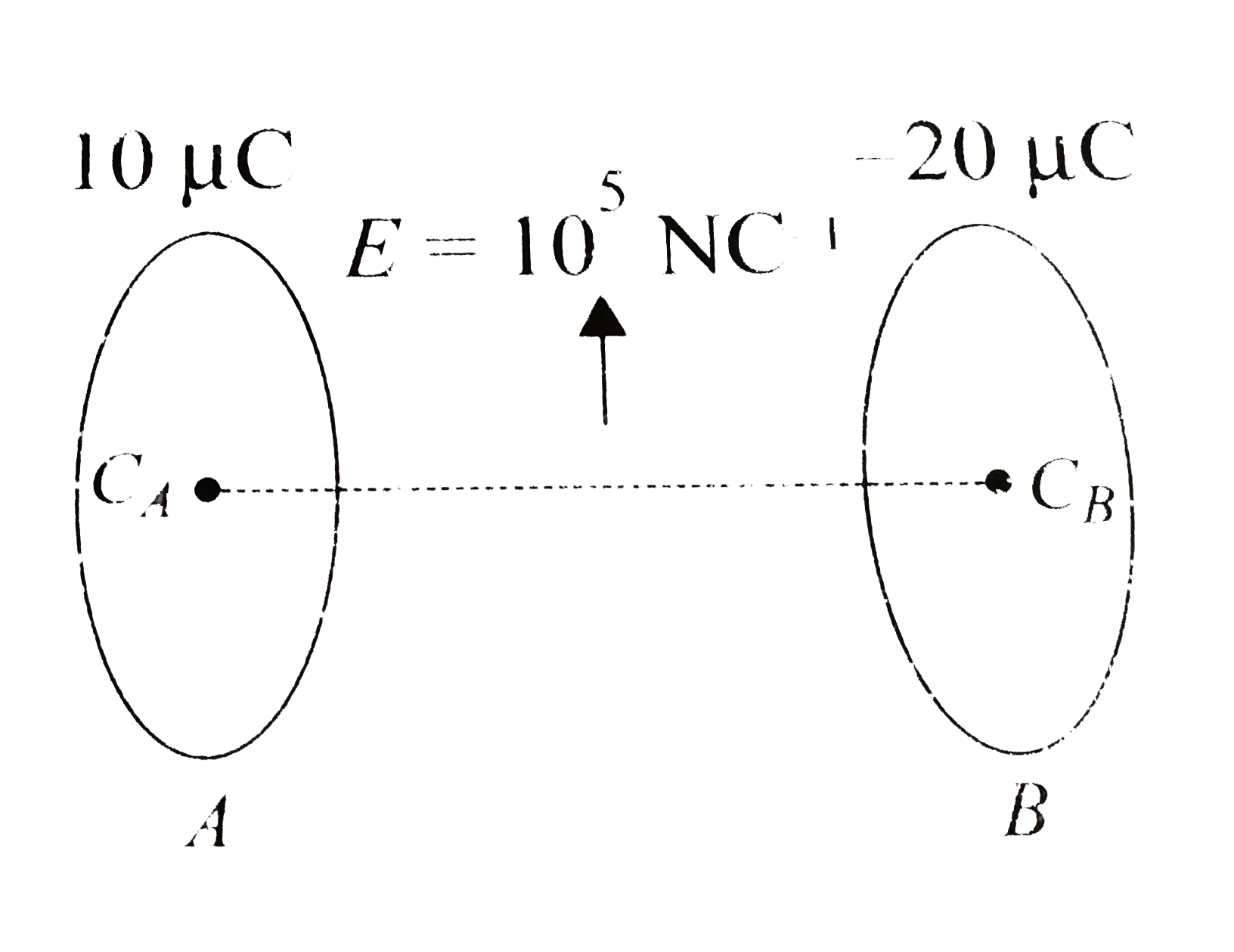
Speed of particle when it reaches at center of B is
View SolutionA Charged particle of mass 1.0 g is suspended through a
. silk thread of length 40 cm in a horizantal electric field
. of 4.0×104NC−1 . If the particle stays aty a distance of
. 24 cm from the wall in equilibrium, find the charge on
. the particle.
View SolutionA particle of mass m=1.6×10−27 kg and charge q=1.6×10−19C enters a region of uniform magnetic field of stregth 1T along the direction shown in figure. The speed of the particle is 107m/s

a. The magnetic field is directed along the inward normal to the plane of the paper. The particle leaves the region of the fiedl at the point F. Find the distasnce EF and the angle theta.
b. If the direction of the field is along the outward normal to the plane of the paper find the time spent by the particle in the regin of the magnetic field after entering it at E.
View Solution
