A choke coil of resistance 5Ω and inductance 0.6 H is in series with a capacitance of 10(μ)F. If a voltage of 200 V is applied and the frequency is adjusted to resonance, the current and voltage across the inductance and capacitance are (I0),(V0)and(V1) respectively. we have
(I0)=40A
(V0)=9.8kV
(V1)=9.8kV
(V1)=19.6kV
The correct Answer is:A, B, C
To solve the problem, we will follow these steps:
Step 1: Determine the Current at Resonance
At resonance in an RLC circuit, the inductive reactance XL equals the capacitive reactance XC. The formula for the current I in the circuit is given by:
I=V√R2+(XC−XL)2
Since XC=XL at resonance, the formula simplifies to:
I0=VR
Given:
- Voltage V=200V
- Resistance R=5Ω
Substituting the values:
I0=2005=40A
Step 2: Calculate the Inductive Reactance XL
The inductive reactance XL is given by:
XL=ωL
Where ω=2πf. To find XL, we first need to calculate the resonant frequency f.
Step 3: Calculate the Resonant Frequency f
The resonant frequency f is given by:
f=12π√LC
Given:
- Inductance L=0.6H
- Capacitance C=10μF=10×10−6F
Substituting the values:
f=12π√0.6×10×10−6
Calculating:
f≈12π√6×10−7≈12π×0.000775≈65Hz
Step 4: Calculate XL
Now, substituting f into the equation for XL:
XL=2πfL=2π(65)(0.6)≈245Ω
Step 5: Calculate the Voltage Across the Inductor V0
The voltage across the inductor V0 is given by:
V0=I0⋅XL
Substituting the values:
V0=40⋅245=9800V=9.8kV
Step 6: Calculate the Voltage Across the Capacitor V1
The capacitive reactance XC is given by:
XC=1ωC
Substituting ω and C:
XC=12π(65)(10×10−6)
Calculating XC:
XC≈12π(65)(10−5)≈245Ω
Now, the voltage across the capacitor V1 is:
V1=I0⋅XC=40⋅245=9800V=9.8kV
Final Results
- I0=40A
- V0=9.8kV
- V1=9.8kV
At resonance in an RLC circuit, the inductive reactance XL equals the capacitive reactance XC. The formula for the current I in the circuit is given by:
- Voltage V=200V
- Resistance R=5Ω
The inductive reactance XL is given by:
The resonant frequency f is given by:
- Inductance L=0.6H
- Capacitance C=10μF=10×10−6F
Now, substituting f into the equation for XL:
The voltage across the inductor V0 is given by:
The capacitive reactance XC is given by:
- I0=40A
- V0=9.8kV
- V1=9.8kV
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Assertion-reasoning
7 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Linked Comprehension
25 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Single Correct
63 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
A choke coil of resistance R and inductance is connected to an ac. source of frequency f and peak voltage V If angular frequency will increase then, the average power dissipated in the choke
View SolutionIn a series resonant circuit, the ac, voltage across resistance R, inductance L and capacitance are 5V, 10V and 10V, respectively. The ac. voltage applied to the circuit will be
View SolutionA series LCR circuit containing a resistance of 120Ω has angular resonance frequency 4×105rads−1. At resonance the vlotage across resistance and inductance are 60V and 40 V, repectively,
The value of capacitance C is
View SolutionA series LCR circuit containing a resistance of 120Ω has angular resonance frequency 4×105rads−1. At resonance the vlotage across resistance and inductance are 60V and 40 V, repectively,
the value of inductance L is
View SolutionIn LC oscillation resistance is 100 Ω and inductance and capacitance is 1 H and 10μF . Find the half power of frequency .
View SolutionA series LCR circuit containing a resistance of 120 ohm has angular resonance frequency 4×103rads−1. At resonance, the voltage across resistance and inductance are 60V and 40 V respectively. The values of Land C are respectively
View SolutionA coil having a resistance of 5 Ω and an inductance of 0.02H is arranged in parallel with another coil having a resistance of 1Ω and an inductance of 0.08H. Calculate the power absorbed when a voltage of 100V at 50Hz is applied.
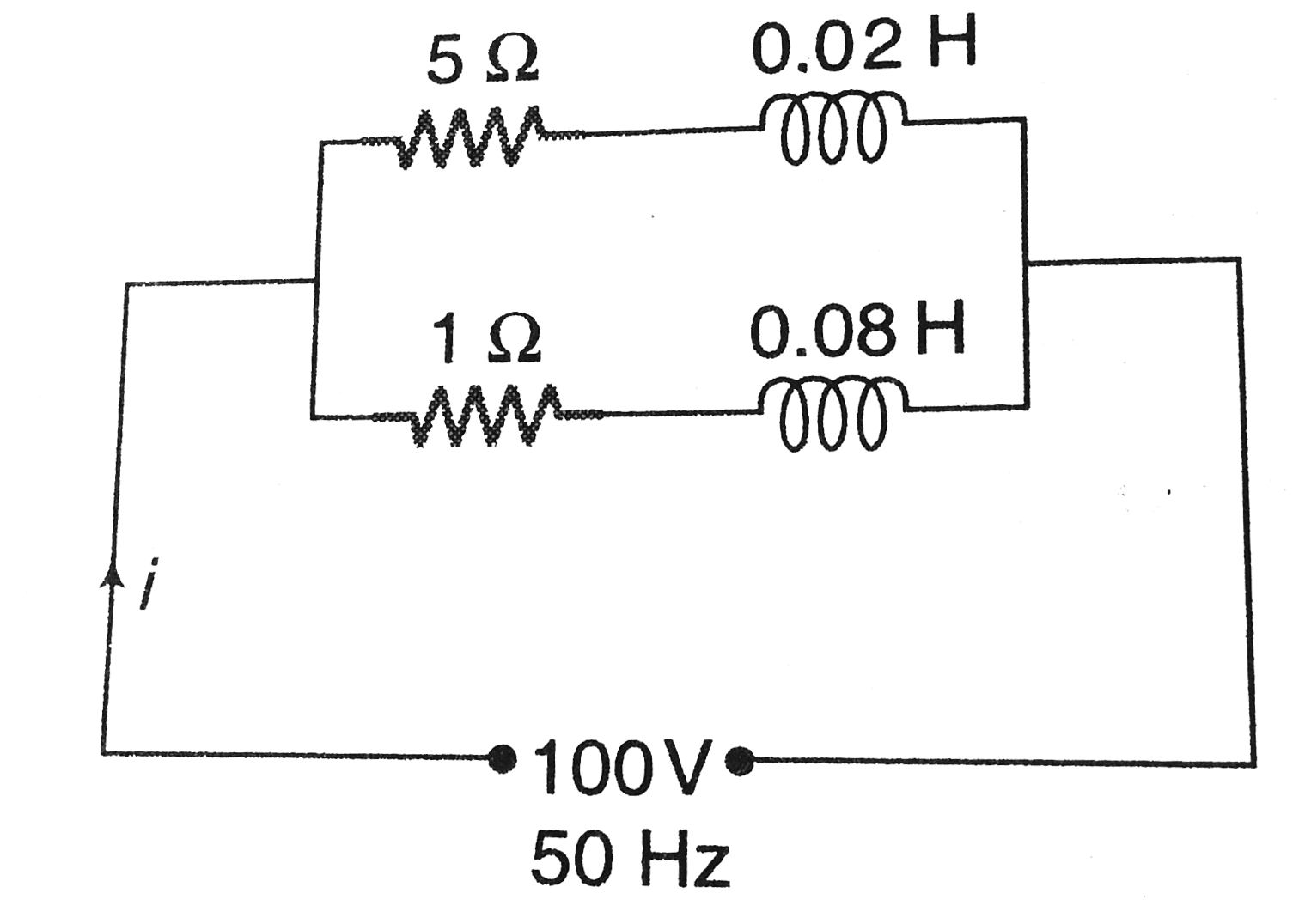 .
.
View SolutionA capacitor of capacitance 100μF and a coil of resistance 50Ω and inductance 0.5H are connected in series with a110V,50HzAC source. Find the rms value of the current.
View SolutionIn a series L−C circuit, the applied voltage is V0. if omega is very low, then the voltage drop across the inductor VL and capacitor VC are
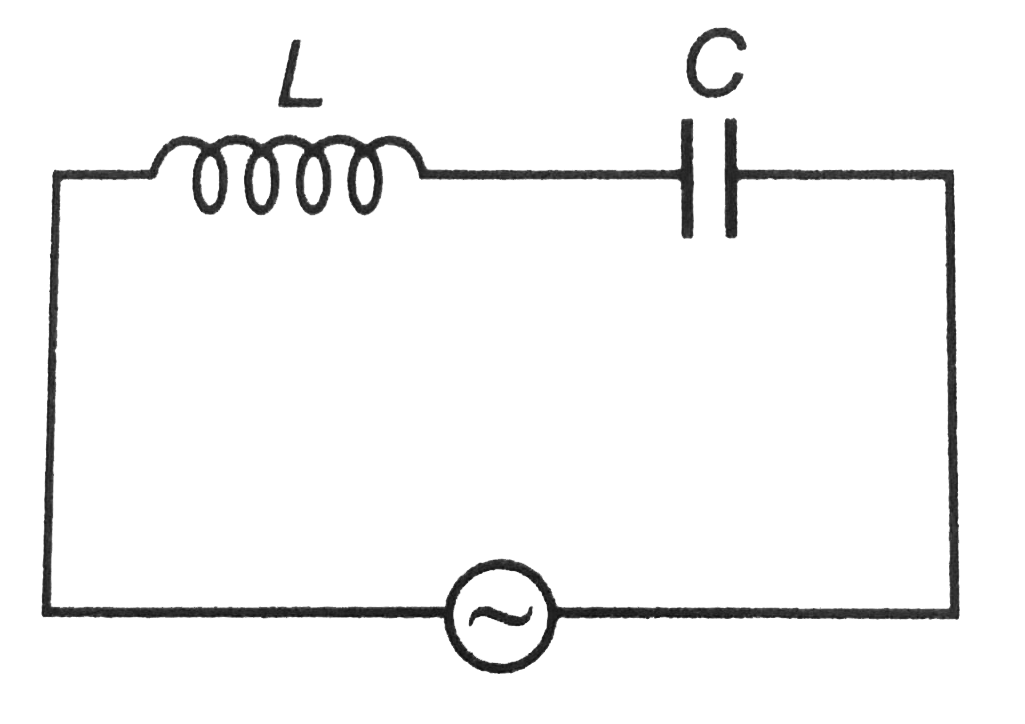 .
.
View SolutionA coil of resistance 300Ω and inductance 1.0 henry is connected across an voltages source of frequency 300/2πHz. The phase difference between the voltage and current in the circuit is
View Solution
