A circuit with capacitance $C$ and inductance $L$ generates free damped oscillations with current varying with time as $I = I_{m} e^{- β t} \sin ω t$ . Find the voltage across the capacitor as a function of time, and in particular, at the moment $t = 0$ .

Video Solution

Text Solution

Verified by Experts

We write
$- \frac{d Q}{d t} = I = I_{m} e^{- β t} \sin ω t$
$= g m I_{m} e^{- β t + i ω t}$ (gm means imaginary part )
Then $Q = g m I_{m} \frac{e^{- β t + i ω t}}{- β + i ω}$
$Q = g m I_{m} \frac{e^{- β t + i ω t}}{β - i ω}$
$= g m I_{m} \frac{(β + i ω) e^{- β t + i ω t}}{β^{2} + ω^{2}}$
$= I_{m} e^{- β t} \frac{β \sin ω t + ω \cos ω t}{β^{2} + ω^{2}}$
$= I_{m} e^{- β t} \frac{\sin (ω t + δ)}{\sqrt{β^{2} + ω^{2}}}, \tan δ = \frac{ω}{β}$
( An arbitrary constant of integration has been put equal to zero. )
Thus $V = \frac{Q}{C} = I_{m} \sqrt{\frac{L}{C}} e^{- β t} \sin (ω t + δ)$
$V (0) = I_{m} \sqrt{\frac{L}{C}} \sin δ = I_{m} \sqrt{\frac{L}{c}} \frac{ω}{\sqrt{ω^{2} + β^{2}}}$
$= I_{m} \sqrt{\frac{L}{C (1 + β^{2} / ω^{2})}}$

Updated on:21/07/2023

|

Class 12 PHYSICS OSCILLATIONS AND WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Figure shows the variation of voltage with time for an ac $I = I_{0} sin ω t$ flowing through a circuit -

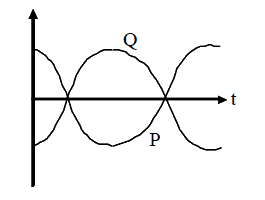ACurve P is for R–L and Q for R–C circuit
BCurve P is for R–C and Q for R–L circuit
CBoth are for R–C circuit
DBoth are for R–L circuit

IE IRODOV, LA SENA & SS KROTOV-OSCILLATIONS AND WAVES-Electric Oscillations

Home
Ask Doubt
Profile