A coil of wire with cross-sectional area 0.50 mm2 weighs 75 N in air and 65 N in water. The length of the coil in cm is (Take g = 10 m/s2)
10250
10200.50
1065
1050.0050
The correct Answer is:C
To find the length of the coil, we can use the information provided about the weight of the coil in air and water. Here’s a step-by-step solution:
Step 1: Understand the problem
We know the weight of the coil in air (W_air = 75 N) and in water (W_water = 65 N). The difference in weight when submerged in water is due to the buoyant force acting on it.
Step 2: Calculate the buoyant force
The buoyant force (B) can be calculated as:
B=Wair−Wwater
B=75N−65N=10N
Step 3: Use Archimedes' principle
According to Archimedes' principle, the buoyant force is equal to the weight of the fluid displaced by the coil. The weight of the water displaced can be expressed as:
B=Volumedisplaced×Densitywater×g
Where:
- Densitywater=1000kg/m3
- g=10m/s2
Step 4: Relate volume to the cross-sectional area and length
The volume of the coil can be expressed in terms of its cross-sectional area (A) and length (L):
Volume=A×L
Given that the cross-sectional area A=0.50mm2=0.50×10−6m2.
Step 5: Set up the equation
Now we can substitute the volume into the buoyant force equation:
B=A×L×Densitywater×g
Substituting the known values:
10N=(0.50×10−6m2)×L×(1000kg/m3)×(10m/s2)
Step 6: Solve for L
Now we can solve for L:
10=(0.50×10−6)×L×10000
10=5×10−3×L
L=105×10−3
L=2000m
Step 7: Convert L to cm
To convert L from meters to centimeters:
L=2000m=2000×100cm=200000cm
Final Answer
The length of the coil is 200000cm.
---
We know the weight of the coil in air (W_air = 75 N) and in water (W_water = 65 N). The difference in weight when submerged in water is due to the buoyant force acting on it.
The buoyant force (B) can be calculated as:
B=Wair−Wwater
B=75N−65N=10N
According to Archimedes' principle, the buoyant force is equal to the weight of the fluid displaced by the coil. The weight of the water displaced can be expressed as:
B=Volumedisplaced×Densitywater×g
Where:
- Densitywater=1000kg/m3
- g=10m/s2
The volume of the coil can be expressed in terms of its cross-sectional area (A) and length (L):
Volume=A×L
Given that the cross-sectional area A=0.50mm2=0.50×10−6m2.
Now we can substitute the volume into the buoyant force equation:
B=A×L×Densitywater×g
Substituting the known values:
10N=(0.50×10−6m2)×L×(1000kg/m3)×(10m/s2)
Now we can solve for L:
10=(0.50×10−6)×L×10000
10=5×10−3×L
L=105×10−3
L=2000m
To convert L from meters to centimeters:
L=2000m=2000×100cm=200000cm
The length of the coil is 200000cm.
Topper's Solved these Questions
Similar Questions
Find the emf induced in a coil of 200 turns and cross-sectional area 0.2m2, when a magnetic field perpendicular to the plane of the coil changes from 0.1Wbm−2→0.5Wbm−2 at a uniform rate over a period of 0.05 s.
View SolutionA circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the
(a) Total torque on the coil,
(b) Total force on the coil,
(c) Aerage force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10−5m2, and the free electron density in copper is given to be about 1029m−3) .View Solution
Knowledge Check
- Question 1 - Select One
A rubber cord of cross-sectional area 2 cm2 has a length of 1 m. When a tensile force of 10 N is applied, the length of the cord increases by 1 cm. What is the Young's modulus of rubber ?
A2×106N/m2B5×106N/m2C0.5×106N/m2D0.2×106N/m2 - Question 2 - Select One
A cylindrical tank is filled with water to a level of 3m. A hole is opened at a height of 52.5 cm from bottom. The ratio of the area of the hole to that of cross-sectional area of the cylinder is 0.1. The square of the speed with which water is coming out from the orifice is (Take g=10m/s2)
A50m2/s2B40m2/s2C51.5m2/s2D50.5m2/s2 - Question 3 - Select One
The level of water in a tank is 5 m high. A hole of area of cross section 1 cm2 is made at the bottom of the tank. The rate of leakage of water for the hole in m3s−1 is (g=10ms−2)
A10−3B10−4C10D10−2
A steel rod of cross-sectional area 1m2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2
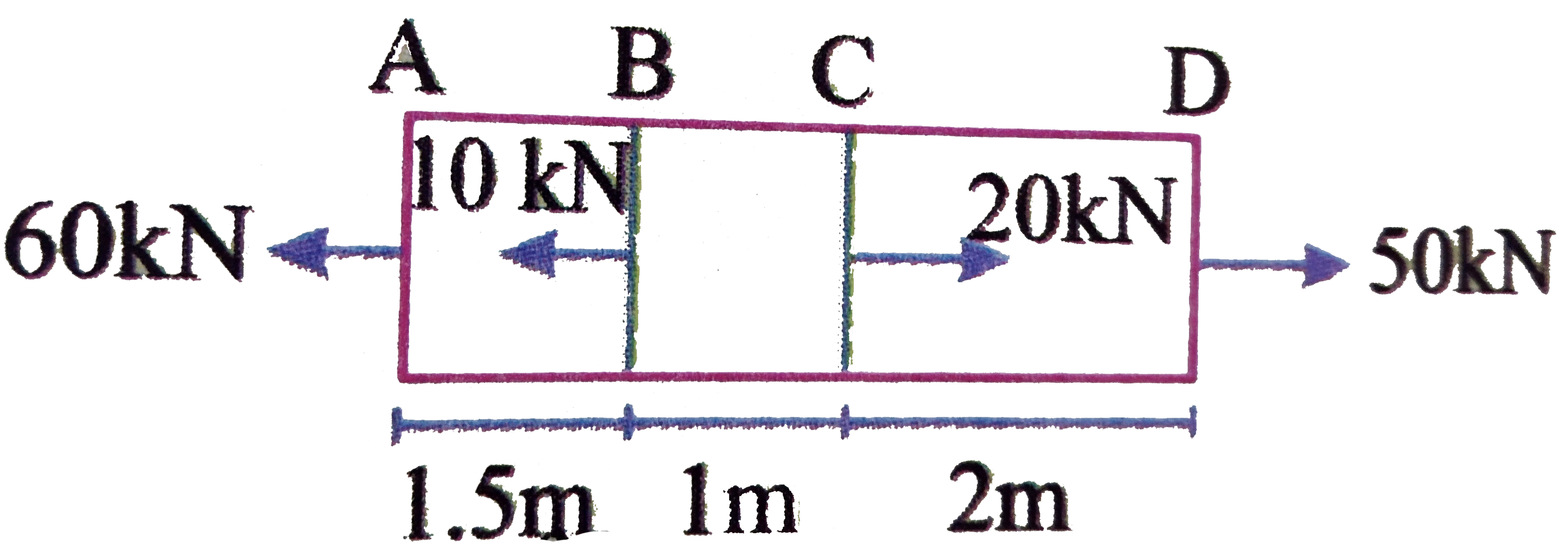 View Solution
View SolutionA circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the coil. If the current in the coil is5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due to the magnetic field? (The coil is made of copper wire of cross sectional area 10−5m2 and the free electron density in copper is given to be about 1029m−3 )View SolutionA body weight 20 N in water and 30 N in air. Find the density of the body. Take the density of water as 1.0gcm−3.
View SolutionA brass of length 2m and cross-sectional area 2.0cm2 is attached end to end to a steel rod of length and cross-sectional area 1.0cm2. The compound rod is subjected to equal and oppsite pulls of magnitude 5×104N at its ends. If the elongations of the two rods are equal, the length of the steel rod (L) is
{YBrass=1.0×1011N/m2 and Ysteel=2.0×1011N/m2View SolutionA resistance of 50Ω is to be prepared using a wire of cross-sectional area 10−8m2 and conductivity 2.2×106 siemens/metre. The length of the wire required is
View Solution
