A coin is placed at the bottom of a glass trough containing water (refractive index = 43 ) up to a height 20 cm. At what depth it will appear when it is viewed from air, vertically above the coin. Draw a suitable ray diagram in support of your answer.
To solve the problem of determining the apparent depth of a coin placed at the bottom of a glass trough containing water, we will use the formula related to the refractive index. Here’s a step-by-step solution:
Step 1: Understand the Given Information
- The refractive index of water (μ) = 43
- The real depth (d) of the water = 20 cm
Step 2: Use the Formula for Refractive Index
The relationship between the real depth (d), apparent depth (h), and refractive index (μ) is given by the formula:
μ=Real DepthApparent Depth
This can be rearranged to find the apparent depth:
Apparent Depth=Real Depthμ
Step 3: Substitute the Values into the Formula
Substituting the known values into the rearranged formula:
h=20cm43
Step 4: Simplify the Calculation
To simplify this, we can multiply by the reciprocal of the refractive index:
h=20cm×34
h=15cm
Step 5: Conclusion
The apparent depth of the coin when viewed from air, vertically above the coin, is 15 cm.
Ray Diagram
To support the answer with a ray diagram:
1. Draw a horizontal line representing the water surface.
2. Mark the real position of the coin at the bottom of the trough (20 cm below the surface).
3. Draw a dashed line to represent the apparent position of the coin (15 cm below the surface).
4. Indicate the direction of light rays bending as they move from water to air.
- The refractive index of water (μ) = 43
- The real depth (d) of the water = 20 cm
The relationship between the real depth (d), apparent depth (h), and refractive index (μ) is given by the formula:
μ=Real DepthApparent Depth
This can be rearranged to find the apparent depth:
Apparent Depth=Real Depthμ
Substituting the known values into the rearranged formula:
h=20cm43
To simplify this, we can multiply by the reciprocal of the refractive index:
h=20cm×34
h=15cm
The apparent depth of the coin when viewed from air, vertically above the coin, is 15 cm.
To support the answer with a ray diagram:
1. Draw a horizontal line representing the water surface.
2. Mark the real position of the coin at the bottom of the trough (20 cm below the surface).
3. Draw a dashed line to represent the apparent position of the coin (15 cm below the surface).
4. Indicate the direction of light rays bending as they move from water to air.
Topper's Solved these Questions
Similar Questions
A coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
View SolutionA coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
View SolutionA plane mirror is fixed at the bottom of a tank containing water. A small object is kept at a height of 24 cm from the bottom and is viewed from a point vertically above it. The distance between the object and the image in the mirror as appears to the person is
View SolutionA coin at the bottom of a trough containing water to a depth of 15 cm appears to be 3.75 cm raised above from the bottom. Calculate the refractive index of water.
View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
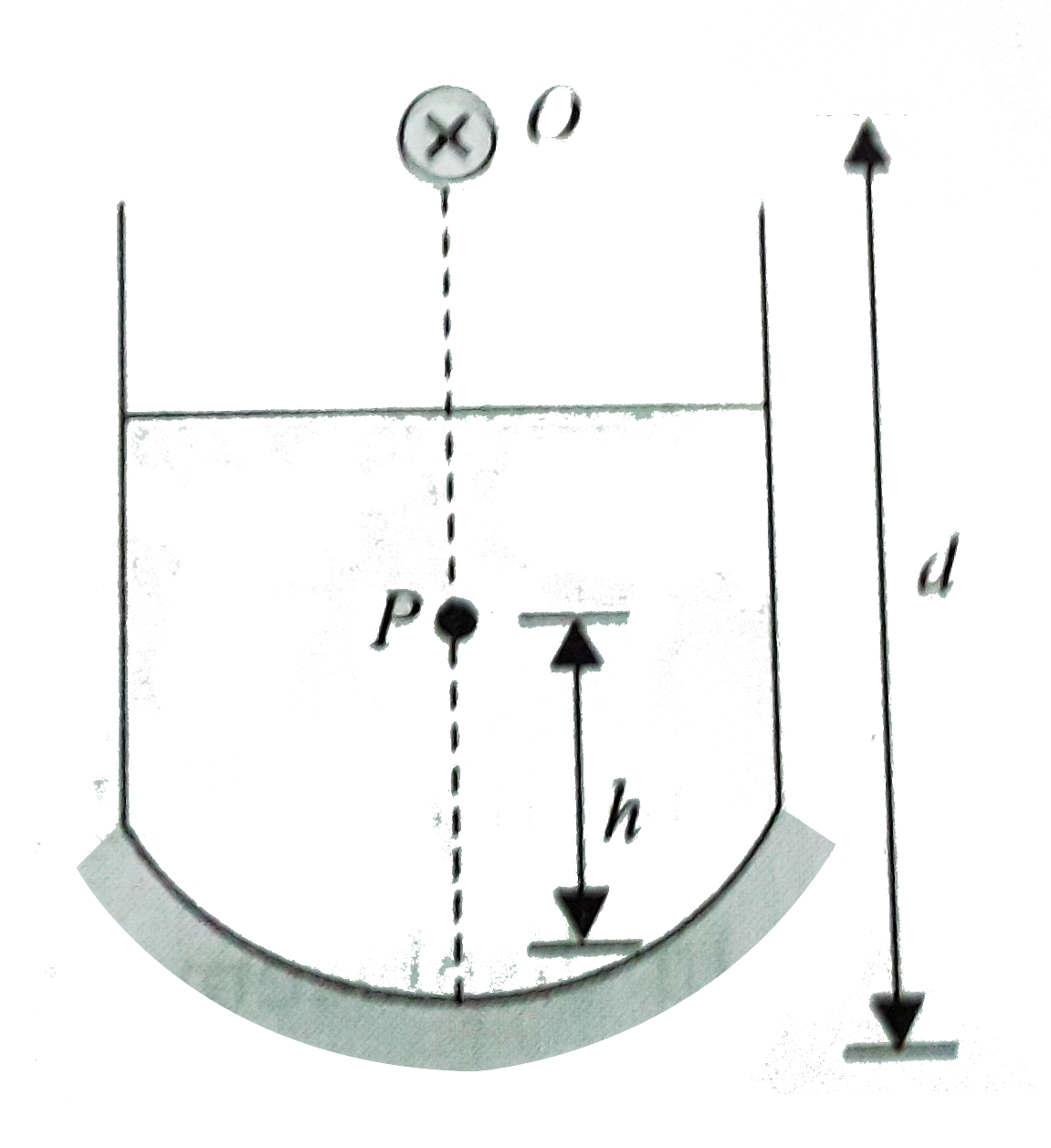
View SolutionA spot is placed on the bottom of a slab made of transperent material of refractive index 1.5. The spot is viewed vertically from the top when it seems to be raised by 2 cm. Then, the height of the slab is
View SolutionA concave mirror of radius of curvature 60 cm is placed at the bottom of tank containing water upto a height of 20 cm. The mirror faces upwards with its axis vertical. Solar light falls normally on the surface of water and the image of the sun is formed. If aμw=43 then with the observer in air, the distance of the image from the surface of water is:
View SolutionA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View SolutionA coin kept inside water (μ=4/3) when viewed from air in a vertical direction, appears to be raised by 2⋅0mm. Find the depth of the coin in water.
View SolutionAn object is placed at 24 cm distant from a surface of a lake. If water has refractive index of 4/3, then at what distance from the lake surface, a fish will get sight of an object.
View Solution
