A coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
Shift = Real depth ×(1−1μ)=16cm
Topper's Solved these Questions
- SELF ASSESSMENT PAPER -2Book:ICSEChapter:SELF ASSESSMENT PAPER -2Exercise:SECTION .B.
Explore 37 Videos
- SELF ASSESSMENT PAPER -1Book:ICSEChapter:SELF ASSESSMENT PAPER -1Exercise:SECTION .B.
Explore 36 Videos
- SELF ASSESSMENT PAPER -3Book:ICSEChapter:SELF ASSESSMENT PAPER -3Exercise:SECTION-B
Explore 42 Videos
Similar Questions
A pond appears to be 2.7 m deep. If the refractive index of water is 43, find the actual depth of the pond.
View SolutionThe refractive index of water is 4/3. The speed of light in water is
View SolutionA water pond appears to be 2⋅7m dep. If the refractive index of water is 4/3, find the actual depth of the pond.
View SolutionThe refractive index of water is 4/3'. Explain the meaning of this statement.
View SolutionBrewster angle for air to water transition is (refractive index of water is 43)
View SolutionWhy is a coin placed in a bowl of water appears raised?
View SolutionA mark at the bottom of a liquid appears to rise by 0.1m. The depth of the liquid is 1m. The refractive index of the liquid is
View SolutionA coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
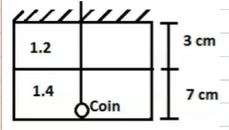
View SolutionA man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
View SolutionA glass slab of thickness 4cm contains the same number of waves as 5cm of water, when both are traversed by the same monochromatic light. If the refractive index of water is 4/3, then refractive index of glass is
View Solution