A man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
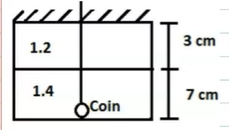
The correct Answer is:8
[8]
d=3.61.2+71.4=8
Similar Questions
A coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
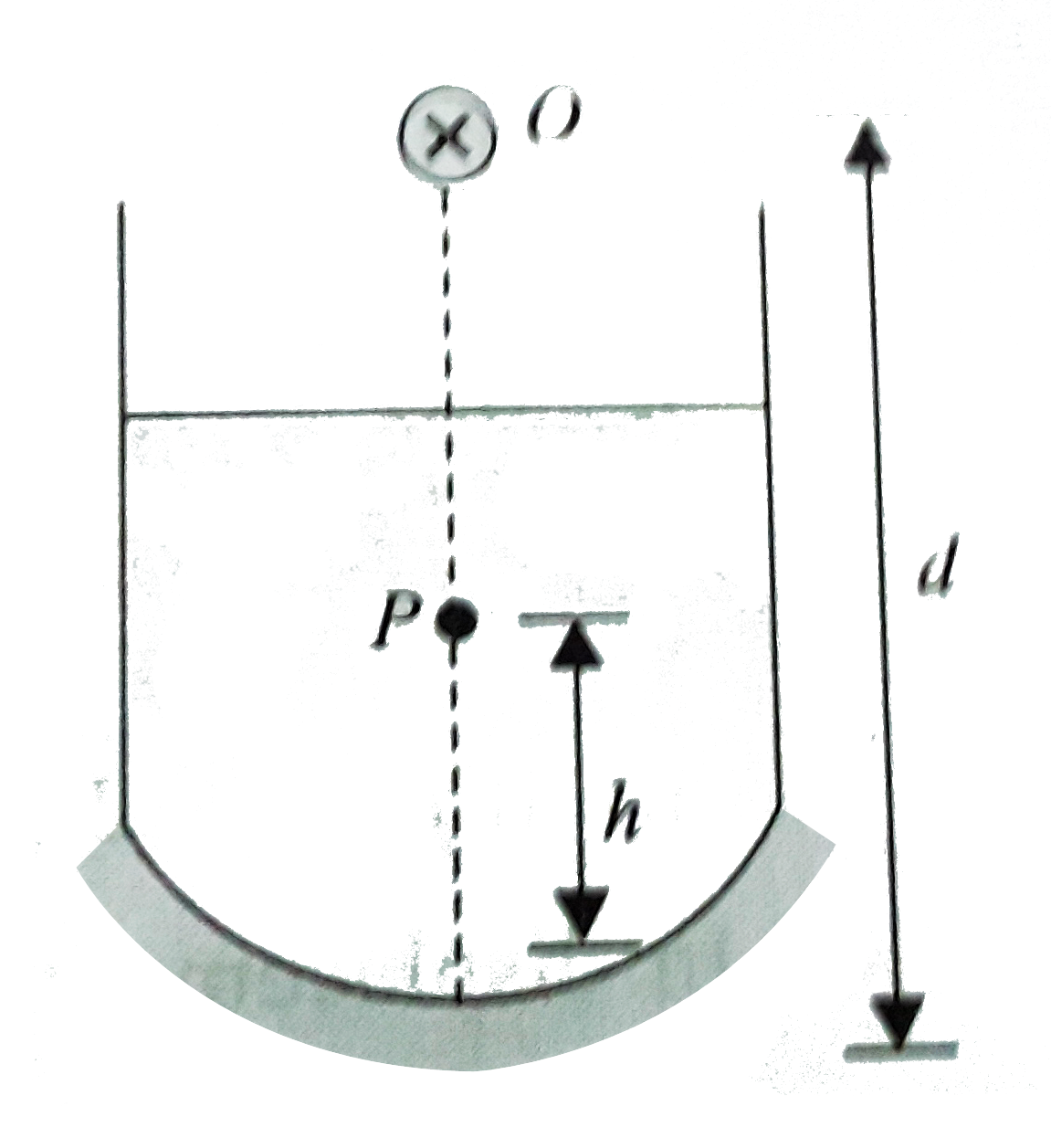
View SolutionA coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
View Solution
Two liquids which do not react chemically are placed in a bent tube as shown in figure. The height of the liquids above their surface of separation are
View SolutionA beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
View SolutionA point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
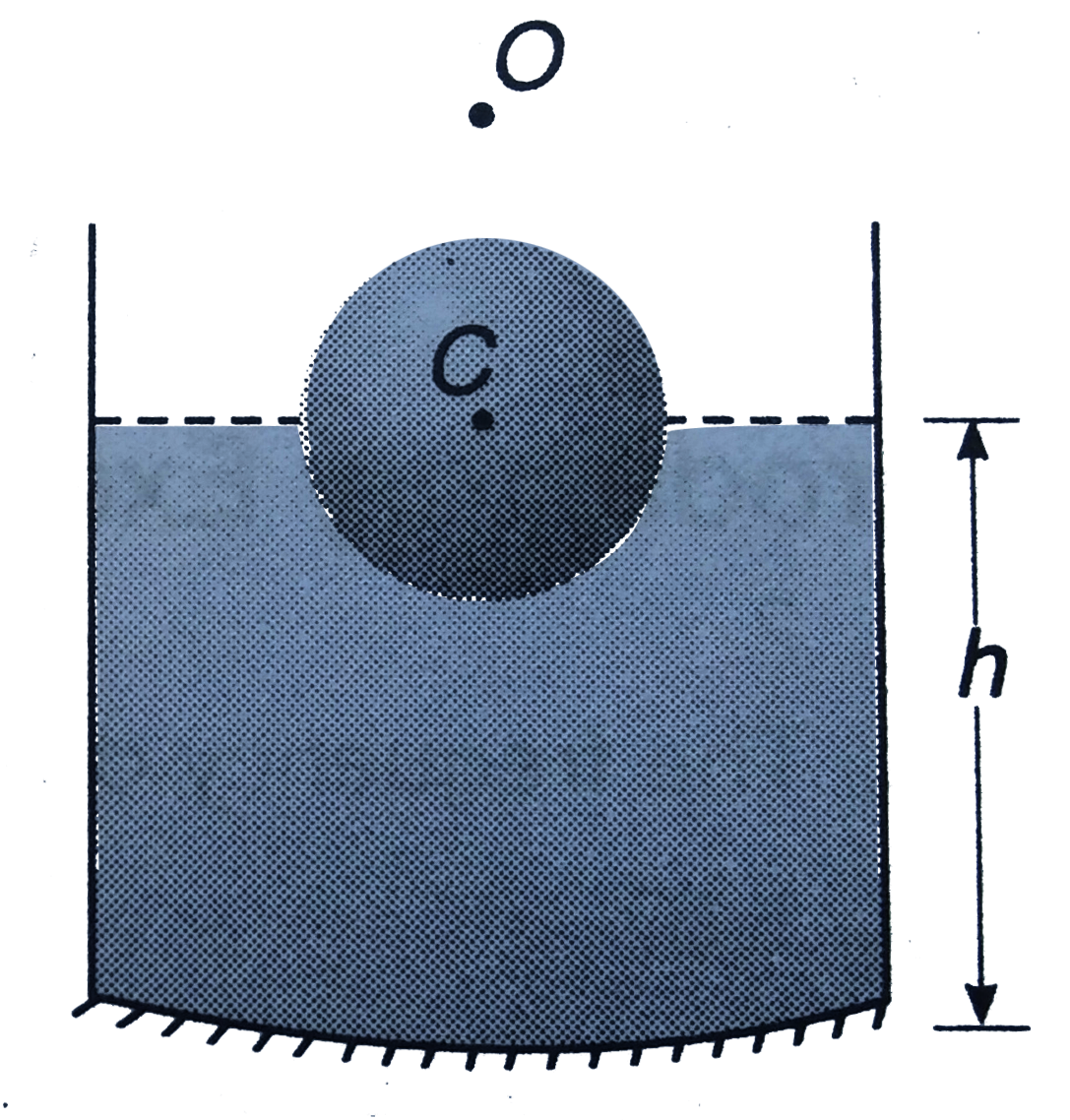
View SolutionA transparent solid sphere of radius 2cm and density ρ floats in a transparent liquid of density 2ρ kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3/2 and that of the liquid is 4/3.
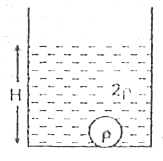
View SolutionA small ball of density ρ is placed from the bottom of a tank in which a non viscous liquid of density 2ρ is filled . Find the time taken by the ball to reach the surface of liquid and maximum height reached above the bottom of container . (Size of the ball and any type of drag force acting on the ball are negligible )
View SolutionA plane mirror is placed at the bottom of a tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observer observes P and its image in the mirror. The apparent distance between two will be
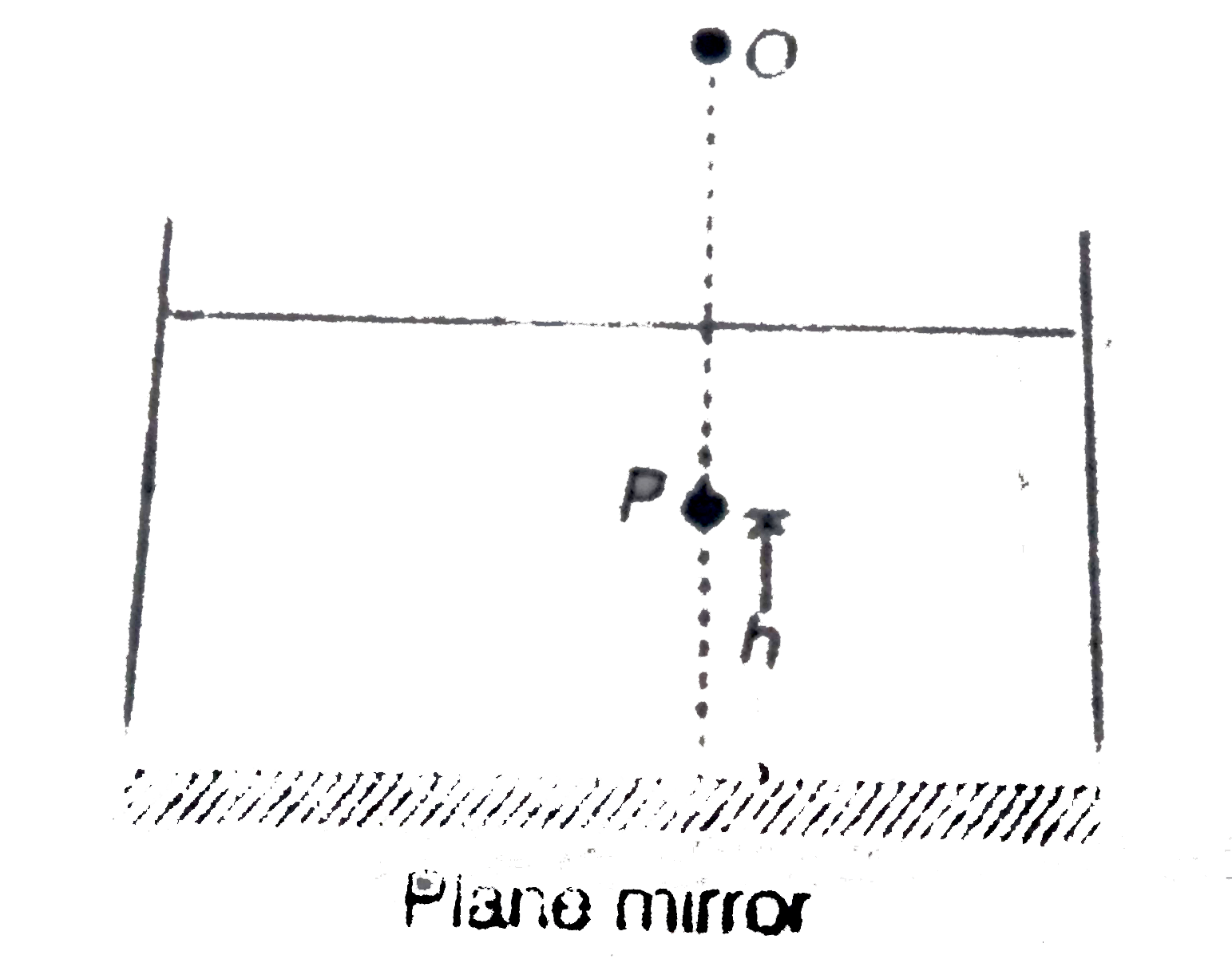
View SolutionA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View Solution