A composite block is made of slabs A,B,C,D and E of different thermal conductivities (given in terms of a constant K and sizes (given in terms of length, L) as shown in the figure. All slabs are of same width. Heat 'Q' flows only from left to right through the blocks. Then in steady state
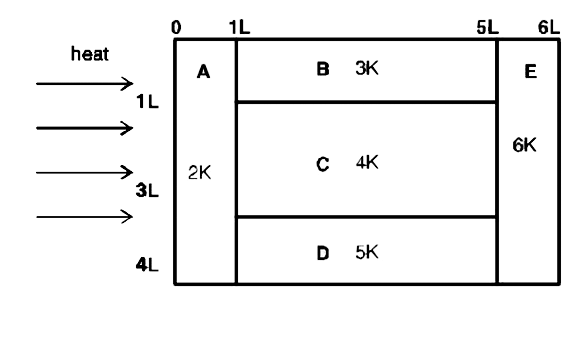
heal flow through A and E slabs are same.
heat flow through slab E is maximum
temperature difference across slab E is smallest.
heat flow through C=heat flow through B + heat flow throughD.
The correct Answer is:A, C, D
(a,c,d)
It is given that heat Q flows only from left to right through
the blocks. Therefore heat flow through A and E slabs are
the same.
∴[a]iscorrectoption<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_HTG_C09_095_S01.pngwh=80%mx-autosty≤=background:white;><br>Sinceheatflowthroughsl|A|andEissame,<br>[b]is¬correct.<br>Weknowtˆresistance→heatflowisR=l/(KA)<br>Letthewhofsl|b|eZ.Then<br>R_A=L/(2K(4L)Z)=1/(8KZ), R_B=(4L)/(3K(LZ))=4/(3KZ)<br>R_C=4L/(4K(2LZ))=1/(2KZ), R_D=(4L)/(5K(LZ))=4/(5KZ)<br>R_E=L/(6K(4LZ))=1/(24KZ)<br>Now,DeltaT=QR<br>AsR_Eis≤∗,DeltaT_Eisalsosmal≤stiesincetheresistance→<br>heatflowis≤∗forslabE,thetemperatured⇔erenceacross<br>issmal≤st.<br>:. Option (c) is the correct answer.
Also
QC=ΔTCRC=ΔTC1/2KZ=2KZ(ΔTC)<br>Q_B=(DeltaT_B)/(R_B)=(DeltaT_C)/(4//3KZ)=(3KZ(DeltaT_C))/4 [:' DeltaT_B=DeltaT_B]<br>Q_D=(DeltaT_D)/(R_D)=(DeltaT_C)/(4//5KZ)=(5KZ(DeltaT_C))/4 [:' DeltaT_D=Delta_C]<br>Q_B+Q_D=(3KZ(DeltaT_C))/4+(5KZ(DeltaT_C))/4<br>=(8KZ(DeltaT_C))/4=2KZ(DeltaT_C)=QC<br>:. (d) is the correct option.
Topper's Solved these Questions
Similar Questions
Three blocks A,B and C of mass m,m2 and m of different densilties and dimensions are placed over each other as shown in the figure. The cofficients of friction are shown. Blocks placed in a vertical line are mae to over towards right with same velcity at the same instant. Find the time (in sec) taken by the upper block A to topple from the middle blcok B. Assume that blocks B and C don't stop sliding before A topples from B. (given L=36m,μ=0.4 and g=10m/s2)

View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
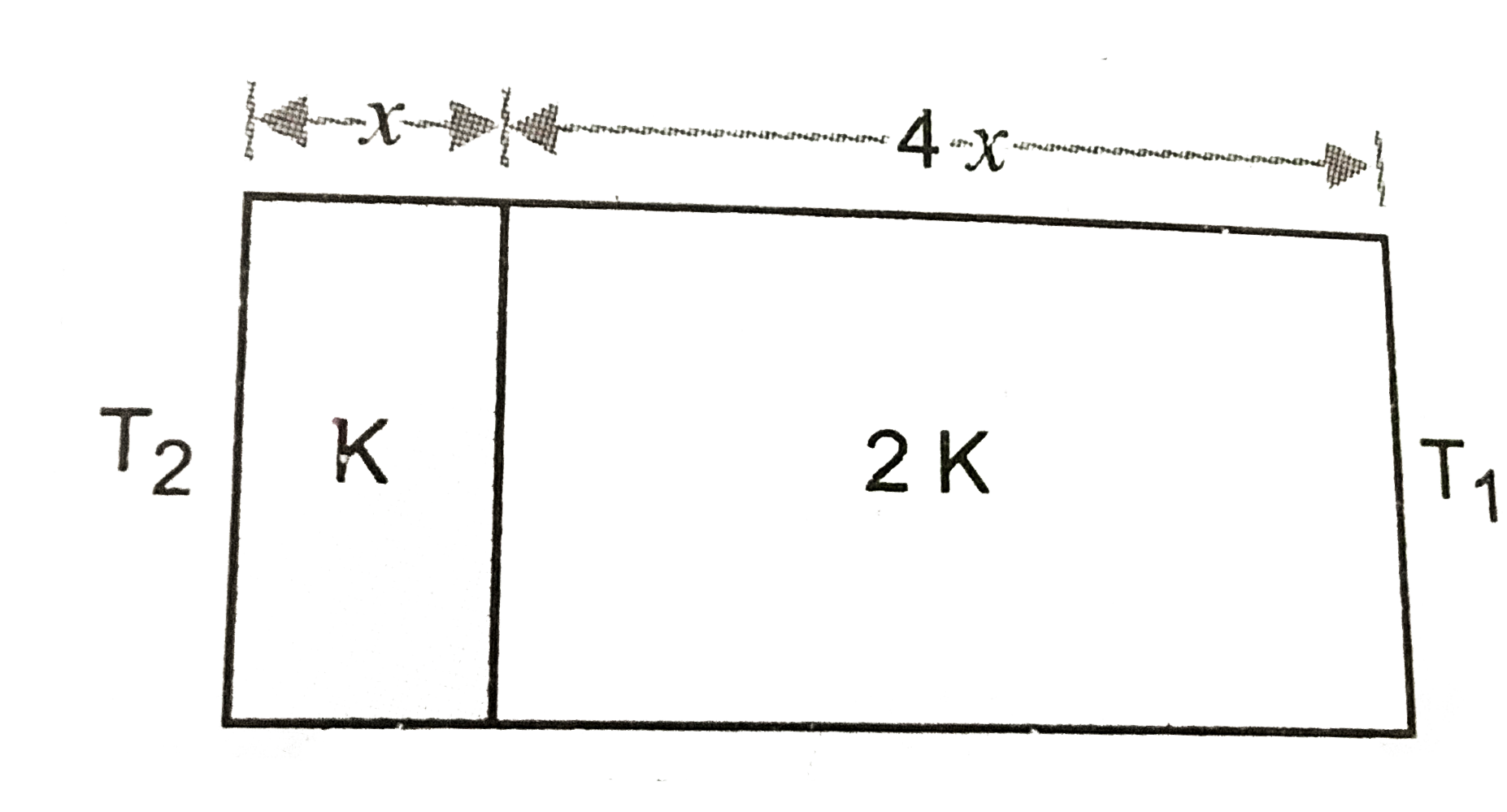
View Solution
Knowledge Check
A composite rod made of three rods of equal length and cross-section as shown in fig. The thermal conductivites of the materials of the rods are K/2, 5K and K respectively. The end A and end B are at constant tempertures. All heat entering the face A goes out of the end B there being no loss of heat from the sides of the bar. The effective thermal conductivity of the bar is
 A15K/16B6K/13C5K/16D2K/3
A15K/16B6K/13C5K/16D2K/3Two bars of equal length and the same cross-sectional area but of different thermal conductivities,k1 and k2, are joined end to end as shown in figure-4.36. One end of the composite bar is maintained at temperature Th whereas the opposite end is held at Tc.
If there are no heat losses from the sides of the bars, the temperature Tj of the junction is given by :
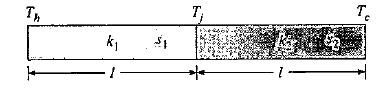 Ak2k1(Th+Tc)2Bk2k1+k2(Th+Tc)Ck1+k2k2(Th+Tc)2D1k1+k2(k1Th+k2Tc)
Ak2k1(Th+Tc)2Bk2k1+k2(Th+Tc)Ck1+k2k2(Th+Tc)2D1k1+k2(k1Th+k2Tc)A parallel-sided slab is made of two different materials. The upper half of the slab is made of material X, of thermal conductivity λ, the lower half is made of material Y, of thermal conductivity 2λ. In the steady state, the left hand face of the composite slab is at a higher, uniform temperature than the right-hand face, and the flow of heat through the slab is parallel to its shortest sides. What fraction of the total heat flow through the slab passes through material X ?
A14B13C12D23
Figure shows the cross section of a wall made of white pine of thickness La and brick of thickness Ld==2.0La , sandwiching two layers of unknonw material with identical thicknesses and thermal conductivities. The thermal conductivity of the pine is ka and that of the brick is kd(=5.0ka). The face area A of the wall is unknown. Thermal conduction through the wall has reached the steady state, the only known interface temperatures are T1=25∘C,T2=20∘C, and T5=−10∘C. What is interface temperature T4 ?
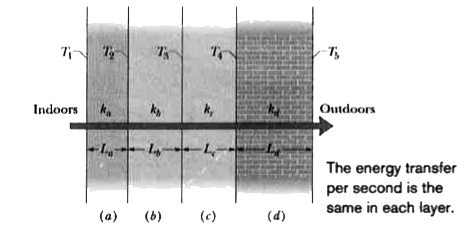
View SolutionA rod AB of uniform cross-section consists of 4 sections AC, CD, DE and EB of different metal with thermal conductivities K, 0.8,1.2K and 1.5 respectively. Their lengths are respectively L,1.2L,1.5L and 0.6L. They are jointed rigidly in Succession at C, D and E to from the rod AB The end A is mainained at 100∘C and the end B is the maintained at 0∘C. The steady state temperatures p the joints C, D and E are respectively TC,TD and TE Match the following two columns
View SolutionA composite cylinder is made of two materials having thermal conductivities K1 and K2 as shown. Temperature of the two flat faces of cylinder are maintained at T1 and T2. For what ratio K1/K2 the heat current throught the two materials will be same. Assume steady state and the rod is lagged (insulated from the curved surface).
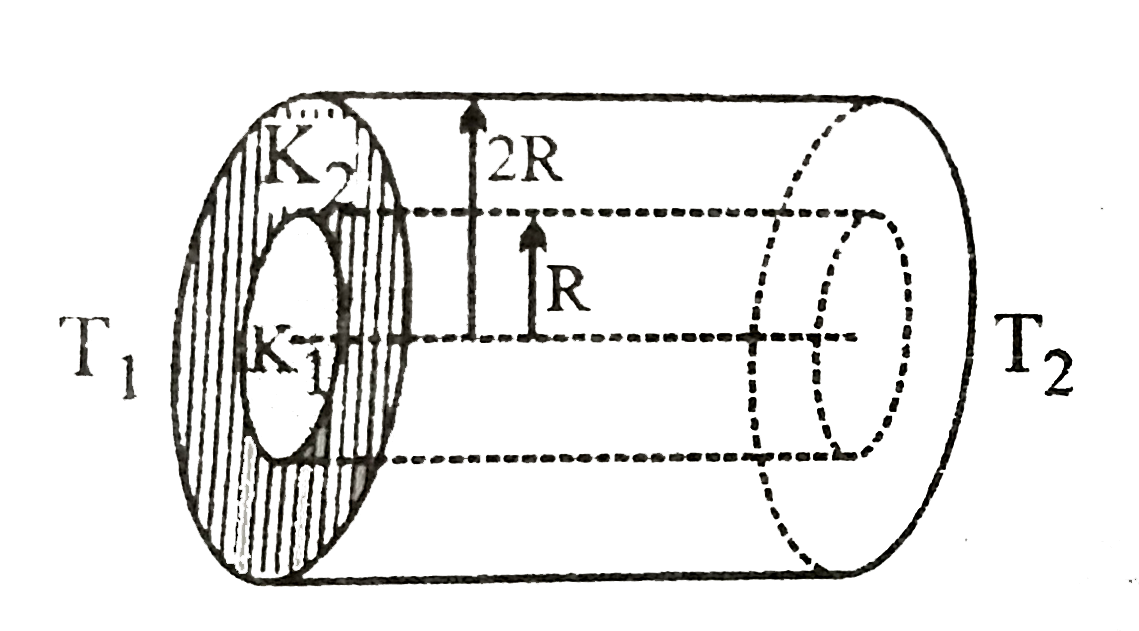
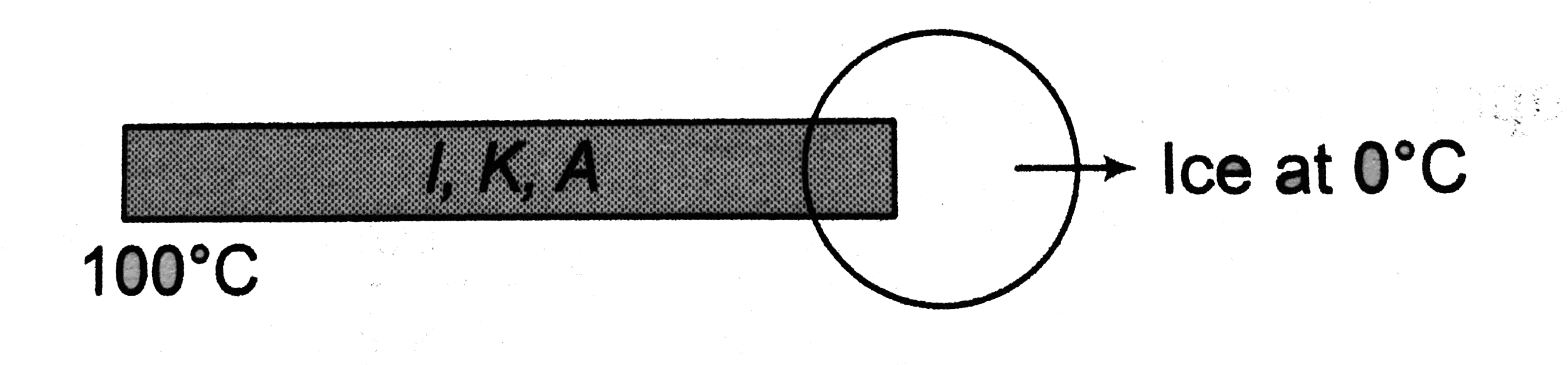
View SolutionOne end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
 .
.
View SolutionA wall consists of alternating blocks withlength 'd' and coefficient of thermal conductivity k1 and k2. The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is:-

View Solution
