A conducting rod (OP) of length L rotates in form of a conical pendulum with an angular velocity ω about a fixed vertical axis passing through its end O. There is a uni- form magnetic field B in vertically downward direction. The rod makes an angle θ with the direction of the magnetic field. Calculate the emf induced across the ends of the rod. Which end is positive?
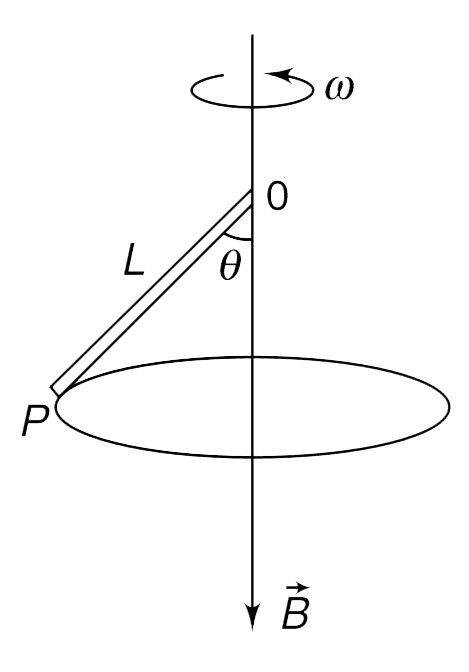
The correct Answer is:12BωL2sin2θ;O is positive
Step by step video, text & image solution for A conducting rod (OP) of length L rotates in form of a conical pendulum with an angular velocity omega about a fixed vertical axis passing through its end O. There is a uni- form magnetic field B in vertically downward direction. The rod makes an angle theta with the direction of the magnetic field. Calculate the emf induced across the ends of the rod. Which end is positive? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- CURRENT ELECTRICITYBOOK - ARIHANTCHAPTER - CURRENT ELECTRICITYEXERCISE - Current Electricity
105 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
Similar Questions
Uniform magnetic field B, exists in the vertical downward direction. A rod whose length is kept horizontal and is moved with velocity v perpendicular to its length. Motional emf developed across the length of the rod is
View SolutionA thin uniform conducting rod of mass M and length L oscillates in a vertical plane about a fixed horizontal axis passing through its top end. The rod is oscillating with angular amplitude θ0. A uniform horizontal magnetic field B, perpendicular to the plane of the oscillation is switched on.
(a) Calculate the maximum emf induced between the ends of the rod.
(b) If the rod has a finite thickness (any real life rod will definitely have a thickness), what difference in oscillation is expected in absence of magnetic field and in presence of magnetic field. Describe qualitatively.
View Solution
Knowledge Check
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A rod of length L rotates in the form of a conical pendulum with an Angular velocity ω about its axis as shown in Fig. 3.165. The rod makes an angle θ with the axis. The magnitude of the motional emf developed across the two emf of the rod is
 A(a) 12BωL2B(b) 12BωL2tan2θC( c) 12BωL2cos2θD(d) 12BωL2sin2θ
A(a) 12BωL2B(b) 12BωL2tan2θC( c) 12BωL2cos2θD(d) 12BωL2sin2θA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA metal rod of length 15×10−2m rotates about an axis passing through one end with a uniform angular velocity of 60 rad s−1. A uniform magnetic field of 0.1 Tesla exisits in the direction of the axis of rotationn. Calculate the EMF induced between the ends of the rod.
View SolutionA uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
View Solution
