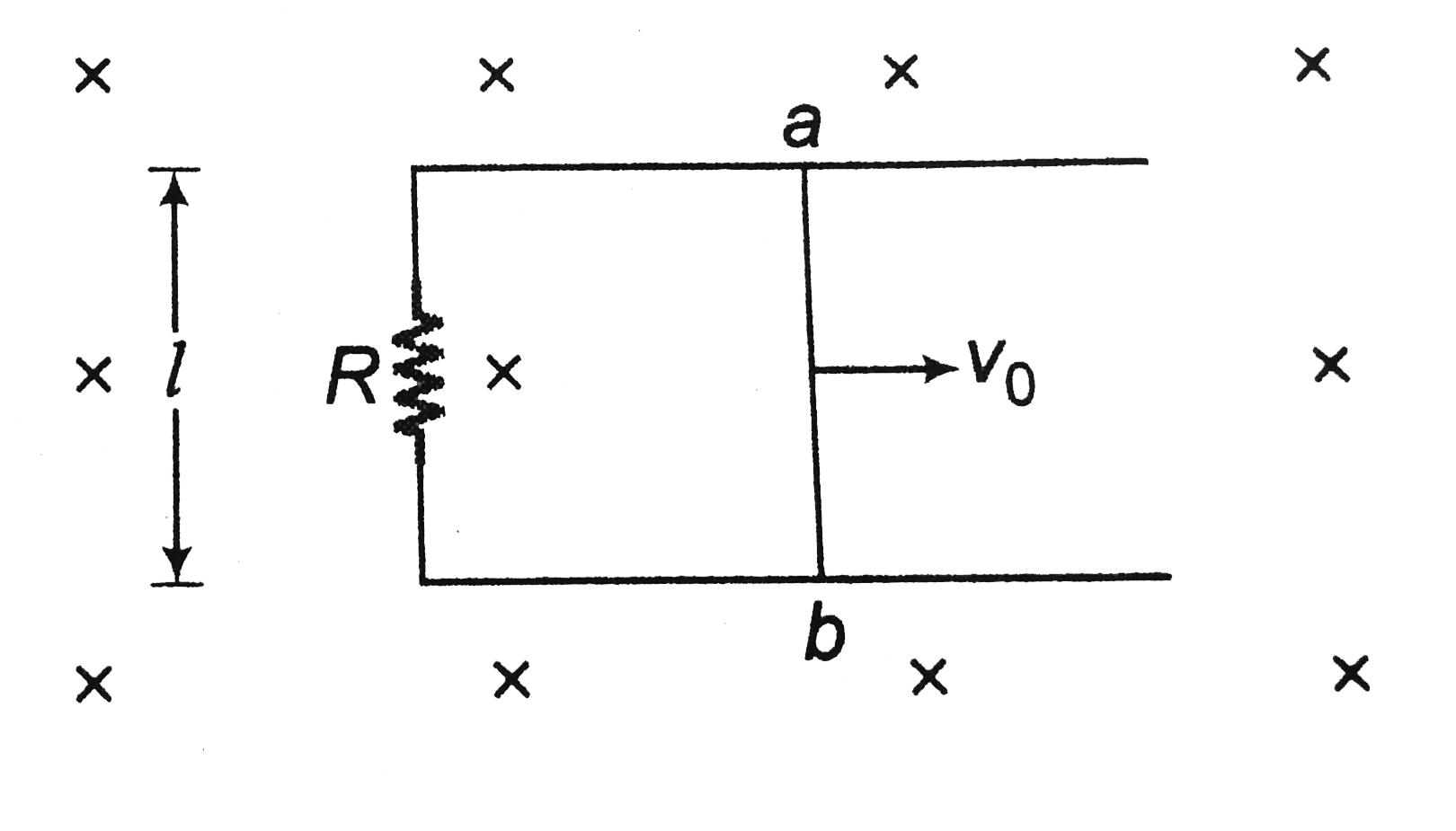
A conducting rod shown in figure of mass m and length l moves on two frictionless horizontal parallel rails in the presence of a unifom magnetic field directed into the page., The rod is given an initial velocity v0 to the right and is released at t=0. Find s a function of time
a. the volocity of the rod
b. the induced current and
c. the magntitude of the induced emf.
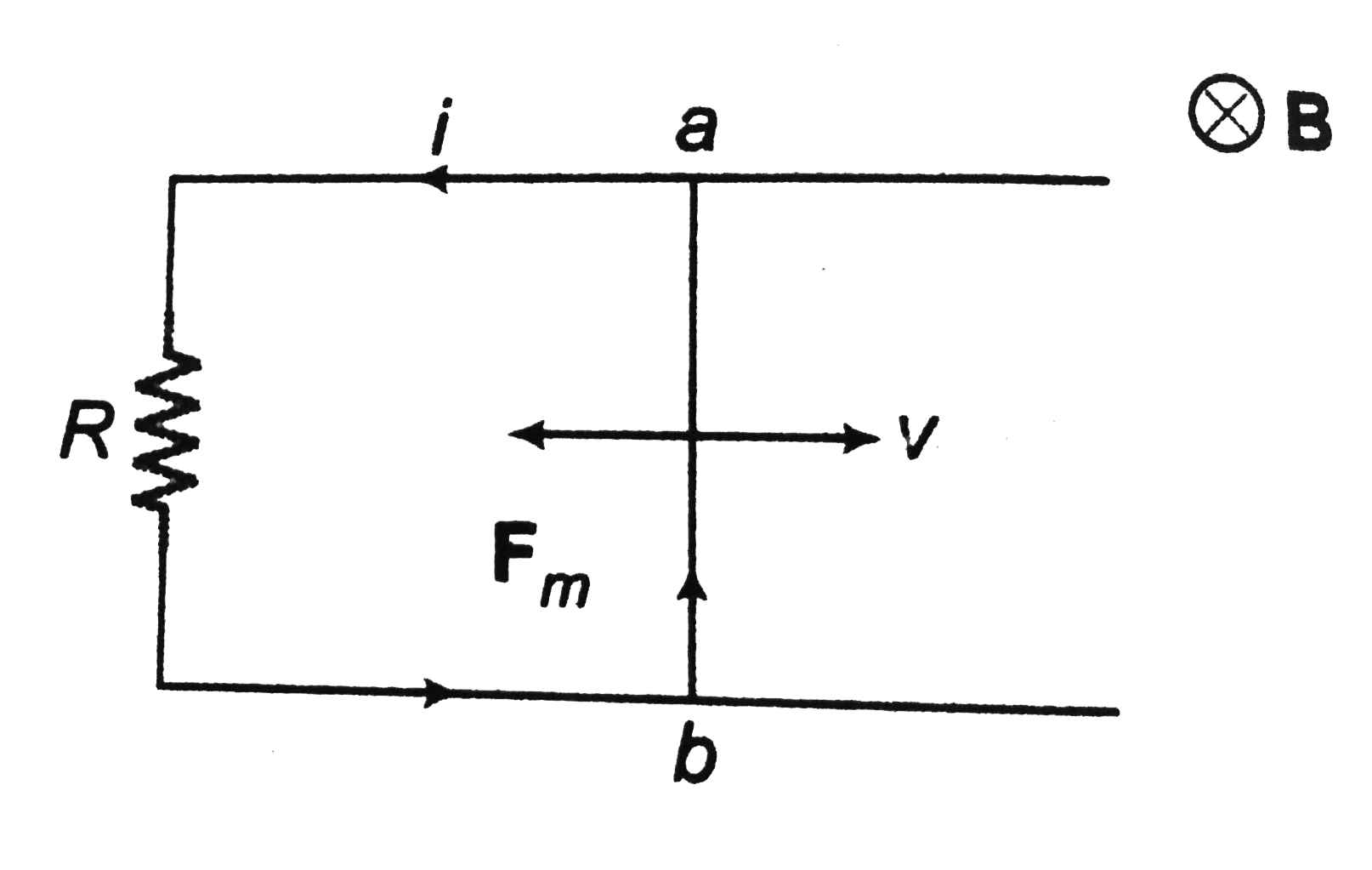
a. Let v be the velocity of the rod at time t
current in the ciruit at his moment is
i=BvlR …..i
From right had rule, we can see that this current is in counterclockwise direction.
The magnetic force is
Fm=−ilB=−B2l2Rv
Hence, negative sign denotes that the force is to the left and retards the motion. This is the only horizontal force acting on the bar, and hence, Newton's second law applied to motion is horizontal direction gives
mdvdt=Fm=−B2l2Rv
∴dvv=−(B2l2mR)dt
Integrating this equation using the initial condition that
v=v0 at t=0, we find that
∫vv0dvv=B2l2mR∫t0dt
Solving this equation we find that
v=v0e−t/τ ...........ii
where ,τ=mRB2l2
This expression indicates that the velocity of the rod decreses expnentially with time under the action of the magnetic retarding force.
b. i=Bvlr
substituting the value of v from Eqn (ii), we get
i=Blv0Re−t/τ
c. eiR=Blv0e−t/τ
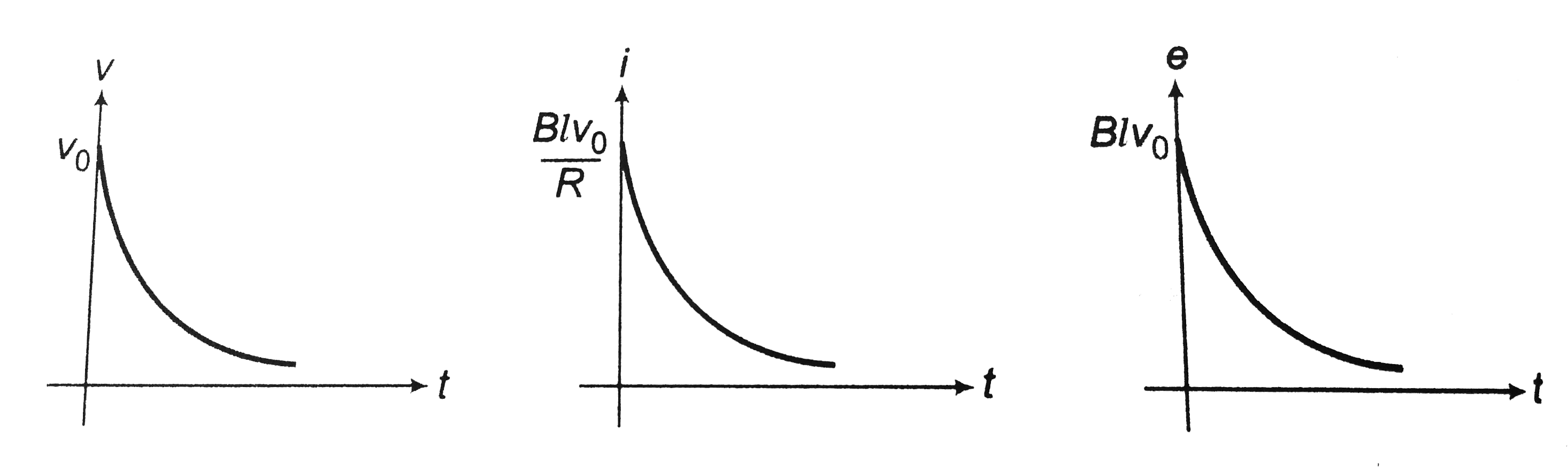
i. and e both decrease exonentially with time v-t, i=t and e-t graphs are as shown in figure.
Alternate solution: This problem can also be solved by energy conservation principle. Let at some instant velocity of the rod is v. As no external force is present. Energy is dissipated in the resistor at the cost of kinetic energy of the rod. Hence,
(−dKdt)= power dissipated in the resistor
or −ddt(12mv2)=e2R
or −mv(dvdt)=B2l2v2R (as e=Bvl)
∴dvv=B2l2mRdt
∴∫vv0dvv=B2l2mRdt
or v=v0e−t/τ, where τ=mRB2l2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.1
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.2
4 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 6
3 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A proton is moving along the negative direction of X-axis in a magnetic field directed along the positive direction of Y-axis. The proton will be deflected along the negative direction of
View SolutionA conducting rod of mass m and length l is placed over a smooth horizontal surface. A uniform magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed through the rod and it acquires an initial velocity v on the surface, then q is equal to
View SolutionA glass rod of length l moves with velocity v in a uniform magnetic field B. What is the e.m.f induced in the rod?
View SolutionA rod of mass m, length l and resistance R is sliding down on a smooth inclined parallel rails with a cinstant velocity v. If a uniform horizontal magnetic field B exists, then find thevalue of B.
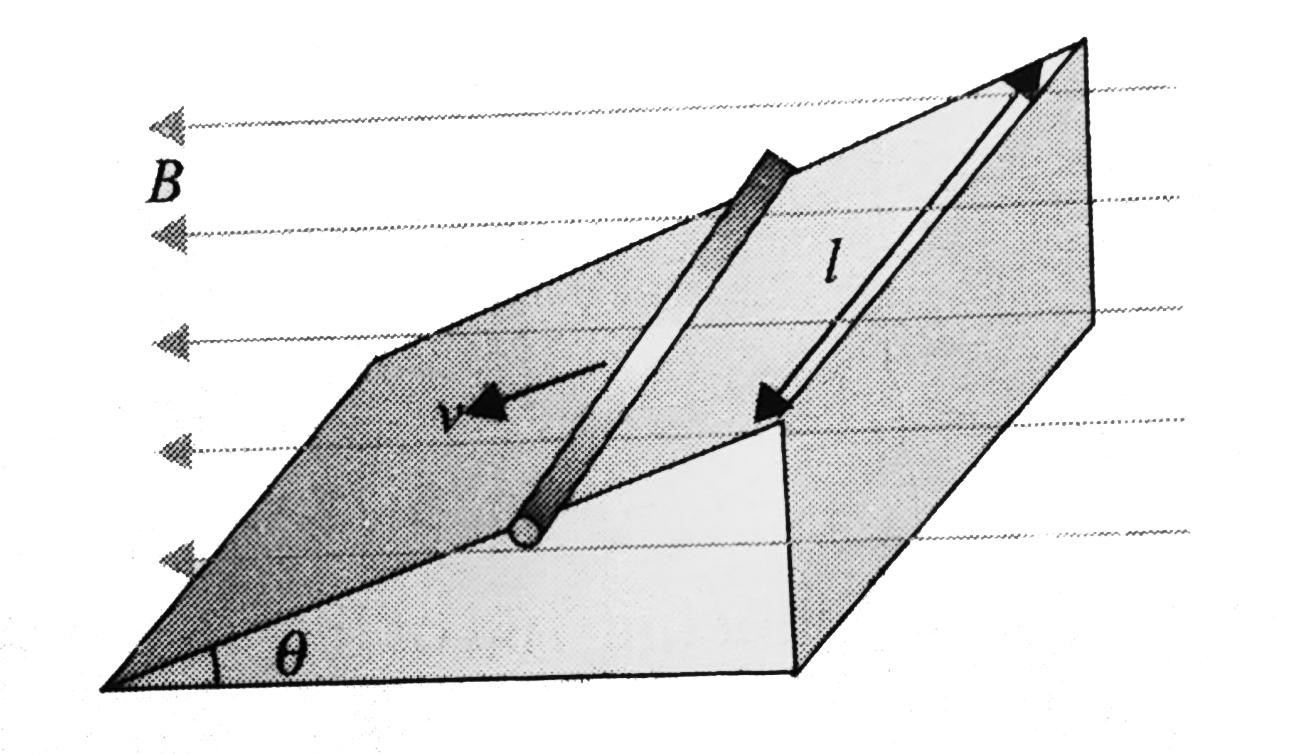
View SolutionA conducting rod of length l falls verticaly under gravity in a region of uniform magnetic field B. The field vectors are inclined at an angle θ with the horizontal as shown in figure. If the instantaneous velocity of the rod is v, the induced emf in the rod ab is
View SolutionA conducting rod PQ of length l=1.0m is moving with a uniform speed v2.0m/s in a uniform magnetic field B=4.0T directed into the paper.
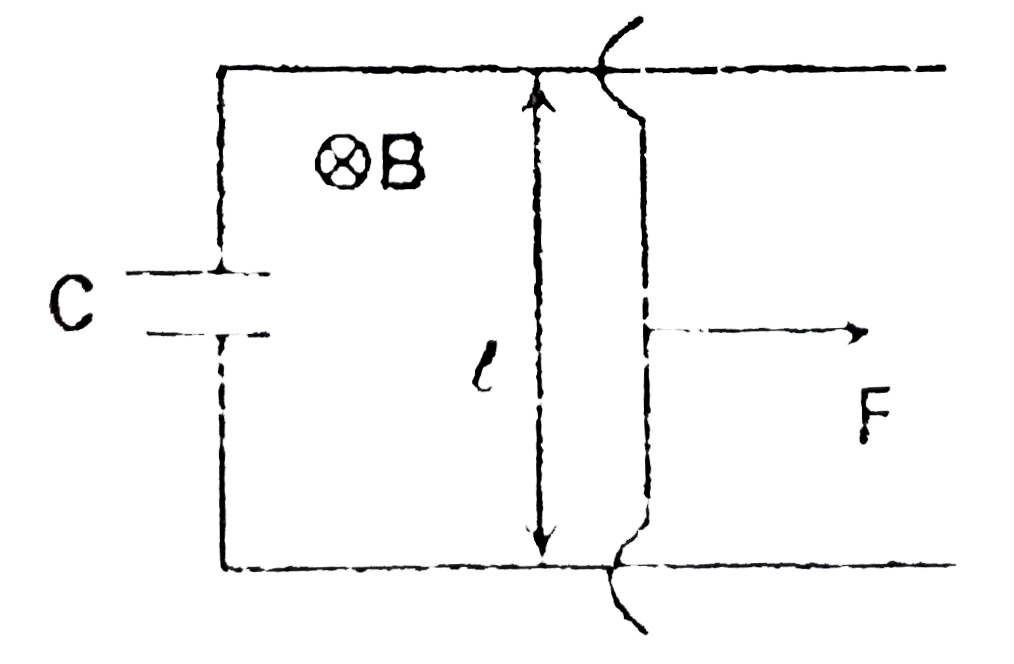
A capacitor of capacity C=10μF is connected as shown in figure. Then

View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View SolutionA conducting rod AB of length l is projected on a frictionless frame PSRQ with velocity v0 at any instant. The velocity of the rod after time t is
View SolutionA conducting rod AB of length l is rotated about point O with an angular velocity velocity omega in a uniform magnetic field (B_0) directed perpendicular into the plane of rotation as shown in the figure. The value of VB−VA is
View Solution
